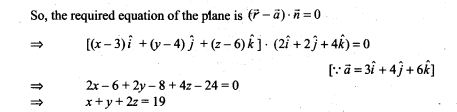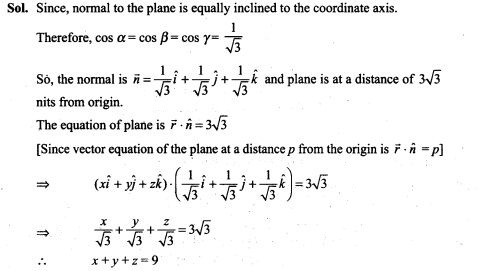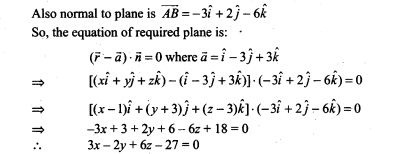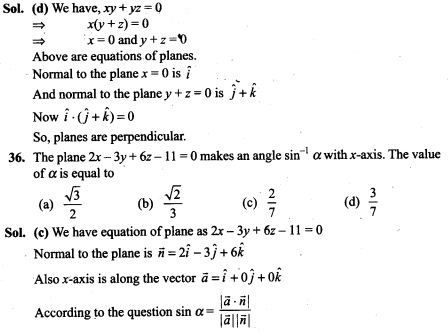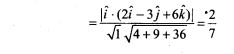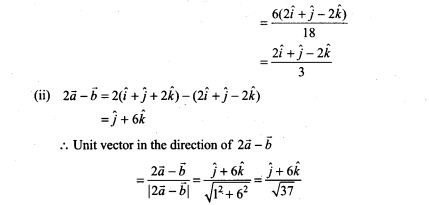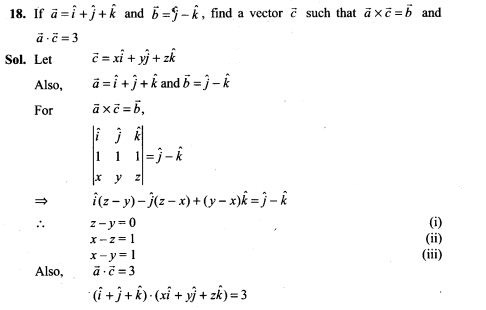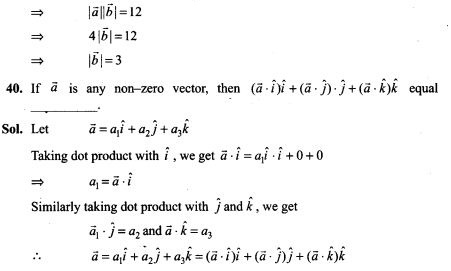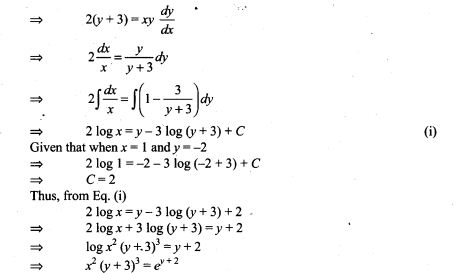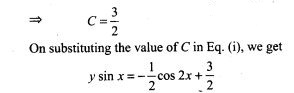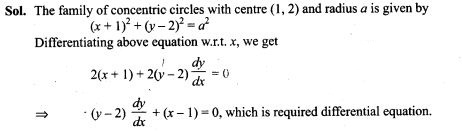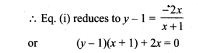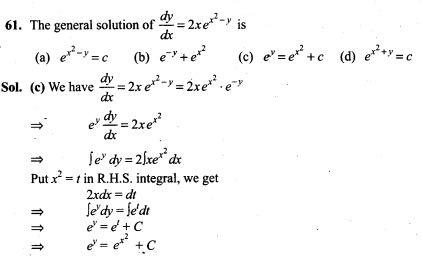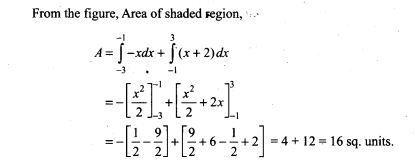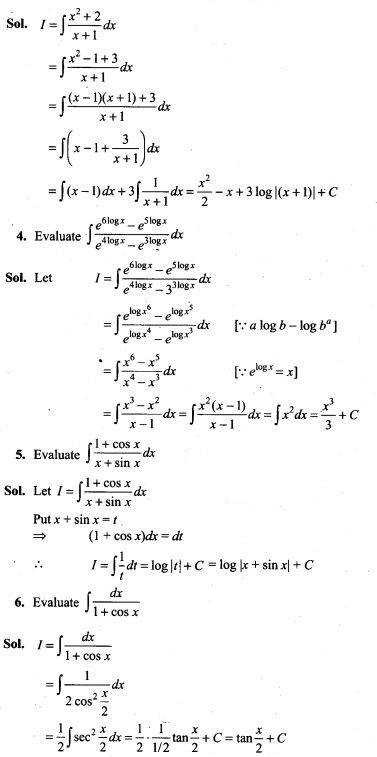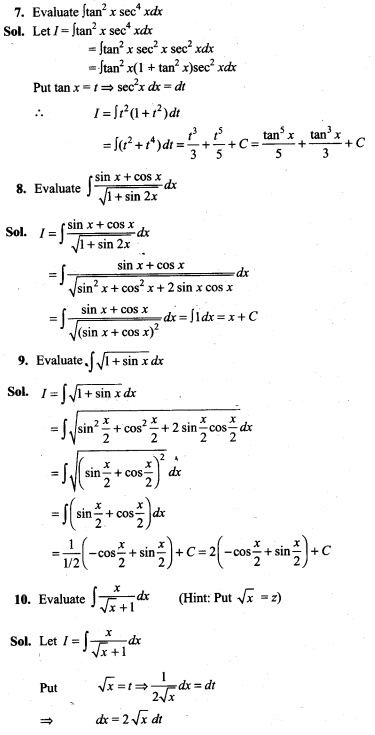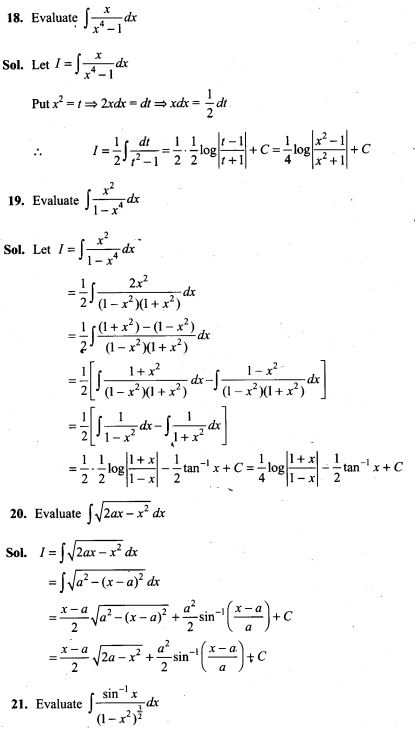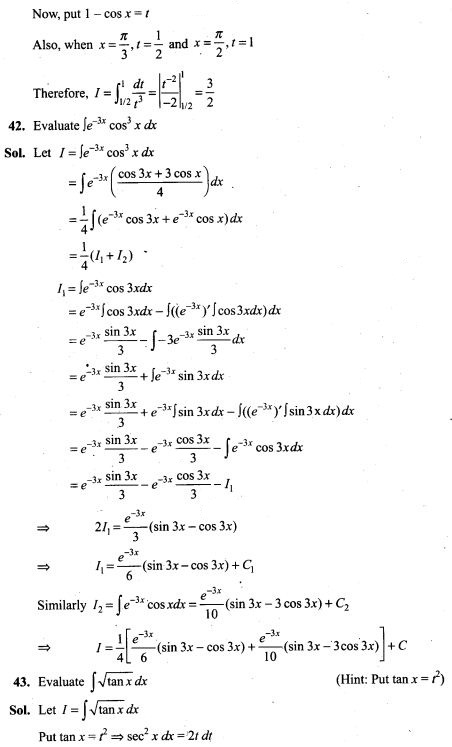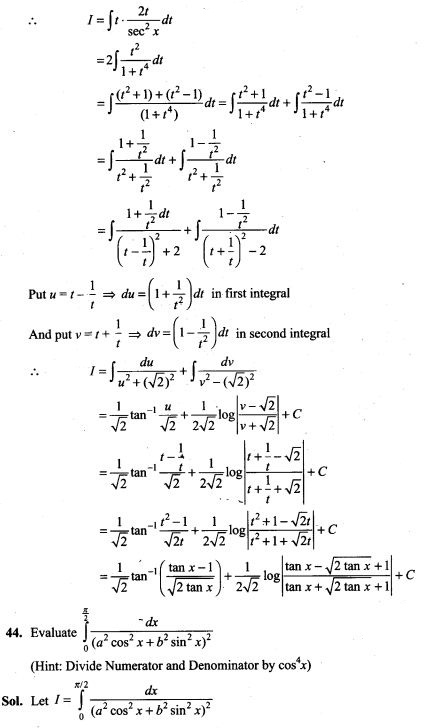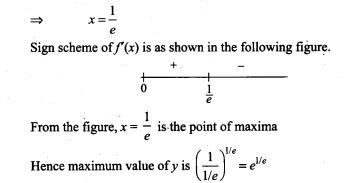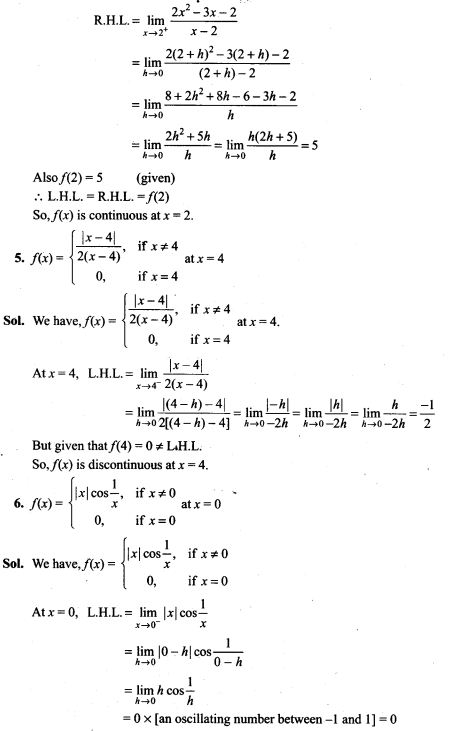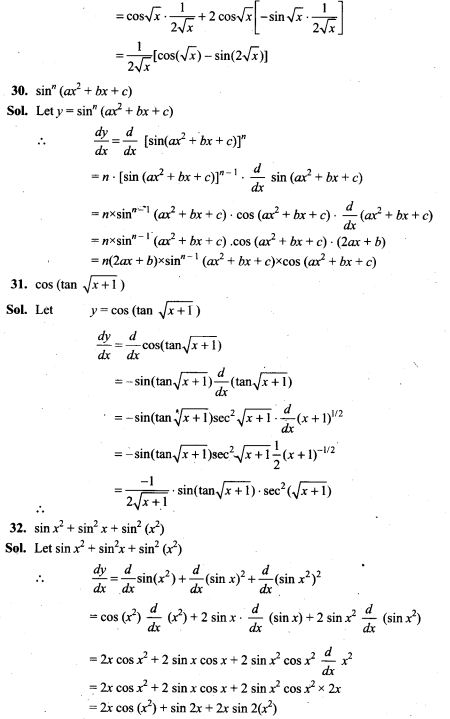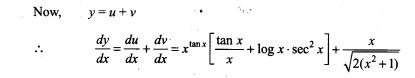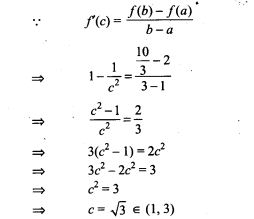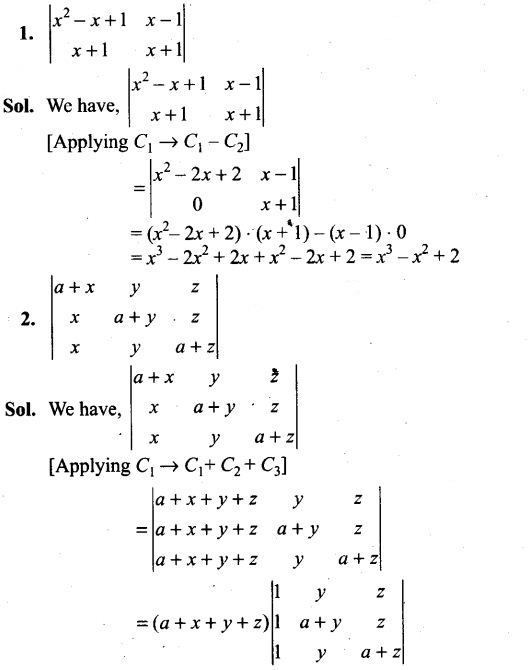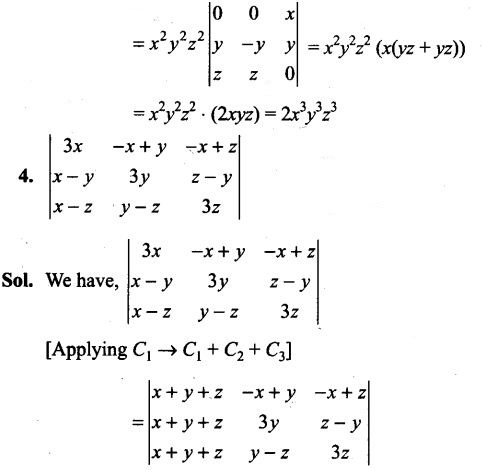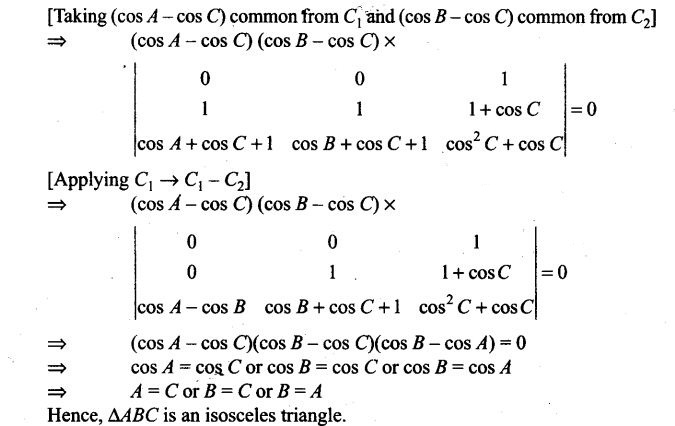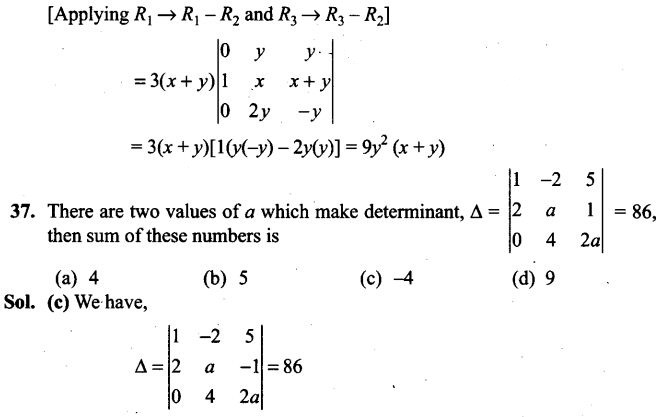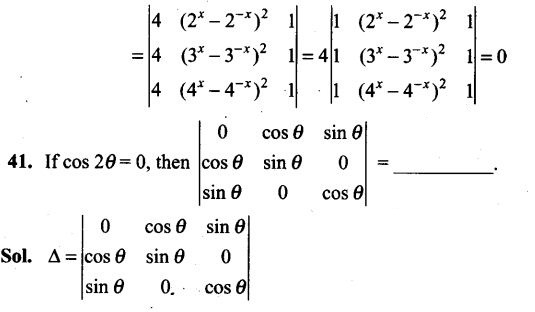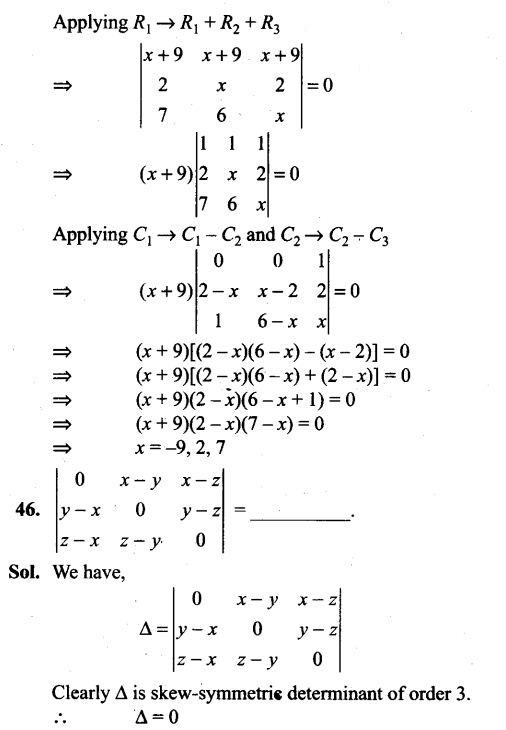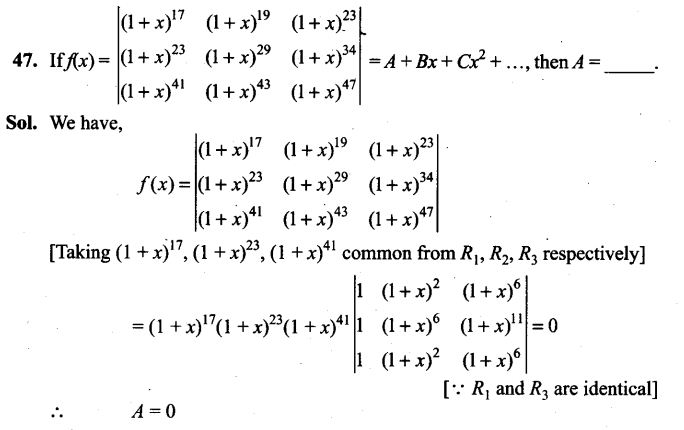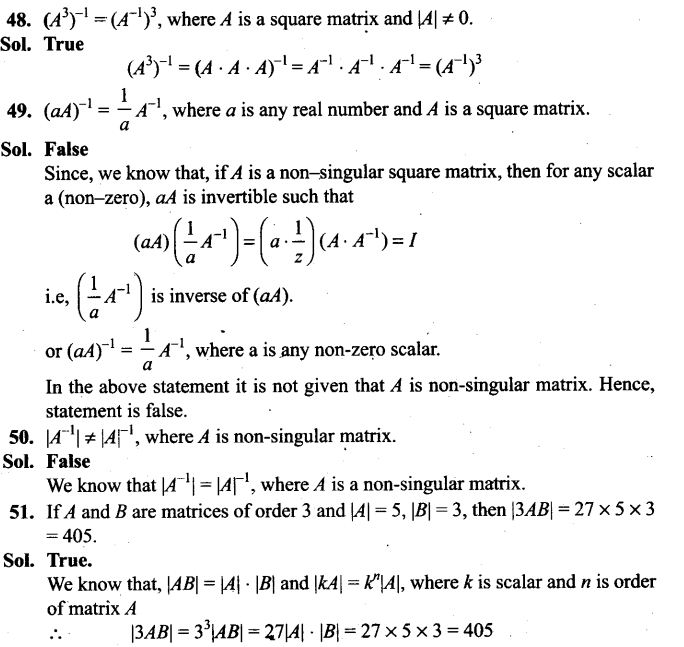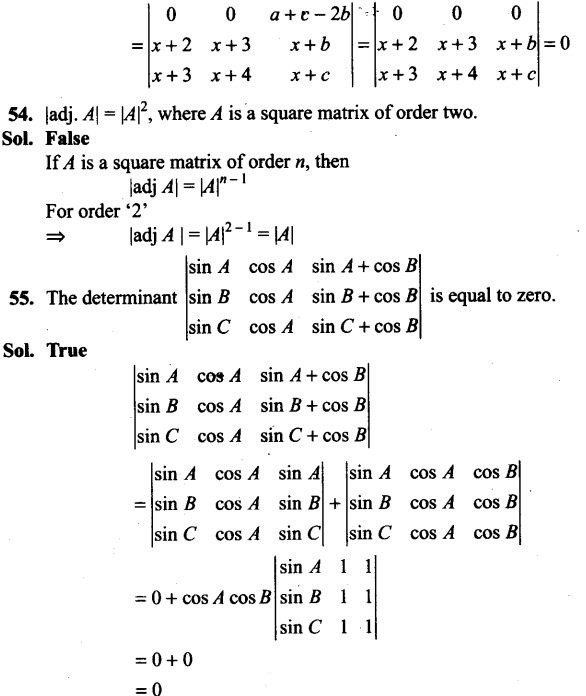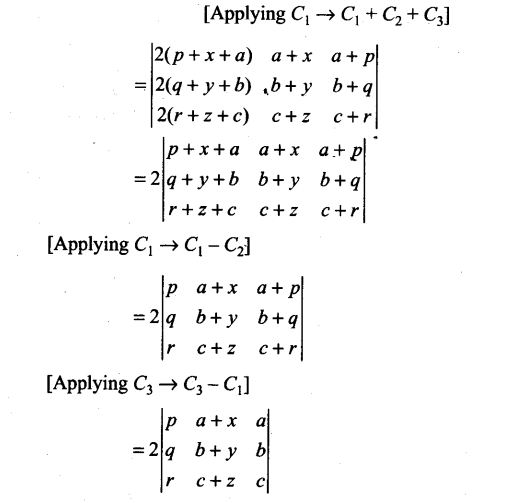Category: Class 12th

NCERT Exemplar Problems Class 12 Mathematics Chapter 13 Probability

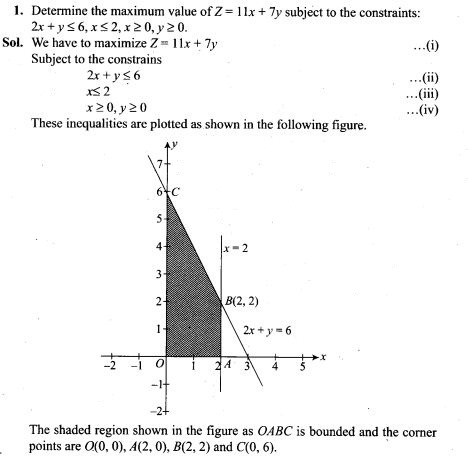
Short Answer Type Questions
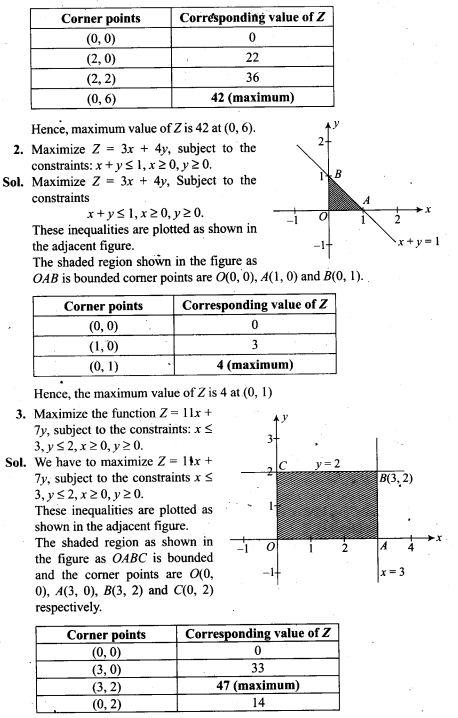
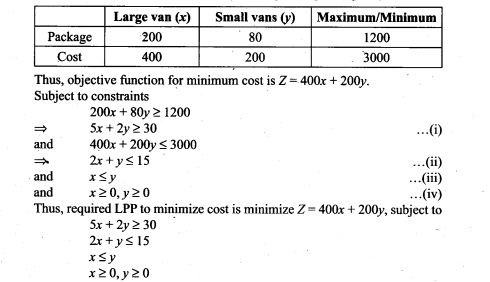
1. For a loaded die, the probabilities of outcomes are given as under:
P(1) = P(2) = 0.2, P(3) = P(5) = P(6) = 0.1 and P(4) = 0.3.
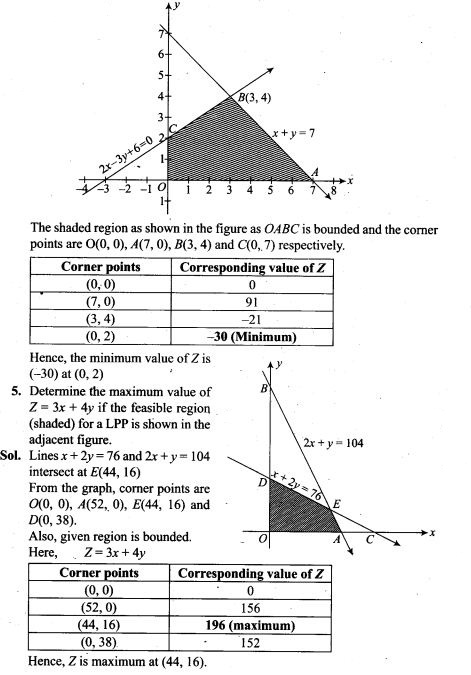
The die is thrown two times. Let A and B be the events, ‘same number each time’, and ‘a total score is 10 or more’, respectively. Determine whether or not/l and B are independent.


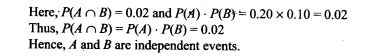
2. Refer to Exercise 1 above. If the die were fair, determine whether or not the events A and B are independent.


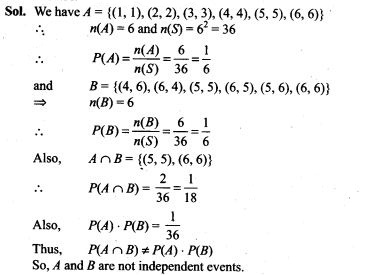
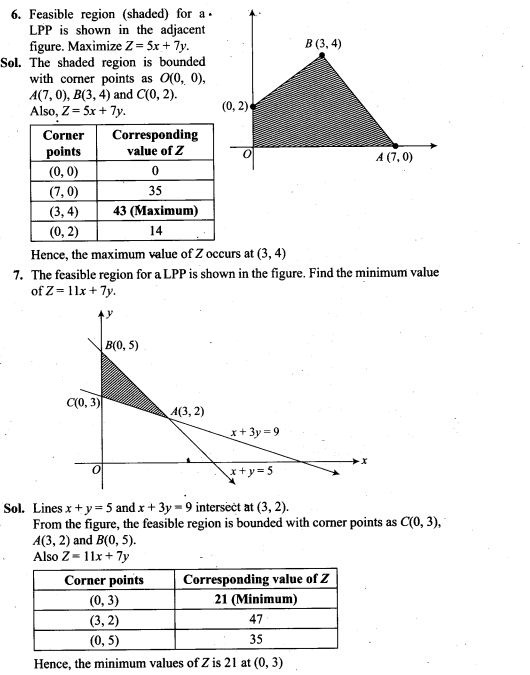
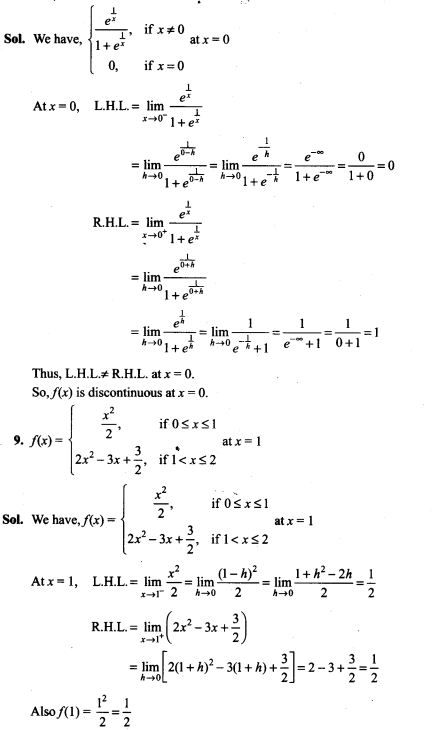
4. A bag contains 5 red marbles and 3 black marbles. Three marbles are drawn one by one without replacement. What is the probability that at least one of the three marbles drawn be black, if the first marble is red?


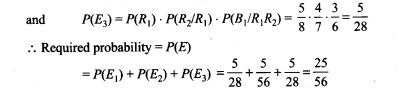
5. Two dice are thrown together and the total score is noted. The events E, F and G are ‘a total of 4’, ‘a total of 9 or more’, and ‘a total divisible by 5’, respectively. Calculate P(E), P(F) and P(G) and decide which pairs of events, if any, are independent.

6. Explain why the experiment of tossing a coin three times is said to have binomial distribution.
Sol. We know that, in a Bindmial distribution,
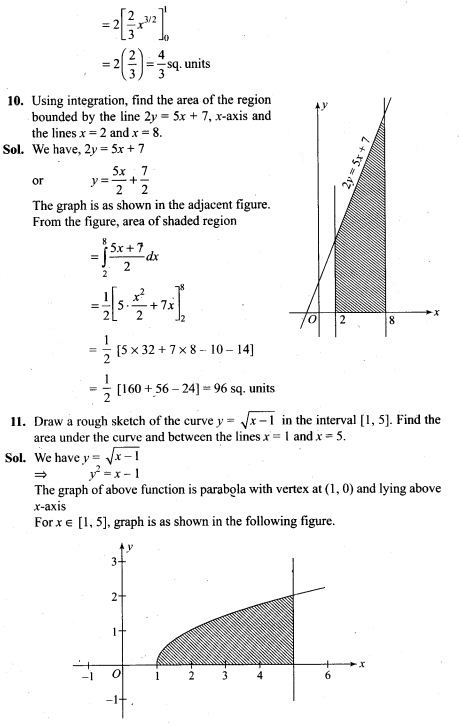
(i) There are 2 outcomes for each trial
(ii) There is a fixed number of trials
(iii) The probability of success must be the same for all the trials.
When coin is tossed, possible outcomes are Head and Tail.
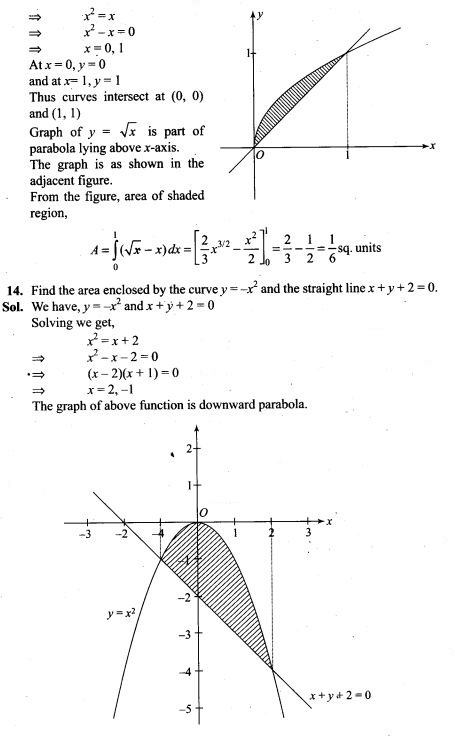
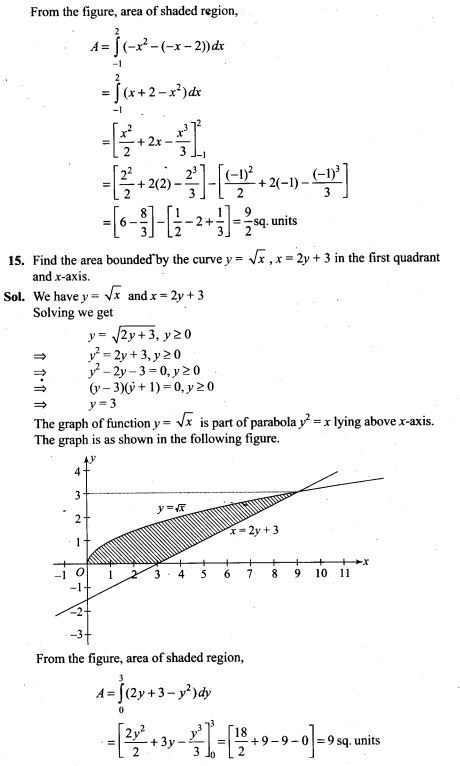
Since coin is tossed three times, we have fixed number of trials.
Also probability of Head and Tail in each trial is 1/2.
Thus given experiment is said to have binomial distribution.





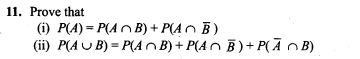
12. If X is the number of tails in three tosses of a coin, determine the standard deviation of X.


13. In a dice game, a player pays a stake of Rs 1 for each throw of a die. She receives Rs 5 if the die shows a 3, Rs 2 if the die shows a 1 or 6, and nothing otherwise. What is the player’s expected profit per throw over a long series of throws?

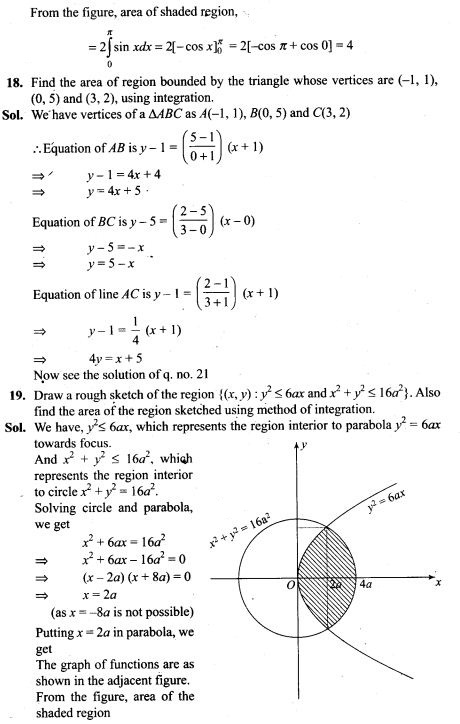
14. Three dice are thrown at the same time. Find the probability of getting three two’s, if it is known that the sum of the numbers on the dice was six.


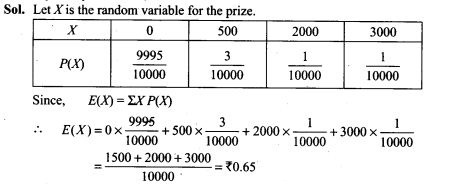
15. Suppose 10,000 tickets are sold in a lottery each for Rs 1. First prize is of Rs 3000 and the second prize is of Rs 2000. There are three third prizes of Rs.500 each. If you buy one ticket, what is your expectation?

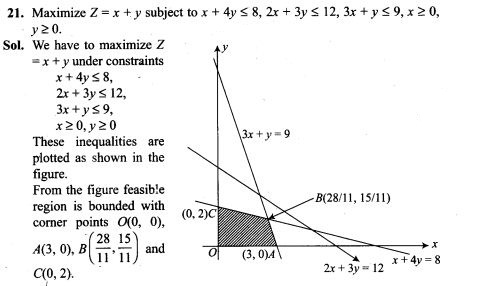
16. A bag contains 4 white and 5 black balls. Another bag contains 9 white and 7 black balls. A ball is transferred from the first bag to the second and then a ball is drawn at random from the second bag. Find the probability that the ball drawn is white.

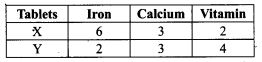
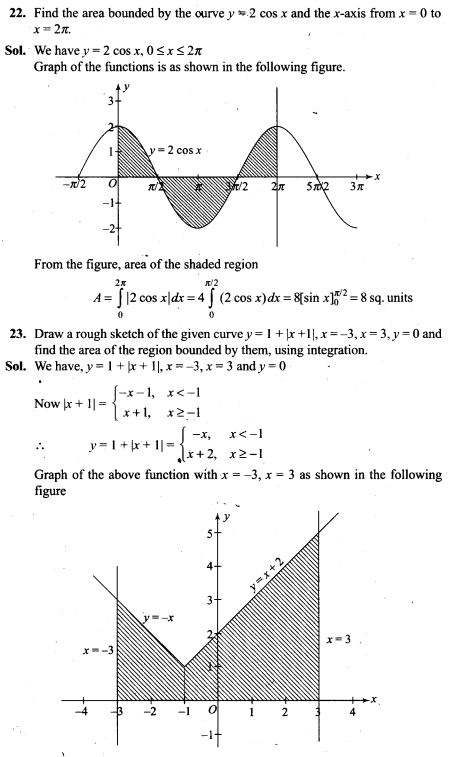
17. Bag I contains 3 black and 2 white balls, Bag II contains 2 black and 4 white balls. A bag and a ball is selected at random. Determine the probability of selecting a black ball.


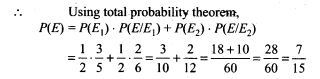
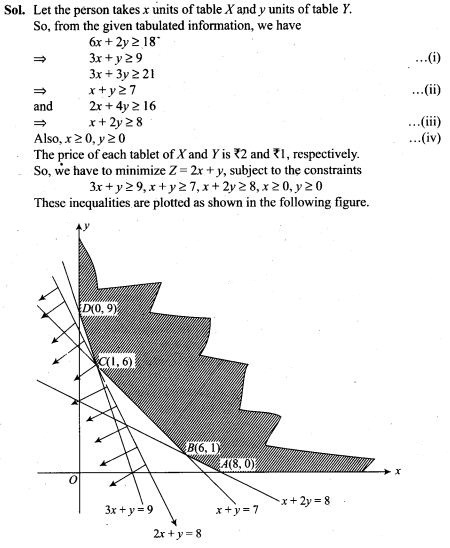
18. A box has 5 blue and 4 red balls. One ball is drawn at random and not replaced. Its colour is also not noted. Then another ball is drawn at random. What is the probability of second ball being blue?

19. Four cards are successively drawn without replacement from a deck of 52 playing cards. What is the probability that all the four cards are kings?

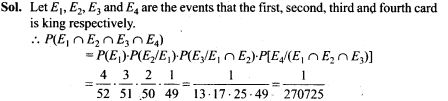
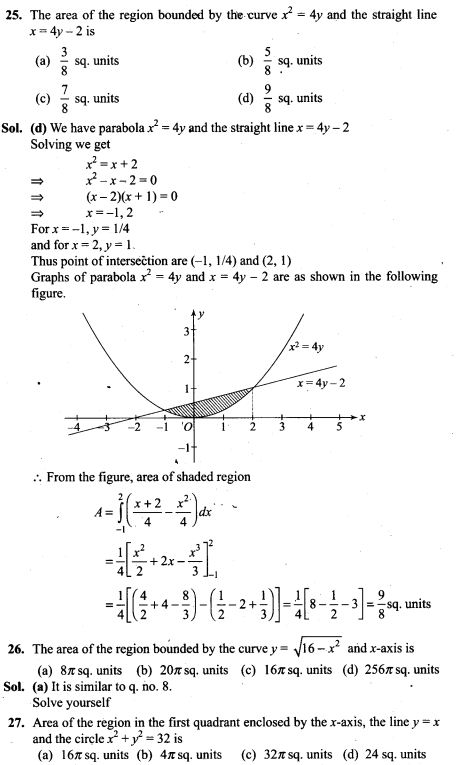
20. A die is thrown 5 times. Find the probability that an odd number will come up exactly three times.

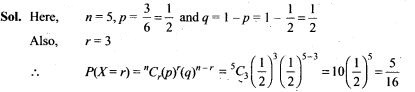
21. Ten coins are tossed. What is the probability of getting at least 8 heads?

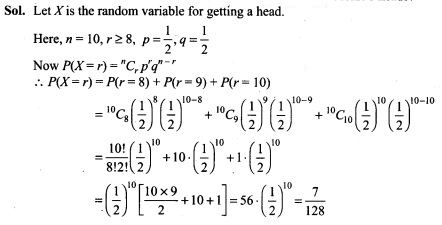
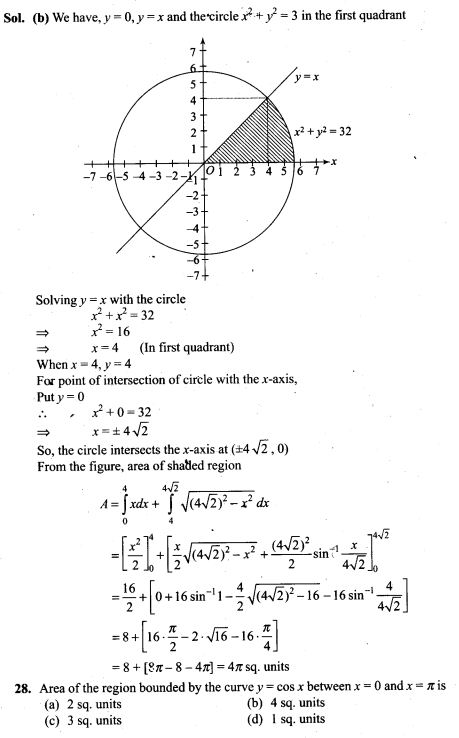
22. The probability of a man hitting a target is 0.25. He shoots 7 times. What is the probability of his hitting at least twice?

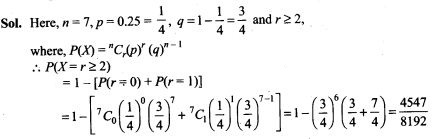
23. A lot of 100 watches is known to have 10 defective watches. If 8 watches are selected (one by one with replacement) at random, what is the probability that there will be at least one defective watch?






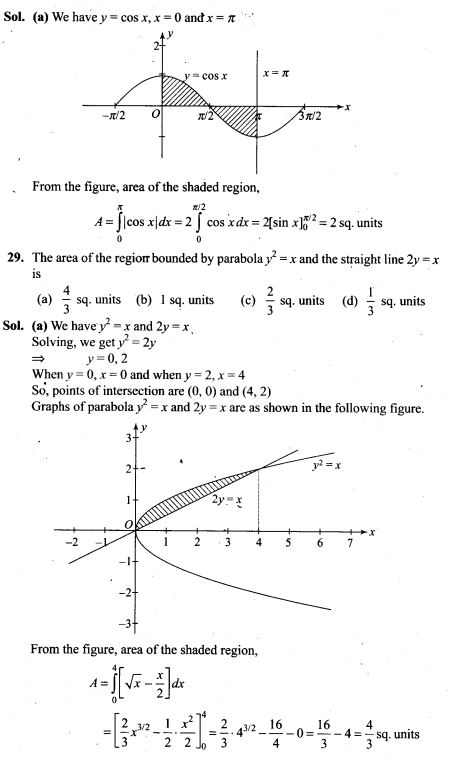
31. A factory produces bulbs. The probability that any one bulb is defective is 1/50 and they are packed in boxes of 10. From a single box, find the probability that
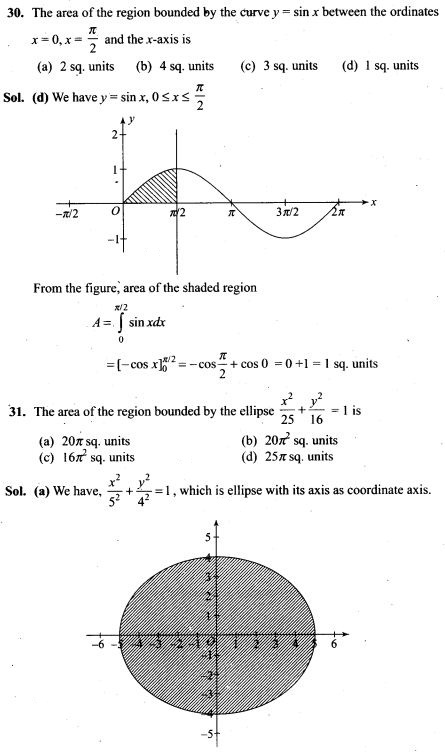
(i) none of the bulbs is defective
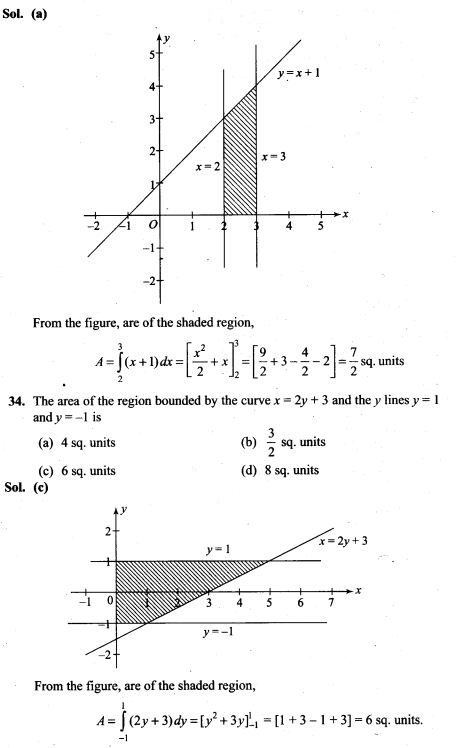
(ii) exactly two bulbs are defective
(iii) more than 8 bulbs work properly

32. Suppose you have two coins which appear identical in your pocket. You know that one is fair and one is 2-headed. If you take one out, toss it and get a head, what is the probability that it was a fair coin?

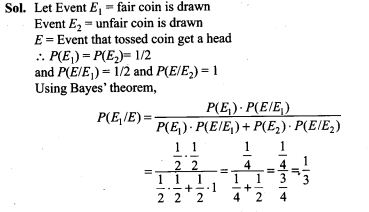
33. Suppose that 6% of the people with blood group O are left handed and 10% of those with other blood groups are left handed. 30% of the people have blood group O. If a left handed person is selected at . random, what is the probability that he/she will have blood group O?

35. Find the probability distribution of the maximum of the two scores obtained when a die is thrown twice . Determine also the mean of the distribution.




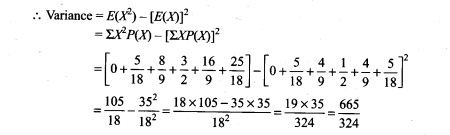
38. A and B throw a pair of dice alternately. A wins the game if he gets a total of 6 and B wins if she gets a total of 7. If A starts the game, find the probability of winning the game by A in third throw of the pair of dice.


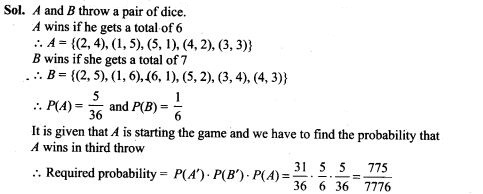
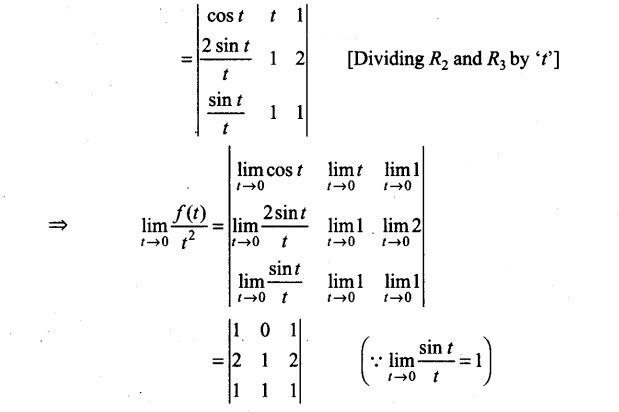
40. An um contains m white and n black balls. A ball is drawn at random and is put back into the um along with k additional balls of the same colour as that of the ball drawn. A ball is again drawn at random. Show that the probability of drawing a white ball now does not depend on k.

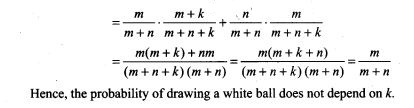
Long Answer Type Questions


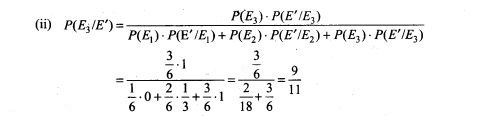
43. A shopkeeper sells three types of flower seeds A₁,A₂ and A₃. They are sold as a mixture where the proportions are 4:4:2 respectively. The germination rates of the three types of seeds are 45%, 60% and 35%. Calculate the probability
(i) of a randomly chosen seed to germinate
(ii) that it will not germinate given that the seed is of type A₃,
(iii) that it is of the type A₂ given that a randomly chosen seed does not germinate.

44. A letter is known to have come either from TATA NAGAR or from CALCUTTA. On the envelope, just two consecutive letter TA are visible. What is the probability that the letter came from TATA NAGAR.
Sol. Let Ex be the event that letter is from TATA NAGAR and E2 be the event that letter is from CALCUTTA.

45. There are two bags, one of which contains 3 black and 4 white balls while the other contains 4 black and 3 white balls. A die is thrown. If it shows up 1 or 3, a ball is taken from the 1st bag; but it shows up any other number, a ball is chosen from the second bag. Find the probability of choosing a black ball.

46. There are three urns containing 2 white and 3 black balls, 3 white and 2 black balls, and 4 white and 1 black balls, respectively. There is an equal probability of each urn being chosen. A ball is drawn at random from the chosen urn and it is found to be white. Find the probability that the ball drawn was from the second urn.


47. By examining the chest X ray, the probability that TB is detected when a person is actually suffering is 0.99. The probability of ah healthy person diagnosed to have TB is 0.001. In a certain city, 1 in 1000 people suffers from TB. A person is selected at random and is diagnosed to have TB. What is the probability that he actually has TB?

48. An item is manufactured by three machines A, B and C. Out of the total number of items manufactured during a specified period, 50% are manufactured on A, 30% on B and 20% on C. 2% of the items produced on A and 2% of items produced on B are defective, and 3% of these produced on C are defective. All the items are stored at one go down. One item is drawn at random and is found to be defective. What is the probability that it was manufactured on machine A?
Sol. Let E₁, E₂, E₃ be the event that item is manufactured on A,B and C respectively. Let E be the event that an item is defective.






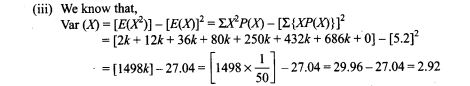
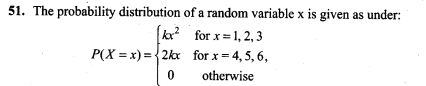
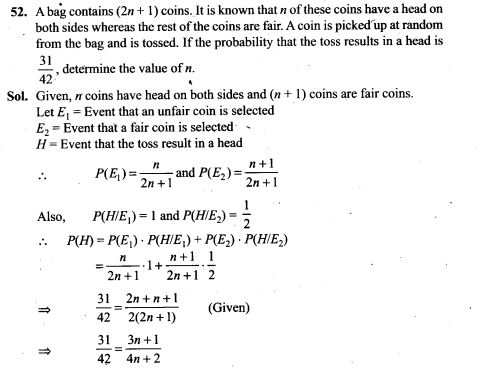
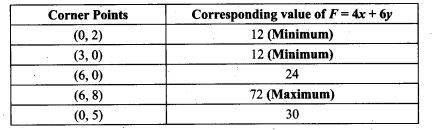
=> 124n + 62 = 126n + 42
=> 2n = 20=>n=10
53. Two cards are drawn successively without replacement from a well shuffled deck of cards. Find the mean and standard variation of the random variable X where X is the number of aces.

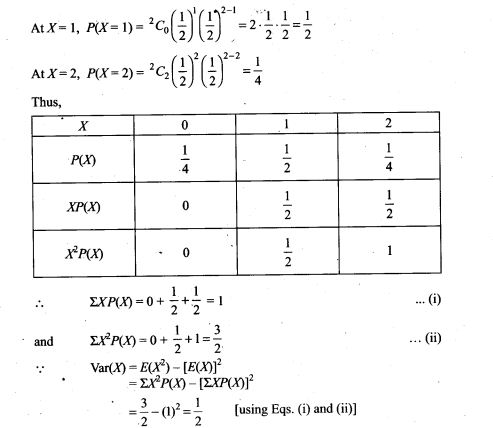
54. A die is tossed twice. A ‘success’ is getting an even number on a toss. Find the variance of the number of successes.


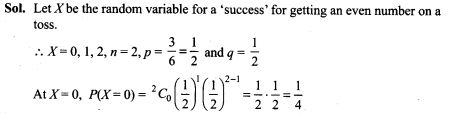
55. There are 5 cards numbered 1 to 5, one number on one card. Two cards are drawn at random without replacement. Let X denote the sum of the numbers on two cards drawn. Find the mean and variance of X.

Objective Type Questions





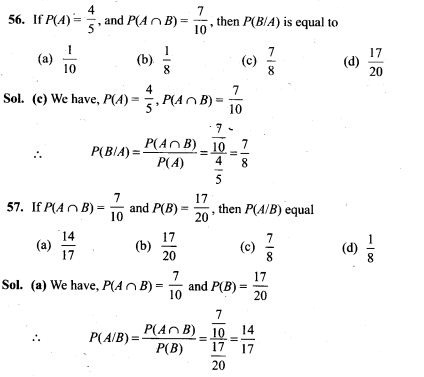
70. If two events are independent, then
(a) they must be mutually exclusive
(b) the sum of their probabilities must be equal to 1
(c) (A) and (B) both are correct
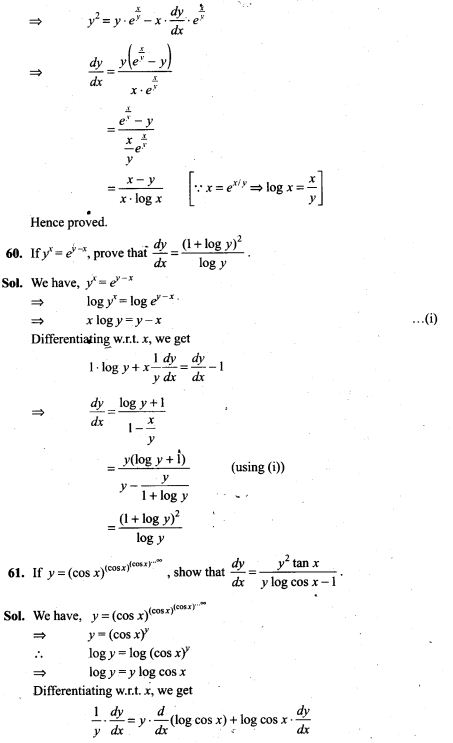
(d) None of the above is correct
Sol. (d) If two events A and B are independent, then we know that

If A and B are independent, knowledge that A occurred does not change the probabilities that B may have occurred. Whereas if A and B are disjoint, knowledge that A occurred completely changes the probabilities that B may have occurred by collapsing it to 0.




77. Assume that in a family, each child is equally likely to be a boy or a girl. A family with three children is chosen at random. The probability that the eldest child is a girl given that the family has at least one girl is

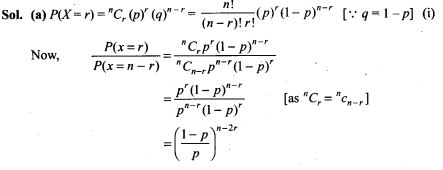
True/False Type Questions

Fill in the Blanks Type Questions

NCERT Exemplar Problems Class 12 Mathematics Chapter 12 Linear Programming

Short Answer Type Questions

4. Minimize Z = 13x- 15y subject to the constraints: x+y≤ 7,2x-3y + 6 ≥ 0, x ≥ 0, y ≥ 0.
Sol. We have to Minimize Z = 13x – 15y subject to the constraints x + y ≤7, 2x – 3y + 6 ≥ 0, x ≥ 0, y ≥ 0. These inequalities are plotted as shown in the following figure.

8. Refer to Exercise 7 above. Find the maximum value of Z.
Sol. Z is maximum at (3,2) and its maximum value is 47.

9. The feasible region for a LPP is shown in the following figure. Evaluate Z = 4x+y at each of the comer points of this region. Find the minimum value of Z, if it exists.

Now, we see that 3 is the smallest value of Z the comer point (0, 3). Note that here we see that, the region is unbounded, therefore 3 may not be the minimum value of Z. To decide this issue, we graph the inequality 4x + y < 3 and check whether the resulting open half plane has no point in common with feasible region otherwise, Z has no minimum value.
From the shown graph above, it is clear that there is no point in common with feasible region and hence Z has minimum value 3 at (0, 3).

10. In the following figure, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of Z = x + 2y

11. A manufacturer of electronic circuits has a stock of 200 resistors, 120 transistors and 150 capacitors and is required to produce two types of circuits A and B. Type A requires 20 resistors, 10 transistors and 10 capacitors. Type B requires 10 resistors, 20 transistors and 30 capacitors. If the profit on type A circuit is Rs 50 and that on type B circuit is Rs 60, formulate this problem as a LPP so that the manufacturer can maximise his profit.
Sol. Let the manufacture produces x units of type A circuits and y units of type B circuits. Form the given information, we have following corresponding constraint table.

12. A firm has to transport 1200 packages using large vans which can carry 200 packages each and small vans which can take 80 packages each. The cost for engaging each large van is Rs 400 and each small van is Rs 200. Not more than Rs 3000 is to be spent on the job and the number of large vans can not exceed the number of small vans. Formulate this problem as a LPP given that the objective is to minimise cost.
Sol. Let the firm has x number of large vans and y number of small vans.
From the given information, we have following corresponding constraint table.

13. A company manufactures two types of screws A and B. All the screws have to pass through a threading machine and a slotting machine. A box of Type A screws requires 2 minutes on the threading machine and 3 minutes on the slotting machine. A box of type B screws requires 8 minutes of threading on the threading machine and 2 minutes on the slotting machine. In a week, each machine is available for 60 hours. On selling these screws, the company gets a profit of Rs 100 per box on type A screws and Rs 170 per box on type B screws. Formulate this problem as a LPP given that the objective is to maximise profit.
Sol. Let the company manufactures x boxes of type A screws and y boxes of type B screws.
From the given information, we have following corresponding constraint table.

14. A company manufactures two types of sweaters: type A and type B. It costs Rs 360 to make a type A sweater and Rs 120 to make a type B sweater. The company can make at most 300 sweaters and spend at most Rs 72000 a day. The number of sweaters of type B cannot exceed the number of sweaters of type A by more than 100. The company makes a profit of Rs 200 for each sweater of type A and ?120 for every sweater of type B. Formulate this problem as a LPP to maximise the profit to the company.
Sol. Let the company manufactures x number of type A sweaters and y number of type B.
The company spend at most Rs 72000 a day.
∴ 360x + 120y ≤ 72000
=> 3x+y≤ 600 …(i)
Also, company can make at most 300 sweaters.
∴ x+y≤ 300 …(ii)
Also, the number of sweaters of type B cannot exceed the number of sweaters of type A by more than 100 i.e., y-x≤ 100
The company makes a profit of Rs 200 for each sweater of type A and Rs 120 for every sweater of type B
So, the objective function for maximum profit is Z = 200x + 120y subject to constraints.
3x+y≤ 600
x+y ≤ 300
x-y ≥ -100
x ≥ 0, y ≥ 0

15. A,man rides his motorcycle at the speed of 50 km/hour. He has to spend Rs 2 per km on petrol. If he rides it at a faster speed of 80 km/hour, the petrol cost increases to Rs 3 per km. He has atmost Rs120 to spend on petrol and one hour’s time. He wishes to find the maximum distance that he can travel. Express this problem as a linear programming problem.
Sol. Let the man rides to his motorcycle to a distance x km at the speed of 50 km/h and to a distance y km at the speed of 80 km/h.
Therefore, cost on petrol is 2x + 3y.
Since, he has to spend Rs120 atmost on petrol.
∴ 2x + 3y ≤ 120 …(i)
Also, he has at most one hour’s time.

Long Answer Type Questions
16. Refer to Exercise 11. How many of circuits of Type A and of Type B, should be produced by the manufacturer so as to maximize his profit? Determine the maximum profit.

22. A manufacturer produces two Models of bikes’-Model X and Model Y. Model X takes a 6 man-hours to make per unit, while Model Y takes 10 man-hours per unit. There is a total of 450 man-hour available per week. Handling and Marketing costs are Rs 2000 and Rs 1000 per unit for Models X and Y respectively. The total funds available for these purposes are Rs 80,000 per week. Profits per unit for Models X and Y are Rs 1000 and Rs 500, respectively. How many bikes of each model should the manufacturer produce so as to yield a maximum profit? Find the maximum profit.

So, for maximum profit manufacture must produces 25 number of models X and 30 number of model Y bikes.

23. In order to supplement daily diet, a person wishes to take some X and some Y tablets. The contents of iron, calcium and vitamins in X and Y (in milligrams per tablet) are given as below:

The person needs at least 18 milligrams of iron, 21 milligrams of calcium and 16 milligram of vitamins. The price of each tablet of X and Y is Rs 2 and Rs 1 respectively. How many tablets of each should the person take in order to satisfy the above requirement at the minimum cost?

From the figure, we can see the feasible region is unbounded region, with comer points as A(%, 0), B(6,1), C(I, 6), and D(0, 9)

Thus, the minimum value of Z is ‘8’ occurring at B( 1, 6). Since the feasible region is unbounded, ‘8’ may not be the minimum value of Z. To decide this, we plot the inequality 2x+y < 8 and check whether the resulting open half has points common with feasible region or not If it has common point, then 8 will not be the minimum value of Z, otherwise 8 will be the minimum value of Z. Thus, from the graph it is clear that, it has no common point.
Therefore, Z= 2x+y-has 8 as minimum value subject to the given constrains. Hence, the person should take 1 unit of X tablet and 6 units of Y tablets to satisfy the given requirements and at the minimum cost of Rs 8.

24. A company makes 3 models of calculators: A, B and C at factory I and factory II. The company has orders for at least 6400 calculators of model A, 4000 calculator of model B and 4800 calculator of model C. At factory I, 50 calculators of model A, 50 of model B and 30 of model C are made every day; at factory II, 40 calculators of model A, 20 of model B and 40 of model C are made everyday. It costs Rs 12000 and Rs 15000 each day to operate factory I and II, respectively. Find the number of days each factory should operate to minimize the operating costs and still meet the demand.

Objective Type Questions
26. The comer points of the feasible region determined by the system of linear constraints are (0,0), (0,40), (20,40), (60,20), (60,0). The objective function is Z=4x + 3y.
Compare the quantity in Column A and Column B
Column A Column B
Maximum of Z 325
(a) The quantity in column A is greater
(b) The quantity in column B is greater
(c) The two quantities are equal
(d) The relationship can not be determined on the basis of the information supplied .
Sol. (b)

28. Refer to Exercise 27. Maximum of Z occurs at
(a) (5,0) (b) (6,5) (c) (6, 8) (d) (4, 10)
Sol. (a) Refer to solution 27, maximum of Z occurs at (5, 0)
29. Refer to Exercise 27. (Maximum value of Z + Minimum value of Z) is equal to
(a) 13 (b) 1 (c) -13
Sol. (d) Refer to solution 27,
maximum value of Z + minimum value of Z = 15-32 = -17

31. Refer to Exercise 30. Minimum value of F is
(a) 0 (b) -16 . (c) 12 (d) does not exist
Sol. (b) Referring to solution 30, minimum value of F is -16 at (0,4).

32. Comer points of the feasible region for an LPP are (0, 2), (3, 0), (6,0), (6, 8) and (0,5).
Let F = 4x + 6y be the objective function.
The Minimum value of F occurs at
(a) (0,2) only
(b) (3,0) only
(c) the mid point of the line segment joining the points (0,2) and (3,0) only
(d) any point on the line segment joining the points (0,2) and (3, 0).
Sol. (d)

33. Refer to Exercise 32, Maximum of F – Minimum of F=
(a) 60 (b) 48 (c) 42 (d) 18
Sol. (a) Referring to the solution 32, maximum,of F-minimum of F= 72- 12 = 60

34. Comer points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px + qy, where p,q>0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1,1) is
(a) p = 2q (b )P=q\2 (c)p = 3q (d) p = q
Sol. (b)

Fill in the Blanks Type Questions
35. In a LPP, the linear inequalities or restrictions on the variables are called————-.
Sol. In a LPP, the linear inequalities or restrictions on the variables are called linear constraints.

36. In a LPP, the objective function is always————.
Sol. In a LPP, objective function is always linear.

37. If the feasible region for a LPP is————, then the optimal value of the objective function Z= axH-fiy may or may not exist.
Sol. If the feasible region for a LPP is unbounded, then the optimal value of the objective function Z = ax + by may or may not exist.

38. In a LPP if the objective function Z=ax+ by has the same maximum value on two comer points of the feasible region, then every point on the line segment joining these two points give the same————value.
Sol. In a LPP, if the objective function Z = ax + by has the same maximum value on two comer points of the feasible region, then every point on the line segment joining these two points gives the same maximum value.

39. A feasible region of a system of linear inequalities is said to be————if it can be enclosed within a circle.
Sol. A feasible region of a system of linear inequalities is said to be bounded, if it can be enclosed within a circle.

40. A comer point of a feasible region is a point in the region which is the———— of two boundary lines.
Sol. A comer point of a feasible region is a point in the region which is the intersection of two boundary lines.

41. The feasible region for an LPP is always a————polygon.
Sol. The feasible region for an LPP is always a convex polygon.

True/False Type Questions
42. If the feasible region for a LPP is unbounded, maximum or minimum of the objective function Z = ax+ by may or may not exist.
Sol. True

43. Maximum value of the objective function Z = ax+ by in a LPP always occurs
at only one comer point of the feasible region. ,
Sol. False

44. In a LPP, the minimum value of the objective function Z = ax+ by is always 0 if origin is one of the comer point of the feasible region.
Sol. False

45. In a LPP, the maximum value of the objective function Z = ax+ by is always finite.
Sol. True

NCERT Exemplar Problems Class 12 Mathematics Chapter 11 Three Dimensional Geometry

Short Answer Type Questions


5. Prove that the line through A(0, -1, -1) and B(4, 5, 1) intersects the line through C(3, 9,4) and D(- 4,4,4).
Sol. We know that, the equation of a line that passes through two points (x₁, y₁, z₁) and (x₂, y₂, z₂) is

7. Find the equation of a plane which bisects perpendicularly the line joining the points A(2, 3,4) and 5(4, 5, 8) at right angles.


8. Find the equation of a plane which is at a distance 3 √3 units from origin and the normal to which is equally inclined to coordinate axis.

9. If the line drawn from the point (-2, -1,-3) meets a plane at right angle at the point (1, -3, 3), find the equation of the plane.
Sol. Since, the line drawn from the point B(-2, -1,-3) meets a plane a plane at right angle at the point 4(1,-3, 3).
So, the plane passes through the point 4(1, -3, 3)

10. Find the equation of the plane through the points (2, 1, 0), (3, -2, -2) and (3, 1, 7).
Sol. We know that, the equation of a plane passing through three non-collinear points (x1. y1, z1), (x₂, y₂, z₂) and (x₃, y₃, z₃) is



14. O is the origin and A is (a, b, c). Find the direction cosines of the line OA and the equation of plane through A at right angle to OA.

Long Answer Type Questions



19. Find the equations of the line passing through the point (3,0,1) and parallel to the planes x + 2y = 0 and 3y-z = 0.


20. Find the equation of the plane through the points (2,1, -1) and (-1,3,4), and perpendicular to the plane x-2y + 4z = 10.


22. Find the equation of the plane which is perpendicular to the plane 5x + 3y + 6z + 8 = 0 and which contains the line of intersection of the planes x + 2y + 3z – 4 = 0 and 2x + y- z + 5 = 0.



27. Show that the straight lines whose direction cosines are given by 2l+2m -n=0 and mn + nl + lm = 0 are at right angles.

Objective Type Questions

30. If the directions cosines of a line are k, k, ‘k, then

33. The reflection of the point (α, β,γ) in the xy-plane is
(a) (α, β,0) (b) (0,0, γ) (c) (-α, -β, γ) (d) (α, β,-γ)
Sol. (d) In xy-plane, the reflection of the point (α, β,γ) is (α, β,-γ)
34. The area of the quadrilateral ABCD, where A(0,4,1), B(2, 3, -1), C(4, 5, 0) and D(2, 6,2) is equal to
(a) 9 sq. units (b) 18 sq. units (c) 27 sq. units (d) 81 sq. units

35. The locus represented by xy + yz = 0 is
(a) A pair of perpendicular lines (b) A pair of parallel lines
(c) A pair of parallel planes (d) A pair of perpendicular planes

Fill in the Blanks Type Questions

True/False Type Questions

NCERT Exemplar Problems Class 12 Mathematics Chapter 9 Differential Equations

Short Answer Type Questions

2. Find the differential equation of all non-vertical lines in a plane.

13. Form the differential equation having y = (sin^-1 x)²+ A cos^-1 x + B, where A and B are arbitrary constants, as its general solution.

14. Form the differential equation* of all circles which pass through origin and whose centres lie on y-axis.

19. Solve : (x + y)(dx -dy) = dx + dy
[Hint: Substitute x+y = z after separating dx and dy]

21. Solve the differential equation dy = cos x (2 – y cosec x) dx given that y=2 when x = π /2.

22. Form the differential equation by eliminating A and B in Ax² -By² = 1.

23. Solve the differential equation (1 +y²) tan^-1 x dx + 2y (1+x²)dy=0.

24. Find the differential equation of system of concentric circles with centre (1,2).

Long Answer Type Questions





31. Find the equation of a curve passing through origin if the slope of the tangent to the curve at any point (x, y) is equal to the square of the difference of the abscissa and ordinate of the point.

32. Find the equation of a curve passing through the point (1, 1). If the tangent drawn at any point P(x, y) on the curve meets the co-ordinate axes at A and B such that P is the mid-point of AB.

Objective Type Questions

60. Family y = Ax + A3 of curves will correspond to a differential equation of order ,
(a) 3 (b) 2 (c) 1 (d) not defined

62. The curve for which the slope of the tangent at any point is equal to the ratio of the abscissa to the ordinate of the point is
(a) an ellipse (b) parabola
(c) circle (d) rectangular hyperbola

Fill in the Blanks Type Questions

True/False Type Questions

NCERT Exemplar Problems Class 12 Mathematics Chapter 8 Applications of Integrals

Short Answer Type Questions

Long Answer Type Questions

Objective Type Questions

NCERT Exemplar Problems Class 12 Mathematics Chapter 7 Integrals

Short Answer Type Questions

Long Answer Type Questions

Objective Type Questions

Fill In the Blanks Type Questions

NCERT Exemplar Problems Class 12 Mathematics Chapter 6 Application of Derivatives

Short Answer Type Questions

Long Answer Type Questions

Objective Type Questions

Fill In the Blanks Type Questions
Fill in the blanks in each of the following exercises 60 to 64.

NCERT Exemplar Problems Class 12 Mathematics Chapter 5 Continuity and Differentiability

Short Answer Type Questions

Long Answer Type Questions

Objective Type Questions

Fill In the Blanks Type Questions

True/False Type Questions

NCERT Exemplar Problems Class 12 Mathematics Chapter 4 Determinants

Short Answer Type Questions
Direction for Exercises 1 to 6: Using the properties of determinants,

Long Answer Type Questions

Objective Type Questions

Fill In the Blanks Type Questions

True/False Type Questions