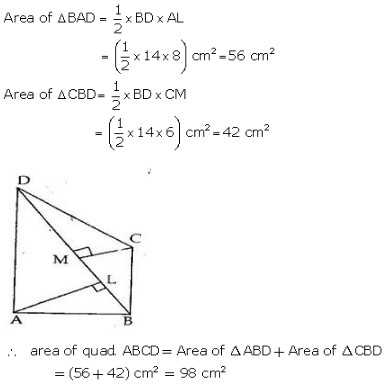
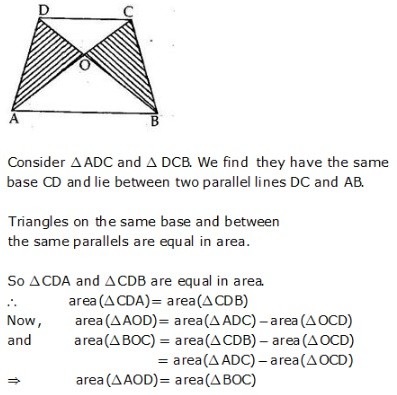
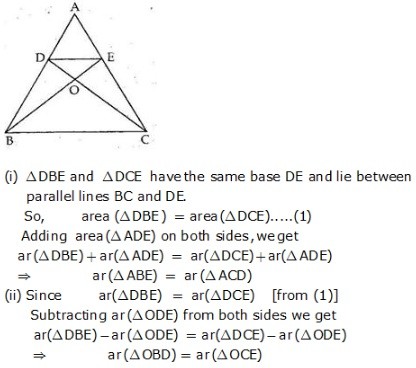
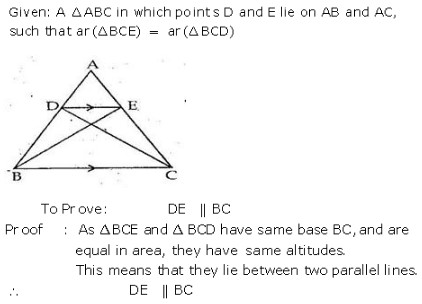
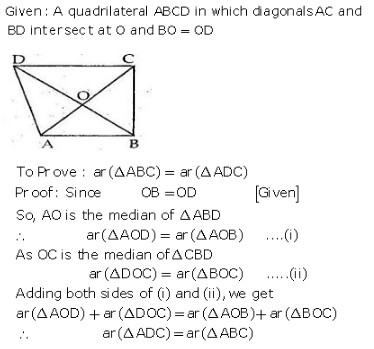
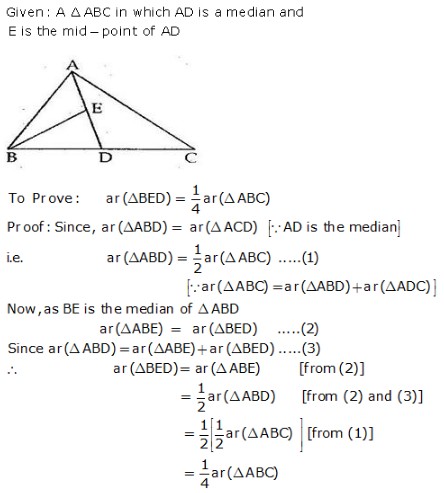
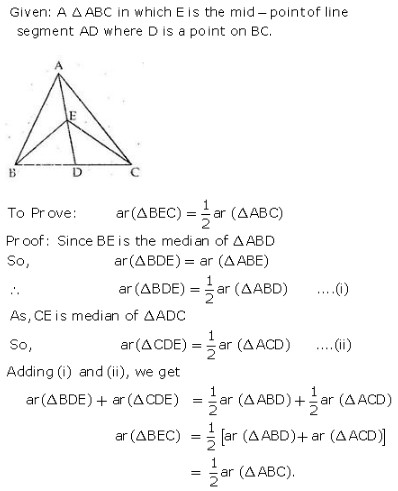
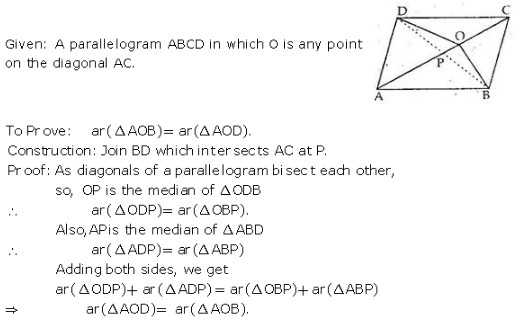
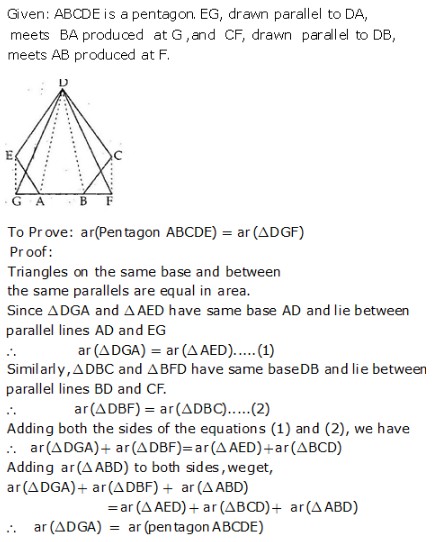
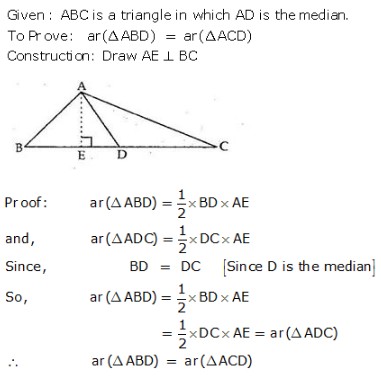
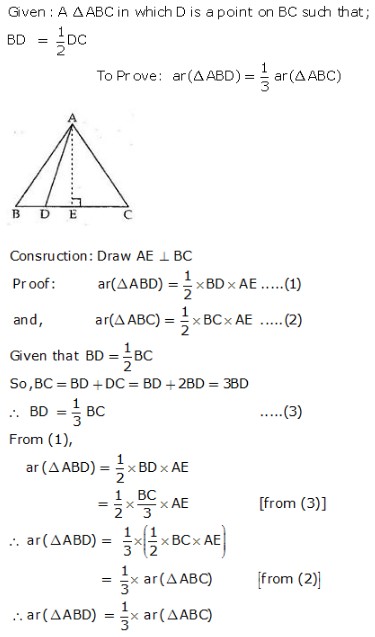
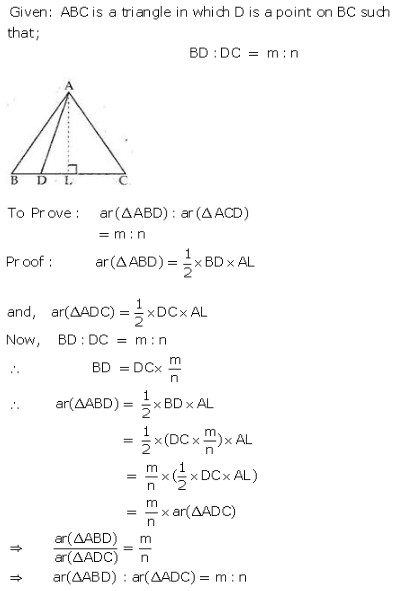
MEANING OF MONEY: Money is anything which is generally accepted as medium of exchange, measure of value, store of value and as means of standard of deferred payment. FUNCTIONS OF MONEY: Functions of money can be classified into Primary and Secondary
Primary/Basic functions:-
- Medium of Exchange: – It can be used in making payments for all transactions of
goods and services.
- Measure /Unit of value: – It helps in measuring the value of goods and services. The
value is usually called as price. After knowing the value of goods in single unit (price) exchanges become easy.
Secondary functions:-
- Standard of deferred payments: Deferred payments referred to those payments which
are to be made in near future.
Money acts as a standard deferred payment due to the following reasons:
- Value of money remains more or less constant compared to other commodities.
- Money has the merit of general acceptability.
- Money is more durable compare to other commodity.
- Store of value: Money can be stored and does not lose value
Money acts as a store of value due to the following reasons:
- It is easy and economical to store.
- Money has the merit of general acceptability.
- Value of money remains relatively constant
MONEY HAS OVERCOME THE DRAW BACKS OF BARTER SYSTEM:
- Medium of Exchange: Money has removed the major difficulty of the double coincidence of wants.
- Measure of value: Money has become measuring rod to measure the value of goods and services and is expressed in terms of price.
- Store of value: It is very convenient, easy and economical to store the value and has got general acceptability which was lacking in the barter system.
- Standard of deferred payments: Money has simplified the borrowing and lending of operations which were difficult under barter system. It also encourages capital formation.
MONEY SUPPLY: refers to total volume of money held by public at a particular point of time in an economy.
M1=currency held by public + Demand deposits + other deposits with Reserve Bank of India. M2=M1+saving deposits with post office saving bank M3=M1+net time deposit with the bank
M4=M3 + total deposits with post office saving bank excluding national saving certificate HIGH POWERED MONEY:
Refers to, currency with the public (notes +coins) and cash reserve of banks.
MONEY CREATION/DEPOSIT CREATION/CREDIT CREATION BY COMMERCIAL BANK
Let us understand the process of credit creation with the following example.
Suppose there is an initial deposit of Rs. 1000 and L.R.R. is 20% i.e., the banks have to keep Rs. 200 and lend Rs. 800/-. All the transactions are routed through banks. The borrower withdraws his Rs. 800/- for making payments which are routed through banks in the form of deposits account.
The Bank receives Rs. 800/- as deposit and keeps 20% of Rs.800/- i.e., Rs.160/- and lends Rs.640/- . Again the borrower uses this for payment which flows back into the banks thereby increasing the flow of deposits.
|
Deposits (in Rs.) |
Loans (in Rs.) |
Cash Reserve Ratio (20%) |
|
|
Initial deposit |
1000 |
800 |
200 |
|
First round |
800 |
640 |
160 |
|
Second round |
640 |
512 |
128 |
|
– |
– |
– |
– |
|
– |
– |
– |
– |
|
– |
– |
– |
– |
|
– |
– |
– |
– |
|
Total |
5000 |
4000 |
1000 |
MONEY MULTIPLIER:
Money Multiplier = 1/LRR. In the above example LRR is 20% i.e., 0.2, so money multiplier is equal to 1/0.2=5.
Why only a fraction of deposits is kept as Cash Reserve?
- All depositors do not withdraw the money at the same time.
- There is constant flow of new deposits into the banks.
MEANING: An apex body that controls, operates, regulates and directs the entire banking and monetary structure of the country.
- Currency authority or bank of issue: Central bank is a sole authority to issue currency in the country. Central Bank is obliged to back the currency with assets of equal value (usually gold coins, gold bullions, foreign securities etc.,)
Advantages of sole authority of note issue:
- Uniformity in note circulation
- Better supervision and control
- It is easy to control credit
- Ensures public faith
- Stabilization of internal and external value of currency
- Banker to the Government: As a banker it carries out all banking business of the Government and maintains current account for keeping cash balances of the government. Accepts receipts and makes payments for the government. It also gives loans and Advances to the government.
- Banker’s bank and supervisor: Acts as a banker to other banks in the country—
- Custodian of cash reserves:- Commercial banks must keep a certain proportion of cash reserves with the central bank (CRR)
- Lender of last resort: – When commercial banks fail to need their financial requirements from other sources, they approach Central Bank which gives loans and advances.
- Clearing house: – Since the Central Bank holds the cash reserves of commercial banks it is easier and more convenient to act as clearing house of commercial banks.
- Controller of money supply and credit: – Central Bank or RBI plays an important role during the times of economic fluctuations. It influences the money supply through quantitative and qualitative instruments. Former refers to the volume of credit and the latter refers to regulate the direction of credit.
- Custodian of foreign exchange reserves.
Another important function of Central Bank is the custodian of foreign exchange reserves. Central Bank acts as custodian of country’s stock of gold and foreign exchange reserves. It helps in stabilizing the external value of money and maintaining favorable balance of payments in the economy.
QUANTITATIVE INSTRUMENTS:
- Bank Rate policy: – It refers to the rate at which the central bank lends money to
commercial banks as a lender of the last resort.
Central Bank increases the bank rate during inflation (excess demand) and reduces the same in times of deflation (deficient demand)
- Open Market Operations: It refers to the buying and selling of securities by the
Central Bank from/ to the public and commercial banks.
It sells government securities during inflation/excess demand and buys the securities during deflation/deficient demand.
- Legal Reserve Ratio: R.B.I. can influence the credit creation power of commercial
banks by making changes in CRR and SLR
Cash Reserve Ratio (CRR): It refers to the minimum percentage of net demand and time liabilities to be kept by commercial banks with central bank.
Reserve Bank increases CRR during inflation and decreases the same during deflation
Statutory Liquidity Ratio (SLR): It refers to minimum percentage of net demand and time liabilities which commercial banks required to maintain with themselves. SLR is increased during inflation or excess demand and decreased during deflation or deficient demand.
- Margin Requirements: It is the difference between the amount of loan and market value of the security offered by the borrower against the loan.
Margin requirements are increased during inflation and decreased during deflation.
- Moral suasion: It is a combination of persuasion and pressure that Central Bank applies on other banks in order to get them act in a manner in line with its policy.
- Selective credit controls: Central Bank gives direction to other banks to give or not to give credit for certain purposes to particular sectors.
SHORT AND LONG ANSWER QUESTIONS
- Define Central Bank.
- Give the meaning of money.
- Discuss the functions of money.
- Describe how money over comes the problems of barter system?
- What are the measures of money supply?
- What do you mean by High powered money?
- Describe the process of money creation or credit creation by commercial banks.
- Why only a fraction of deposits is kept as Cash Reserves?
- Discuss the functions of Central Bank.
- Bring out the role of Central Bank as the controller of money supply or credit
- Explain the various qualitative and quantitative instruments used by the central bank in controlling the money supply during the times of a) excess demand/inflation b) deficient demand/deflation.
- Calculate the value money multiplier and the total deposit created if initial deposit is of Rs. 500 crores and LRR is 10%.
Ans: Money multiplier = 1/LRR which is equal to 1/0.1=10 Initial deposit Rs. 500 crores Total deposit = Initial deposit x money multiplier = 500 x 10 = 5000 crores.
Ans: Money multiplier = 1/LRR = 1/.25 = 4
Initial deposit = Total deposit / money multiplier = 12000/4 = 3000
- Calculate LRR, if initial deposit of Rs. 200 cores lead to creation of total deposits of Rs. 1600 cores.
Ans: Money multiplier = Total deposits/Initial deposits = 1600/200=8 Money multiplier = 1/LRR = 8=1/LRR.
LRR = 1.25 or 12.5
FREQUENTLY ASKED CBSE BOARD QUESTIONS
One Mark Questions (1M)
- Define money.
- Ml =
- What is meant by barter system?
- Write two drawbacks of barter exchange.
- List out two main functions of money.
- Define commercial bank.
- Give the meaning of central bank.
- What do you mean by credit creation by commercial banks.
- Define bank rate.
- Define cash reserve ratio.
- Give the meaning of statutory liquidity ratio.
- What is meant by open market operations (OMO)?
- Define money supply.
- Write one difference between commercial bank and central bank.
- Mention two important functions of central bank.
Three Marks Questions (3M)
- Explain briefly any two main functions of money.
- How does the central bank apply bank rate as a measure of credit control?
- What are the components of M1?
- State any THREE functions of central bank. Explain any one.
- Explain the “lender of last resort” function of central bank.
- What is money multiplier?
- Explain briefly any three drawbacks of barter system
- Explain the open market operations method of credit control used by a central bank. Four Marks Questions (4 M)
- Distinguish between commercial banks and central bank.
- Explain how money solves the drawbacks of barter exchange.
- What is money multiplier? How will you determine its value?
- Briefly explain any TWO quantitative measures of credit control by the central bank.
- Explain briefly the credit creation by commercial banks with the help of an example.


























































































 , find x and y
, find x and y





























 = x = 4/9
= x = 4/9 
 = x = 37/99
= x = 37/99 both are rational numbers
both are rational numbers

 Question 4:
Question 4: Question 5:
Question 5: Question 6:
Question 6: Question 7:
Question 7:
 Question 9:
Question 9: Question 10:
Question 10: Question 11:
Question 11:
 Question 13:
Question 13: Question 14:
Question 14:
 Question 16:
Question 16: Question 17:
Question 17: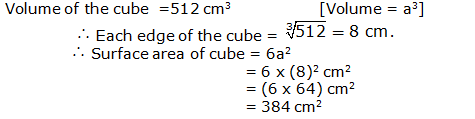 Question 18:
Question 18:
 Question 20:
Question 20: Question 1:
Question 1:
 Question 3:
Question 3: Question 4:
Question 4:
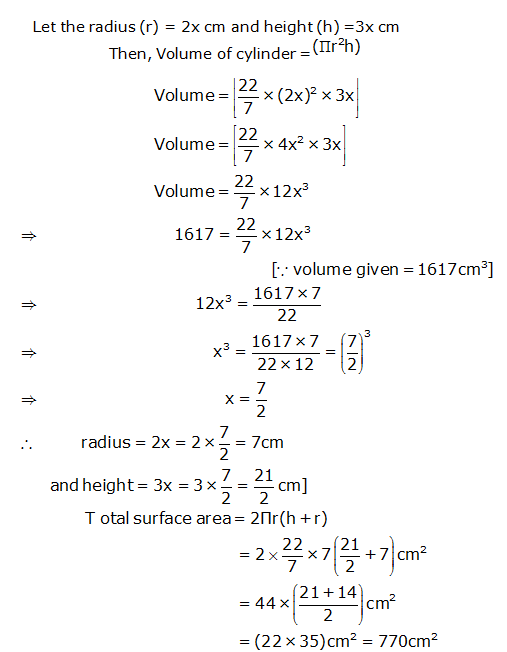 Question 6:
Question 6:
 Question 8:
Question 8:
 Question 10:
Question 10: Question 11:
Question 11:
 Question 13:
Question 13: Question 14:
Question 14: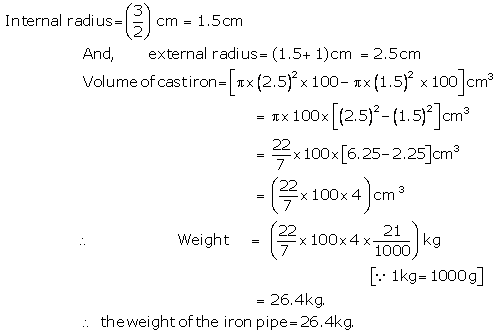 Question 15:
Question 15:
 Question 17:
Question 17: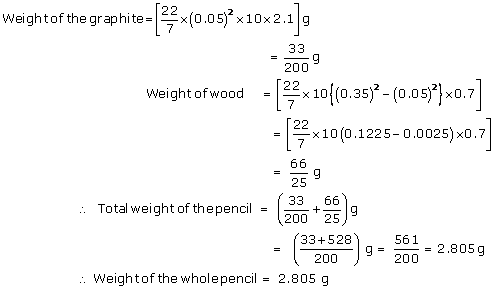 Question 18:
Question 18:
 Question 2:
Question 2: Question 3:
Question 3:
 Question 6:
Question 6: Question 7:
Question 7: Question 8:
Question 8: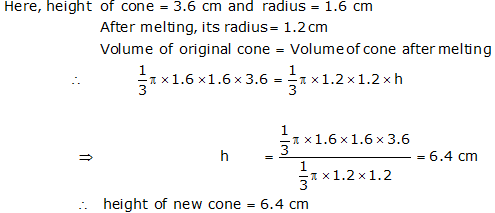
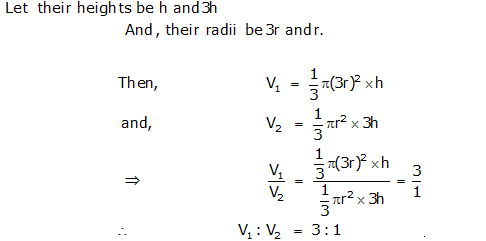 Question 10:
Question 10: Question 11:
Question 11: Question 12:
Question 12:
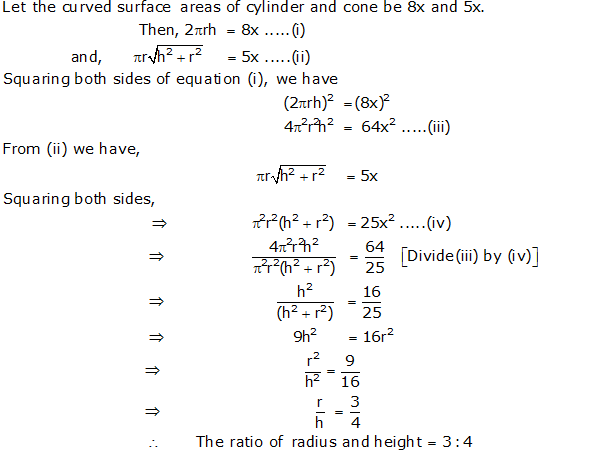 Question 14:
Question 14: Question 15:
Question 15:
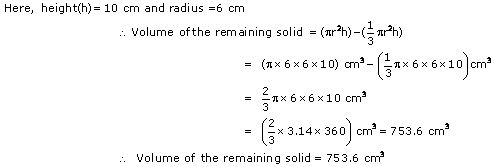 Question 17:
Question 17: Question 18:
Question 18: Question 1:
Question 1:
 Question 3:
Question 3: Question 4:
Question 4:
 Question 6:
Question 6: Question 7:
Question 7: Question 8:
Question 8: Question 9:
Question 9: Question 10:
Question 10:
 Question 12:
Question 12:
 Question 14:
Question 14: Question 15:
Question 15:
 Question 17:
Question 17: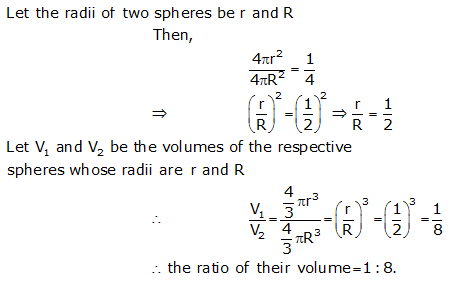 Question 18:
Question 18: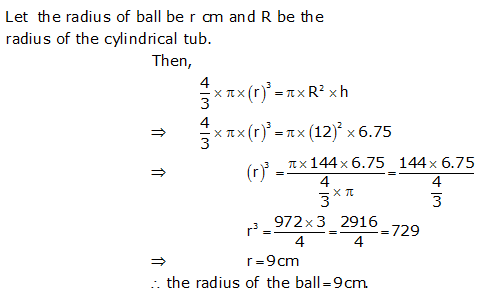
 Question 20:
Question 20: Question 21:
Question 21: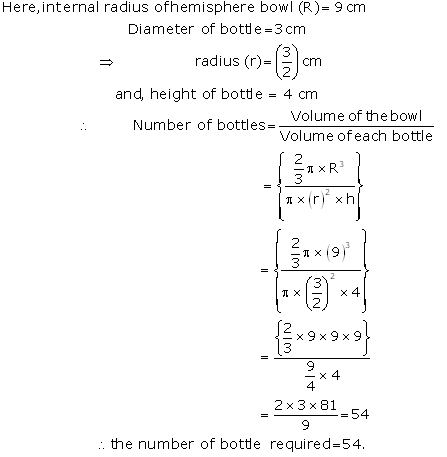
 Question 23:
Question 23:






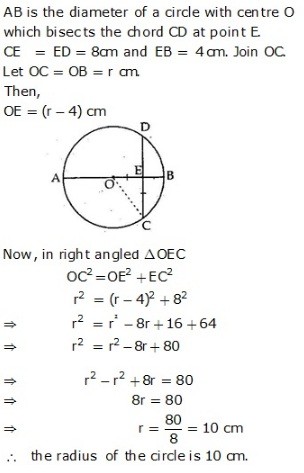


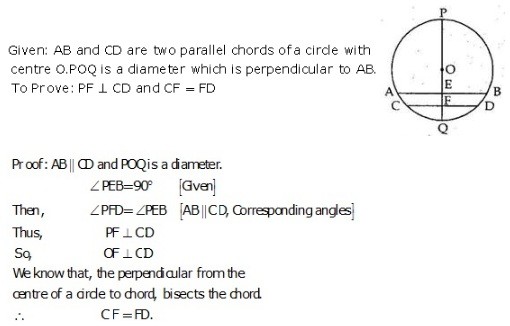



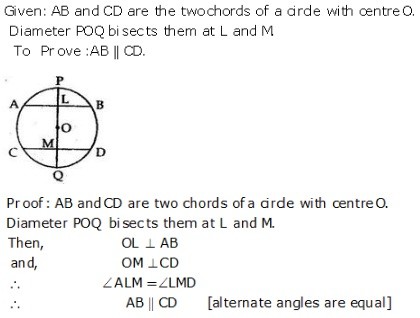




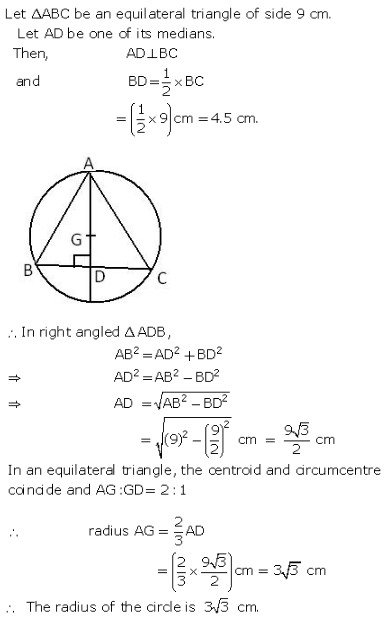


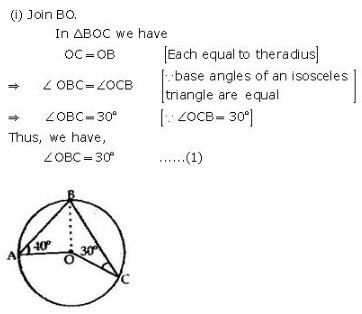
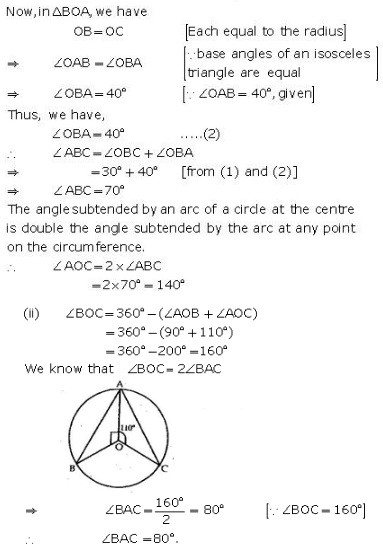


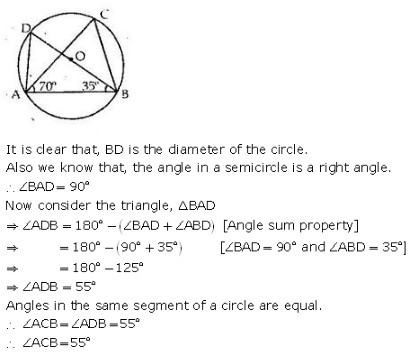
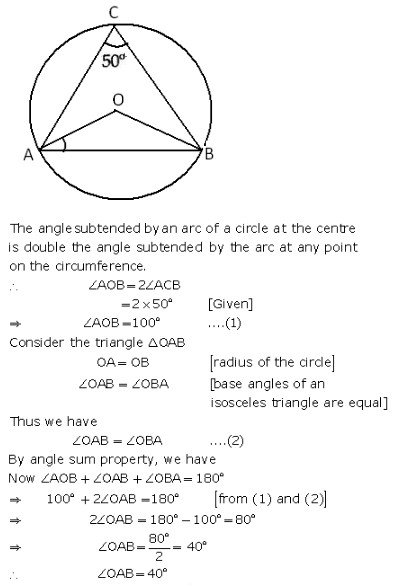






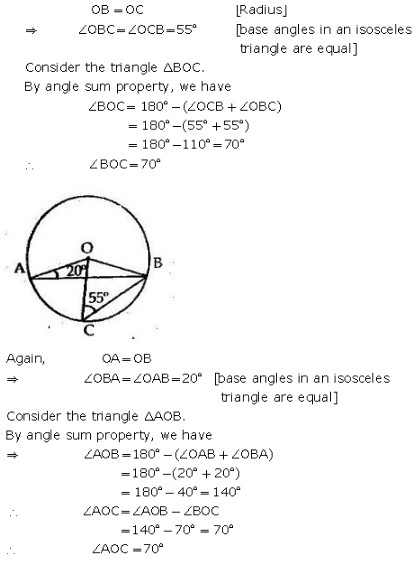



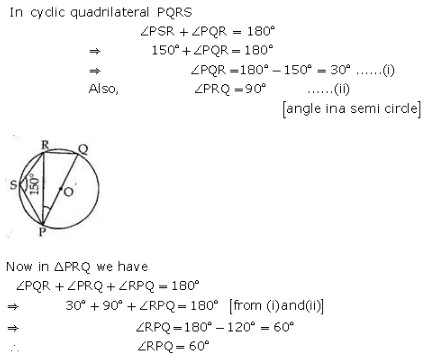


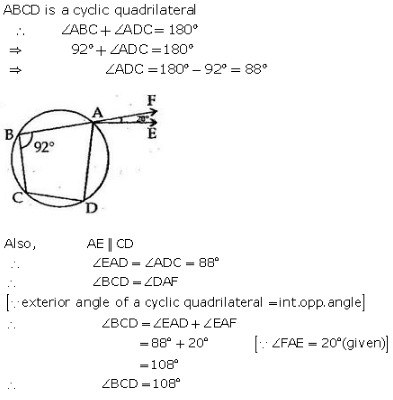







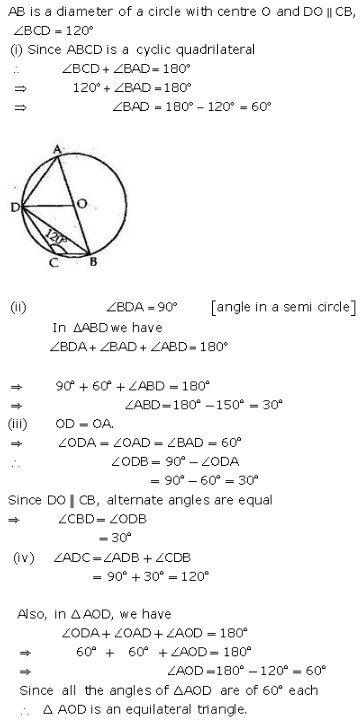



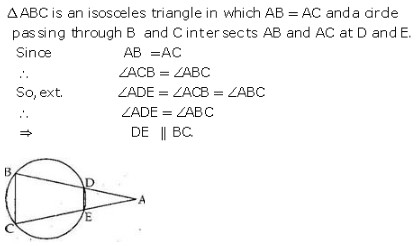
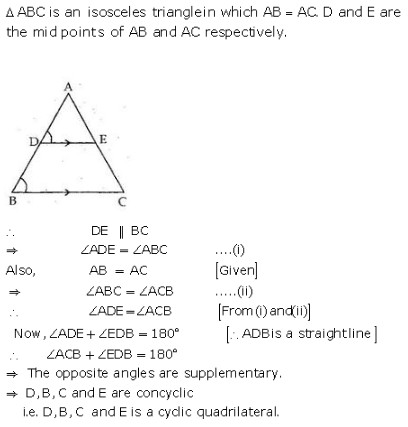

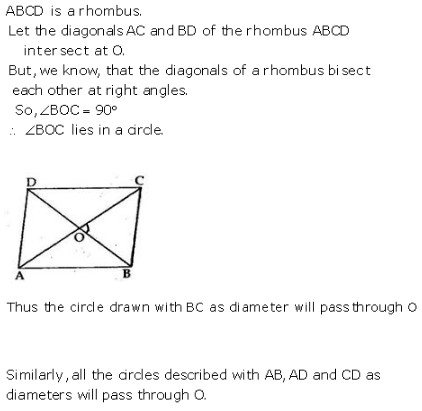



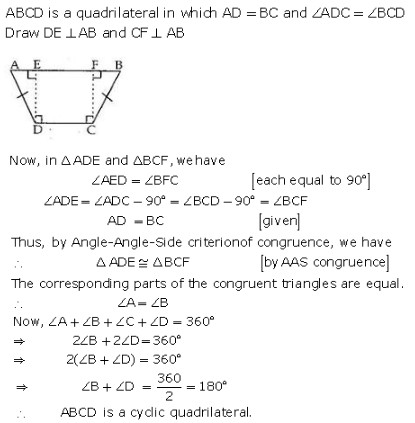





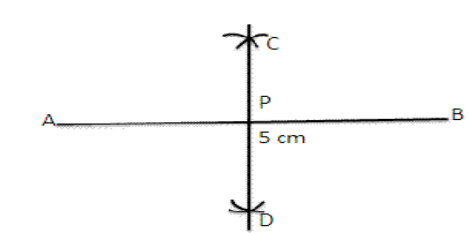
 Exercise 12A
Exercise 12A
 Question 5:
Question 5: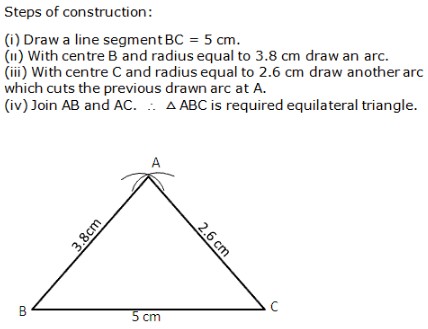 Question 6:
Question 6: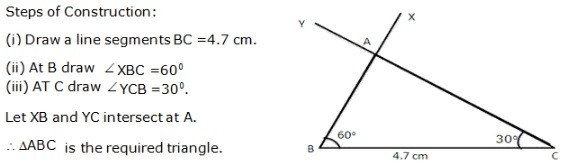
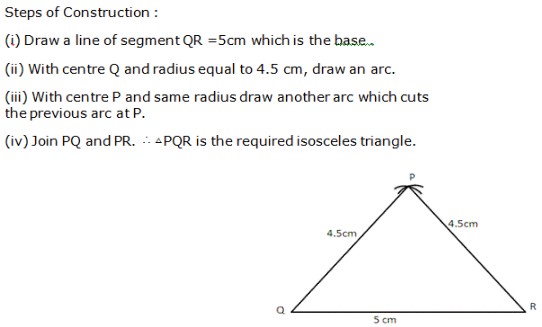 Question 8:
Question 8: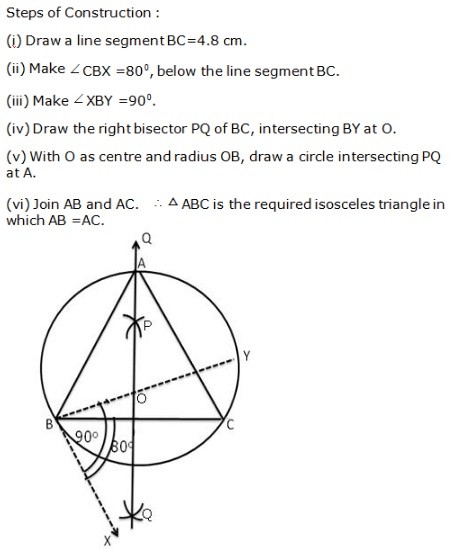 Question 9:
Question 9: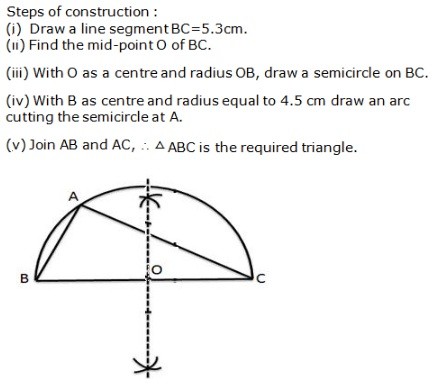
 Question 11:
Question 11:
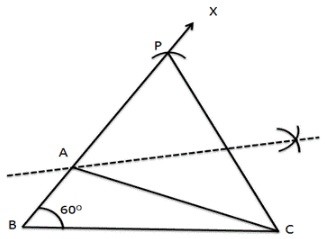
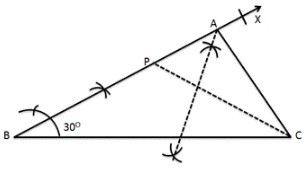



 Question 2:
Question 2: Question 3:
Question 3:
 Question 4:
Question 4: Question 5:
Question 5:
 Question 7:
Question 7: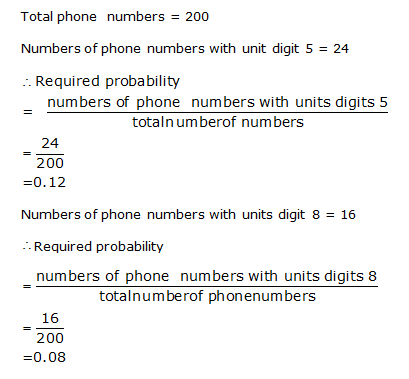 Question 8:
Question 8: Question 9:
Question 9: