Ultimate Blogging Championship

Category: Classes

  • Chapter 15 Probability Notes for Class 9th Maths


    Chapter 1 5 Probability

    • Probability: Probability is a quantitative measure of certainty.
    • Experiment: A job which produces some outcomes.
    • Trial: Performing an experiment.
    • Event: The group of outcomes, denoted by capital letter of English alphabets like A, B, E etc.
    • The empirical (or experimental) probability P(E) of an event E is given by

    • The probability of an event lies between 0 and 1 (0 and 1 are included)
    • Impossible event: Event which never happen.
    • Certain event: Event which definitely happen.
    • The probability of sure event is 1.
    • The probability of an impossible event is 0.
    • The probability of an event E is a number P(E) such that 0 < P(E) < I.

  • Chapter 14 Statistics Notes for Class 9th Maths

    1. Collection of Data
    2. Presentation of Data
    3. Graphical Representation of Data
    4. Measures of Central Tendency

  • Chapter 13 Surface Areas and Volumes Notes for Class 9th Maths


    Chapter 13 Surface Areas and Volumes

    1. Surface Area of a Cuboid and a Cube
    2. Surface Area of a Right Circular Cylinder
    3. Surface Area of a Right Circular Cone
    4. Surface Area of a Sphere
    5. Volume of a Cuboid
    6. Volume of a Cylinder
    7. Volume of a Right Circular Cone
    8. Volume of a Sphere


  • Chapter 12 Heron’s Formula Notes for Class 9th Maths


    Chapter 12 Heron’s Formula

    1. Area of a Triangle – by Heron’s Formula
    2. Application of Heron’s Formula in finding Areas of Quadrilaterals
    • Triangle with base ‘b’ and altitude ‘h’ is


  • Chapter 11 Constructions Notes for Class 9th Maths

    Chapter 11 Constructions

    • Basic Constructions
    • Some Constructions of Triangles
    1. Use only ruler and compass while drawing constructions.
    2. Protractor may be used for drawing non-standard angles.
    3. Constructions of a triangle given its base, a base angle and the difference of the other two sides.
    4. Constructions of a triangle given its perimeter and its two base angles.
    5. A triangle can be constructed if its perimeter and two base angles are given.
    6. Geometrical construction is the process of drawing a geometrical figure using only two instruments-an ungraduated ruler and a pair of compasses.
    7. Some specific angles like 15°,30o,45o,60o,75o,90°, etc. can be constructed without using protractor.
    8. A triangle can be constructed if its base, base angle and the sum of the two sides or the difference of the other two sides are given.

  • Chapter 10 Circles Notes for Class 9th Maths


    Chapter 10 Circles

    • Circles and its Related Terms : A Review
    • Angle Subtended by a Chord at a Point
    • Perpendicular from the Centre to a Chord
    • Circle through Three Points
    • Equal Chords and their Distances from the Centre
    • Angle Subtended by an Arc of a Circle
    • Cyclic Quadrilaterals
    • Circle- circle is locus of such points which are at equidistant from a fixed point in a plane.
    • Concentric circle- Circle having same centre called concentric circle.
    • Two arc of a circle called congruent if they have the same degree measure.
    • If two arc equal then their corresponding chords are equal.
    • The perpendicular from centre to chord of circle, it bisects the chord and converse.
    • There is one and only one circle passing through three non-collinear points.
    • Equal chords of circle are equidistant from centre.
    • The angle subtend by an arc at the centre of circle is twice the angle which subtend at remaining part of circumference.
    • Any two angles in the same segment of the circle are equal.
    • Angle of semicircle is right angle.
    • Equal chords of circle subtend equals angle at the centre of circle.
    • If the all vertices of a quadrilateral lie on the circumference of circle, then quadrilateral called cyclic.
    • In a cycle quadrilateral the sum of opposite angles is 180o and converse.
    • The exterior angle of a cycle quadrilateral is equal to the opposite interior angle.

  • Chapter 9 Areas of Parallelograms and Triangles Notes for Class 9th Maths


    Chapter 9 Areas of Parallelograms and Triangles

    1. Figures on the same Base and Between the same Parallels
    2. Parallelograms on the same Base and between the same Parallels
    3. Triangles on the same Base and between the same Parallels





    • If a parallelogram and a triangle are on the same base and between the same parallel, then

    area of the triangle is equal to one half area of the parallelogram.

    • A median AD of a AABC divides it into two triangles of equal areas. Therefore ar(AABD)=ar(ACD )
    • If the medians of a intersect at G, then ar(AAGB)=ar(AAGC )=ar(ABGC )=1 ar (AABC)

    • Triangles with equal bases and equal areas have equal corresponding altitude.

  • Chapter 8 Quadrilaterals Notes for Class 9th Maths

    Chapter 8 Quadrilaterals

    • Angle Sum Property of a Quadrilateral
    • Types of Quadrilaterals
    • Properties of a Parallelogram
    • The Mid-Point Theorem
    1. Sum of the angles of a quadrilateral is 360o
    2. A diagonals of a parallelogram divides it into two congruent triangles.
    3. In a parallelogram
    4. diagonals bisect each other.
    5. opposite angles are equal.
    6. opposite sides are equal
    7. Diagonals of a square bisects each other at right angles and are equal, and vice-versa.
    8. A line through the mid-point of a side of a triangle parallel to another side bisects the third side. (mid-point theorem)
    9. The line through the mid points of sides of a D || to third side and half of it.
    10. A quadrilateral is a parallelogram, if
    11. its opposite angles are equal.
    12. its opposite sides are equal.
    13. its diagonals bisect each other.
    14. a pair of opposite sides is equal and parallel.
    15. Diagonals of a rectangle bisect each other and are equal and vice-versa.
    16. Diagonals of a rhombus bisect each other at right angles and vice-versa.
    17. A line through the mid-point of a side of a triangle parallel to another side bisects the third side.
    18. The line-segment joining the mid-points of any two sides of a triangle is parallel to the third side and is half of it.

  • Chapter 7 Triangles Notes for Class 9th Maths


    Chapter – 7 Triangles

    1. Congruence of Triangles
    2. Criteria for Congruence of Triangles
    3. Some Properties of a Triangle
    4. Inequalities in a Triangle
    • Triangle- A closed figure formed by three intersecting lines is called a triangle. A triangle has three sides, three angles and three vertices.
    • Congruent figures- Congruent means equal in all respects or figures whose shapes and sizes are both the same for example, two circles of the same radii are congruent. Also two squares of the same sides are congruent.
    • Congruent Triangles- two triangles are congruent if and only if one of them can be made to superpose on the other, so as to cover it exactly.

    • If two triangles ABC and PQR are congruent under the correspondence A « P, B « Q and C « R then symbolically, it is expressed as DABC @ DPQR

    • In congruent triangles corresponding parts are equal and we write ‘CPCT’ for corresponding parts of congruent triangles.

    • SAS congruency rule – Two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle. For example: DABC and DPQR as shown in the figure satisfy SAS congruent criterion.


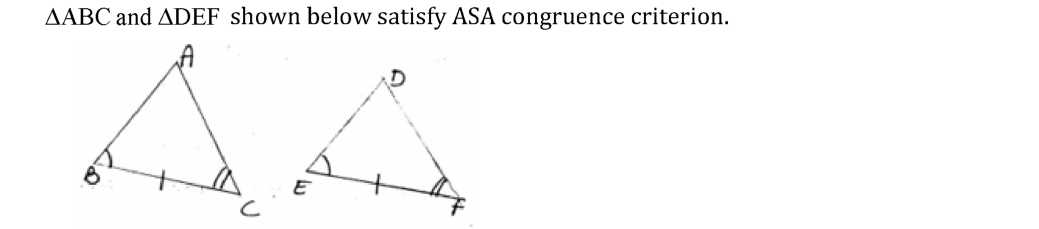
    • ASA Congruence Rule- Two triangles are congruent if two angles and the included side of

    one triangle are equal to two angles and the included side of other triangle. For examples

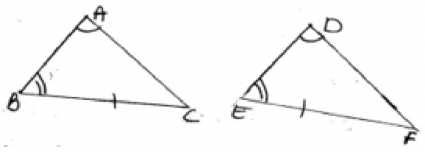
    • AAS Congruence Rule- Two triangle are congruent if any two pairs of angles and one pair of corresponding sides are equal for example DABC and DDEF shown below satisfy AAS
    • Angle opposite to equal sides of a triangle are equal.

    congruence criterion.

    • AAS criterion for congruence of triangles is a particular case of ASA criterion.
    • Isosceles Triangle- A triangle in which two sides are equal is called an isosceles triangle.

    • Sides opposite to equal angles of a triangle are equal.
    • Each angle of an equilateral triangle is 60o.
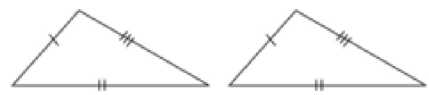
    • SSS congruence Rule – If three sides of one triangle are equal to the three sides of another triangle then the two triangles are congruent for example DABC and DDEF as shown in

    the figure satisfy SSS congruence criterion.

    • RHS Congruence Rule- If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle then the two triangle are congruent. For example: DABCand DPQR shown below satisfy RHS

    congruence criterion.


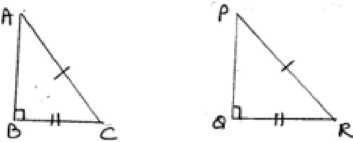
    RHS stands for right angle – Hypotenuse side.

    • A point equidistant from two given points lies on the perpendicular bisector of the line segment joining the two points and its converse.
    • A point equidistant from two intersecting lines lies on the bisectors of the angles formed by the two lines.
    • In a triangle, angle opposite to the longer side is larger (greater)
    • In a triangle, side opposite to the large (greater) angle is longer.
    • Sum of any two sides of a triangle is greater than the third side.

  • Chapter 6 Lines and Angles Notes for Class 9th Maths

    Chapter – 6 Lines and Angles

    1. Basic Terms and Definitions
    2. Intersecting Lines and Non-Intersecting Lines
    3. Pairs of Angles
    4. Parallel Lines and a Transversal
    5. Lines Parallel to the same Line
    6. Angle Sum Property of a Triangle
    7. Point- We often represent a point by a fine dot made with a fine sharpened pencil on a piece of paper.
    8. Line- A line is completely known if we are given any two distinct points. Line AB is represented by as AB . A line or a straight line extends indefinitely in both the directions.

    (5) Collinear points- If three or more points lie on the same line, they are called collinear points otherwise they are called non-collinear points.

    Types of Angles-

    1. Acute angle- An acute angle measure between Oo and 90o
    2. Right angle- A right angle is exactly equal to 90o
    3. Obtuse angle- An angle greater than 90o but less than 180o
    4. Straight angle- A straight angle is equal to 180o
    5. Reflex angle- An angle which is greater than 180o but less than 360o is called a reflex angle.
    6. Complementary angles- Two angles whose sum is 90o are called complementary angles.
    7. Supplementary angle- Two angles whose sum is 180o are called supplementary angles.
    8. Adjacent angles- Two angles are adjacent, if they have a common vertex, a common arm and their non-common arms are on different sides of common arm.
    9. Linear pair- Two angles form a linear pair, if their non-common arms form a line.
    10. Vertically opposite angles- Vertically opposite angles are formed when two lines intersect each other at a point.

    TRANSVERSAL:

    1. Corresponding angles
    2. Alternate interior angles
    3. Alternate exterior angles
    4. Interior angles on the same side of the transversal.
    • If a transversal intersects two parallel lines, then
    1. each pair of corresponding angles is equal.
    2. each pair of alternate interior angles is equal.
    3. each pair of interior angle on the same side of the transversal is supplementary.
    • If a transversal interacts two lines such that, either
    1. any one pair of corresponding angles is equal, or
    2. any one pair of alternate interior angles is equal or

    (iii) any one pair of interior angles on the same side of the transversal is supplementary then the lines are parallel.

    • Lines which are parallel to a given line are parallel to each other.
    • The sum of the three angles of a triangle is 180°
    • If a side of a triangle is produced, the exterior angle so formed is equal to the sum of the two interior opposite angles.