Angles, Linesand Triangles
Question 1:
Exercise 4A
-
Angle: Two rays having a common end point form an angle.
-
Interior of an angle: The interior of ∠AOB is the set of all points in its plane, which lie on the same side of OA as B and also on same side of OB as A.
-
Obtuse angle: An angle whose measure is more than 90° but less than 180°, is called an obtuse angle.
-
Reflex angle: An angle whose measure is more than 180° but less than 360° is called a reflex angle.
-
Complementary angles: Two angles are said to be complementary, if the sum of their measures is 90o.
-
Supplementary angles: Two angles are said to be supplementary, if the sum of their measures is 180°.
Question 2:
∠A = 36° 27′ 46″ and ∠B = 28° 43′ 39″
∴ Their sum = (36° 27′ 46″) + (28° 43′ 39″)

Therefore, the sum ∠A + ∠B = 65° 11′ 25″
Question 3:
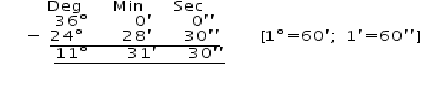
Let ∠A = 36° and ∠B = 24° 28′ 30″ Their difference = 36° – 24° 28′ 30″
Thus the difference between two angles is ∠A – ∠B = 11° 31′ 30″
Question 4:
-
-
Complement of 58o = 90o – 58o = 32o
-
Complement of 16o = 90 – 16o = 74o
-
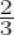
of a right angle =
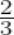
× 90o = 60o Complement of 60o = 90o – 60o = 30o
-
1o = 60′
⇒ 90o = 89o 60′
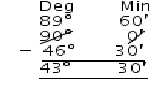
Complement of 46o 30′ = 90o – 46o 30′ = 43o 30′ (v) 90o = 89o 59′ 60″
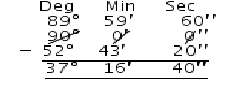
Complement of 52o 43′ 20″ = 90o – 52o 43′ 20″
= 37o 16′ 40″
(vi) 90o = 89o 59′ 60″

∴ Complement of (68o 35′ 45″)
= 90o – (68o 35′ 45″)
= 89o 59′ 60″ – (68o 35′ 45″)
= 21o 24′ 15″
Question 5:
-
Supplement of 63o = 180o – 63o = 117o
-
Supplement of 138o = 180o – 138o = 42o
-
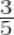
of a right angle =
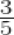
× 90o = 54o
∴ Supplement of 54o = 180o – 54o = 126o
-
1o = 60′
⇒ 180o = 179o 60′
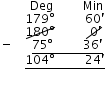
Supplement of 75o 36′ = 180o – 75o 36′ = 104o 24′ (v) 1o = 60′, 1′ = 60″
⇒ 180o = 179o 59′ 60″
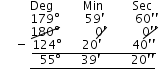
Supplement of 124o 20′ 40″ = 180o – 124o 20′ 40″
= 55o 39′ 20″
(vi) 1o = 60′, 1′ = 60″
⇒ 180o = 179o 59′ 60″

∴ Supplement of 108o 48′ 32″ = 180o – 108o 48′ 32″
= 71o 11′ 28″.
Question 6:
-
-

Let the required angle be xo Then, its complement = 90o – xo
∴ The measure of an angle which is equal to its complement is 45o.
-
-

Let the required angle be xo Then, its supplement = 180o – xo
∴ The measure of an angle which is equal to its supplement is 90o.
Question 7:
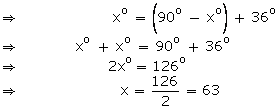
Let the required angle be xo Then its complement is 90o – xo
∴ The measure of an angle which is 36o more than its complement is 63o.
Question 8:

Let the required angle be xo Then its supplement is 180o – xo

∴ The measure of an angle which is 25o less than its supplement is
Question 9:

Let the required angle be xo Then, its complement = 90o – xo
∴ The required angle is 72o.
Question 10:

Let the required angle be xo Then, its supplement is 180o – xo
∴ The required angle is 150o.
Question 11:
Let the required angle be xo
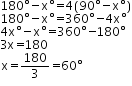
Then, its complement is 90o – xo and its supplement is 180o – xo That is we have,
∴ The required angle is 60o.
Question 12:
Let the required angle be xo

Then, its complement is 90o – xo and its supplement is 180o – xo
∴ The required angle is 45o.
Question 13:
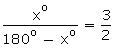
Let the two required angles be xo and 180o – xo. Then,
⇒ 2x = 3(180 – x)
⇒ 2x = 540 – 3x
⇒ 3x + 2x = 540
⇒ 5x = 540
⇒ x = 108
Thus, the required angles are 108o and 180o – xo = 180 o – 108o = 72o.
Question 14:

Let the two required angles be xo and 90o – xo. Then
⇒ 5x = 4(90 – x)
⇒ 5x = 360 – 4x
⇒ 5x + 4x = 360
⇒ 9x = 360
⇒ x =

= 40
Thus, the required angles are 40o and 90o – xo = 90 o – 40o = 50o.
Question 15:
Let the required angle be xo.
Then, its complementary and supplementary angles are (90o – x) and (180o – x) respectively.
Then, 7(90o – x) = 3 (180o – x) – 10o
⇒ 630o – 7x = 540o – 3x – 10o
⇒ 7x – 3x = 630o – 530o
⇒ 4x = 100o
⇒ x = 25o
Thus, the required angle is 25o.
Question 1:
Exercise 4B
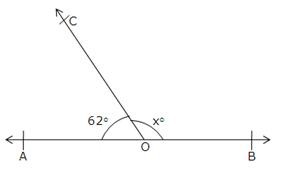
Since ∠BOC and ∠COA form a linear pair of angles, we have
∠BOC + ∠COA = 180o
⇒ xo + 62o = 180o
⇒ x = 180 – 62
∴ x = 118o
Question 2:
Since, ∠BOD and ∠DOA form a linear pair.
∠BOD + ∠DOA = 180o
∴ ∠BOD + ∠DOC + ∠COA = 180o
⇒ (x + 20)o + 55o + (3x – 5)o = 180o
⇒ x + 20 + 55 + 3x – 5 = 180
⇒ 4x + 70 = 180
⇒ 4x = 180 – 70 = 110
⇒ x =

= 27.5
∴ ∠AOC = (3 × 27.5 – 5)o = 82.5-5 = 77.5o And, ∠BOD = (x + 20)o = 27.5o + 20o = 47.5o.
Question 3:
Since ∠BOD and ∠DOA from a linear pair of angles.
⇒ ∠BOD + ∠DOA = 180o
⇒ ∠BOD + ∠DOC + ∠COA = 180o
⇒ xo + (2x – 19)o + (3x + 7)o = 180o
⇒ 6x – 12 = 180
⇒ 6x = 180 + 12 = 192
⇒ x =
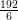
= 32
⇒ x = 32
⇒ ∠AOC = (3x + 7)o = (3 32 + 7)o = 103o
⇒ ∠COD = (2x – 19)o = (2 32 – 19)o = 45o
and ∠BOD = xo = 32o
Question 4:
x: y: z = 5: 4: 6
The sum of their ratios = 5 + 4 + 6 = 15 But x + y + z = 180o
[Since, XOY is a straight line]
So, if the total sum of the measures is 15, then the measure of x is 5. If the sum of angles is 180o, then, measure of x =

× 180 = 60
And, if the total sum of the measures is 15, then the measure of y is 4. If the sum of the angles is 180o, then, measure of y =

× 180 = 48 And ∠z = 180o – ∠x – ∠y
= 180o – 60o – 48o
= 180o – 108o = 72o
∴ x = 60, y = 48 and z = 72.
Question 5:
AOB will be a straight line, if two adjacent angles form a linear pair.
∴ ∠BOC + ∠AOC = 180o
⇒ (4x – 36)o + (3x + 20)o = 180o
⇒ 4x – 36 + 3x + 20 = 180
⇒ 7x – 16 = 180o
⇒ 7x = 180 + 16 = 196
⇒ x =

= 28
∴ The value of x = 28.
Question 6:
Since ∠AOC and ∠AOD form a linear pair.
∴ ∠AOC + ∠AOD = 180o
⇒ 50o + ∠AOD = 180o
⇒ ∠AOD = 180o – 50o = 130o
∠AOD and ∠BOC are vertically opposite angles.
∠AOD = ∠BOC
⇒ ∠BOC = 130o
∠BOD and ∠AOC are vertically opposite angles.
∴ ∠BOD = ∠AOC
⇒ ∠BOD = 50o
Question 7:
Since ∠COE and ∠DOF are vertically opposite angles, we have,
∠COE = ∠DOF
⇒ ∠z = 50o
Also ∠BOD and ∠COA are vertically opposite angles. So, ∠BOD = ∠COA
⇒ ∠t = 90o
As ∠COA and ∠AOD form a linear pair,
∠COA + ∠AOD = 180o
⇒ ∠COA + ∠AOF + ∠FOD = 180o [∠t = 90o]
⇒ t + x + 50o = 180o
⇒ 90o + xo + 50o = 180o
⇒ x + 140 = 180
⇒ x = 180 – 140 = 40
Since ∠EOB and ∠AOF are vertically opposite angles So, ∠EOB = ∠AOF
⇒ y = x = 40
Thus, x = 40 = y = 40, z = 50 and t = 90
Question 8:
Since ∠COE and ∠EOD form a linear pair of angles.
⇒ ∠COE + ∠EOD = 180o
⇒ ∠COE + ∠EOA + ∠AOD = 180o
⇒ 5x + ∠EOA + 2x = 180
⇒ 5x + ∠BOF + 2x = 180
[∴ ∠EOA and BOF are vertically opposite angles so, ∠EOA = ∠BOF]
⇒ 5x + 3x + 2x = 180
⇒ 10x = 180
⇒ x = 18
Now ∠AOD = 2xo = 2 × 18o = 36o
∠COE = 5xo = 5 × 18o = 90o
and, ∠EOA = ∠BOF = 3xo = 3 × 18o = 54o
Question 9:
Let the two adjacent angles be 5x and 4x. Now, since these angles form a linear pair. So, 5x + 4x = 180o
⇒ 9x = 180o
⇒ x =
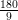
= 20
∴ The required angles are 5x = 5x = 5 20o = 100o and 4x = 4 × 20o = 80o
Question 10:
Let two straight lines AB and CD intersect at O and let ∠AOC = 90o.
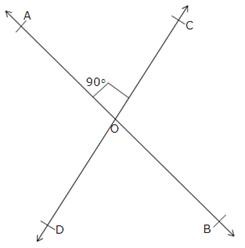
Now, ∠AOC = ∠BOD [Vertically opposite angles]
⇒ ∠BOD = 90o
Also, as ∠AOC and ∠AOD form a linear pair.
⇒ 90o + ∠AOD = 180o
⇒ ∠AOD = 180o – 90o = 90o
Since, ∠BOC = ∠AOD [Verticallty opposite angles]
⇒ ∠BOC = 90o
Thus, each of the remaining angles is 90o.
Question 11:
Since, ∠AOD and ∠BOC are vertically opposite angles.
∴ ∠AOD = ∠BOC
Now, ∠AOD + ∠BOC = 280o [Given]
⇒ ∠AOD + ∠AOD = 280o
⇒ 2∠AOD = 280o
⇒ ∠AOD =

= 140o
⇒ ∠BOC = ∠AOD = 140o
As, ∠AOC and ∠AOD form a linear pair. So, ∠AOC + ∠AOD = 180o
⇒ ∠AOC + 140o = 180o
⇒ ∠AOC = 180o – 140o = 40o
Since, ∠AOC and ∠BOD are vertically opposite angles.
∴ ∠AOC = ∠BOD
⇒ ∠BOD = 40o
∴ ∠BOC = 140o, ∠AOC = 40o , ∠AOD = 140o and ∠BOD = 40o.
Question 12:
Since ∠COB and ∠BOD form a linear pair So, ∠COB + ∠BOD = 180o
⇒ ∠BOD = 180o – ∠COB …. (1)
Also, as ∠COA and ∠AOD form a linear pair. So, ∠COA + ∠AOD = 180o
⇒ ∠AOD = 180o – ∠COA
⇒ ∠AOD = 180o – ∠COB …. (2)
[Since, OC is the bisector of ∠AOB, ∠BOC = ∠AOC] From (1) and (2), we get,
∠AOD = ∠BOD (Proved)
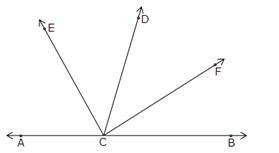
 Question 13:
Question 13:
Let QS be a perpendicular to AB. Now, ∠PQS = ∠SQR
Because angle of incident = angle of reflection
⇒ ∠PQS = ∠SQR =

= 56o
Since QS is perpendicular to AB, ∠PQA and ∠PQS are complementary angles. Thus, ∠PQA + ∠PQS = 90o
⇒ ∠PQA + 56o = 90o
⇒ ∠PQA = 90o – 56o = 34o
Question 14:
Given : AB and CD are two lines which are intersecting at O. OE is a ray bisecting the
∠BOD. OF is a ray opposite to ray OE.

To Prove: ∠AOF = ∠COF
Proof : Since

and

are two opposite rays,
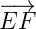
is a straight line passing through O.
∴ ∠AOF = ∠BOE and ∠COF = ∠DOE
[Vertically opposite angles] But ∠BOE = ∠DOE (Given)
∴ ∠AOF = ∠COF
Hence, proved.
Question 15:
Given:

is the bisector of ∠BCD and
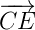
is the bisector of ∠ACD. To Prove: ∠ECF = 90o
Proof: Since ∠ACD and ∠BCD forms a linear pair.
∠ACD + ∠BCD = 180o
∠ACE + ∠ECD + ∠DCF + ∠FCB = 180o
∠ECD + ∠ECD + ∠DCF + ∠DCF = 180o
because ∠ACE = ∠ECD and ∠DCF = ∠FCB
2(∠ECD) + 2 (∠CDF) = 180o
2(∠ECD + ∠DCF) = 180o
∠ECD + ∠DCF =
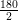
= 90o
∠ECF = 90o (Proved)
Question 1:
Exercise 4C
Since AB and CD are given to be parallel lines and t is a transversal. So, ∠5 = ∠1 = 70o [Corresponding angles are equal]
∠3 = ∠1 = 70o [Vertically opp. Angles]
∠3 + ∠6 = 180o [Co-interior angles on same side]
∴ ∠6 = 180o – ∠3
= 180o – 70o = 110o
∠6 = ∠8 [Vertically opp. Angles]
⇒ ∠8 = 110o
⇒ ∠4 + ∠5 = 180o [Co-interior angles on same side]
∠4 = 180o – 70o = 110o
∠2 = ∠4 = 110o [ Vertically opposite angles]
∠5 = ∠7 [Vertically opposite angles] So, ∠7 = 70o
∴ ∠2 = 110o, ∠3 = 70o , ∠4 = 110o, ∠5 = 70o, ∠6 = 110o, ∠7 = 70o and ∠8 = 110o.
Question 2:
Since ∠2 : ∠1 = 5 : 4.
Let ∠2 and ∠1 be 5x and 4x respectively.
Now, ∠2 + ∠1 = 180o , because ∠2 and ∠1 form a linear pair. So, 5x + 4x = 180o
⇒ 9x = 180o
⇒ x = 20o
∴ ∠1 = 4x = 4 × 20o = 80o And ∠2 = 5x = 5 × 20o = 100o
∠3 = ∠1 = 80o [Vertically opposite angles]
And ∠4 = ∠2 = 100o [Vertically opposite angles]
∠1 = ∠5 and ∠2 = ∠6 [Corresponding angles] So, ∠5 = 80o and ∠6 = 100o
∠8 = ∠6 = 100o [Vertically opposite angles] And ∠7 = ∠5 = 80o [Vertically opposite angles]
Thus, ∠1 = 80o, ∠2 = 100o, ∠3 = ∠80o, ∠4 = 100o, ∠5 = 80o, ∠6 = 100o, ∠7 = 80o and
∠8 = 100o.
Question 3:
Given: AB || CD and AD || BC To Prove: ∠ADC = ∠ABC
Proof: Since AB || CD and AD is a transversal. So sum of consecutive interior angles is
180o.
⇒ ∠BAD + ∠ADC = 180o ….(i)
Also, AD || BC and AB is transversal. So, ∠BAD + ∠ABC = 180o ….(ii) From (i) and (ii) we get:
∠BAD + ∠ADC = ∠BAD + ∠ABC
⇒ ∠ADC = ∠ABC (Proved)
Question 4:
-
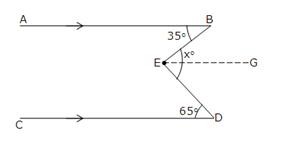
Through E draw EG || CD. Now since EG||CD and ED is a transversal.
So, ∠GED = ∠EDC = 65o [Alternate interior angles] Since EG || CD and AB || CD,
EG||AB and EB is transversal.
So, ∠BEG = ∠ABE = 35o [Alternate interior angles] So, ∠DEB = xo
⇒ ∠BEG + ∠GED = 35o + 65o = 100o.
Hence, x = 100.
-
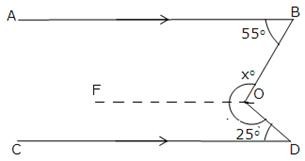
Through O draw OF||CD.
Now since OF || CD and OD is transversal.
∠CDO + ∠FOD = 180o
[sum of consecutive interior angles is 180o]
⇒ 25o + ∠FOD = 180o
⇒ ∠FOD = 180o – 25o = 155o
As OF || CD and AB || CD [Given] Thus, OF || AB and OB is a transversal.
So, ∠ABO + ∠FOB = 180o [sum of consecutive interior angles is 180o]
⇒ 55o + ∠FOB = 180o
⇒ ∠FOB = 180o – 55o = 125o
Now, xo = ∠FOB + ∠FOD = 125o + 155o = 280o.
Hence, x = 280.
-
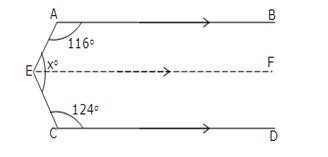
Through E, draw EF || CD.
Now since EF || CD and EC is transversal.
∠FEC + ∠ECD = 180o
[sum of consecutive interior angles is 180o]
⇒ ∠FEC + 124o = 180o
⇒ ∠FEC = 180o – 124o = 56o
Since EF || CD and AB ||CD
So, EF || AB and AE is a trasveral.
So, ∠BAE + ∠FEA = 180o
[sum of consecutive interior angles is 180o]
∴ 116o + ∠FEA = 180o
⇒ ∠FEA = 180o – 116o = 64o
Thus, xo = ∠FEA + ∠FEC
= 64o + 56o = 120o.
Hence, x = 120.
Question 5:
Since AB || CD and BC is a transversal.
So, ∠ABC = ∠BCD [atternate interior angles]
⇒ 70o = xo + ∠ECD ….(i)
Now, CD || EF and CE is transversal.
So, ∠ECD + ∠CEF = 180o
∴ ∠ECD + 130o = 180o
[sum of consecutive interior angles is 180o]
⇒ ∠ECD = 180o – 130o = 50o
Putting ∠ECD = 50o in (i) we get, 70o = xo + 50o
⇒ x = 70 – 50 = 20
Question 6:
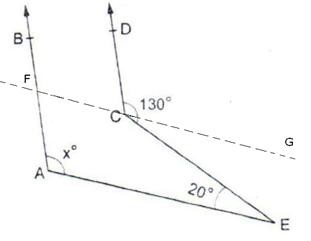
Through C draw FG || AE
Now, since CG || BE and CE is a transversal.
So, ∠GCE = ∠CEA = 20o
∴ ∠DCG = 130o – ∠GCE
= 130o – 20o = 110o
[Alternate angles]
Also, we have AB || CD and FG is a transversal.
So, ∠BFC = ∠DCG = 110o
As, FG || AE, AF is a transversal.
[Corresponding angles]
∠BFG = ∠FAE [Corresponding angles]
∴ xo = ∠FAE = 110o. Hence, x = 110
Question 7:
Given: AB || CD
To Prove: ∠BAE – ∠DCE = ∠AEC
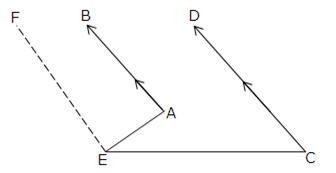
Construction : Through E draw EF || AB Proof : Since EF || AB, AE is a transversal. So, ∠BAE + ∠AEF = 180O ….(i)
[sum of consecutive interior angles is 180o] As EF || AB and AB || CD [Given]
So, EF || CD and EC is a transversal.
So, ∠FEC + ∠DCE = 180o ….(ii)
[sum of consecutive interior angles is 180o] From (i) and (ii) we get,
∠BAE + ∠AEF = ∠FEC + ∠DCE
⇒ ∠BAE – ∠DCE = ∠FEC – ∠AEF = ∠AEC [Proved]
Question 8:
Since AB || CD and BC is a transversal.
So, ∠BCD = ∠ABC = xo
[Alternate angles]
As BC || ED and CD is a transversal.
∠BCD + ∠EDC = 180o
⇒ ∠BCD + 75o =180o
⇒ ∠BCD = 180o – 75o = 105o
∠ABC = 105o
∴ xo = ∠ABC = 105o Hence, x = 105.
[since ∠BCD = ∠ABC]
Question 9:
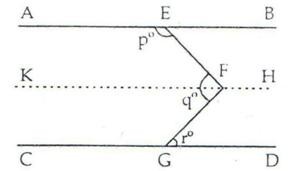
Through F, draw KH || AB || CD
Now, KF || CD and FG is a transversal.
⇒ ∠KFG = ∠FGD = ro …. (i) [alternate angles]
Again AE || KF, and EF is a transversal.
So, ∠AEF + ∠KFE = 180o
∠KFE = 180o – po …. (ii) Adding (i) and (ii) we get,
∠KFG + ∠KFE = 180 – p + r
⇒ ∠EFG = 180 – p + r
⇒ q = 180 – p + r i.e., p + q – r = 180
 Question 10:
Question 10:
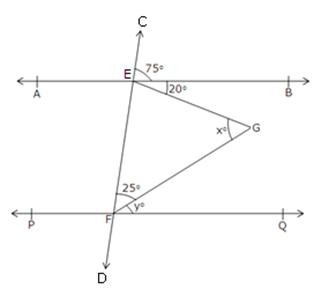
Since AB || PQ and EF is a transversal.
So, ∠CEB = ∠EFQ [Corresponding angles]
⇒ ∠EFQ = 75o
⇒ ∠EFG + ∠GFQ = 75o
⇒ 25o + yo = 75o
⇒ y = 75 – 25 = 50
Also, ∠BEF + ∠EFQ = 180o
∠BEF = 180o – ∠EFQ
= 180o – 75o
∠BEF = 105o
[sum of consecutive interior angles is 180o]
∴ ∠FEG + ∠GEB = ∠BEF = 105o
⇒ ∠FEG = 105o – ∠GEB = 105o – 20o = 85o
In ∆EFG we have,
xo + 25o + ∠FEG = 180o
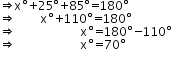
Hence, x = 70.
Question 11:
Since AB || CD and AC is a transversal.
So, ∠BAC + ∠ACD = 180o
⇒ ∠ACD = 180o – ∠BAC
= 180o – 75o = 105o
[sum of consecutive interior angles is 180o]
⇒ ∠ECF = ∠ACD [Vertically opposite angles]
∠ECF = 105o
Now in ∆CEF,
∠ECF + ∠CEF + ∠EFC =180o
⇒ 105o + xo + 30o = 180o
⇒ x = 180 – 30 – 105 = 45
Hence, x = 45.
Question 12:
Since AB || CD and PQ a transversal.
So, ∠PEF = ∠EGH [Corresponding angles]
⇒ ∠EGH = 85o
∠EGH and ∠QGH form a linear pair. So, ∠EGH + ∠QGH = 180o
⇒ ∠QGH = 180o – 85o = 95o
Similarly, ∠GHQ + 115o = 180o
⇒ ∠GHQ = 180o – 115o = 65o
In ∆GHQ, we have, xo + 65o + 95o = 180o
⇒ x = 180 – 65 – 95 = 180 – 160
∴ x = 20
 Question 13:
Question 13:
Since AB || CD and BC is a transversal. So, ∠ABC = ∠BCD
⇒ x = 35
Also, AB || CD and AD is a transversal. So, ∠BAD = ∠ADC
⇒ z = 75
In ∆ABO, we have,
∠AOB + ∠BAO + ∠BOA = 180o
⇒ xo + 75o + yo = 180o
⇒ 35 + 75 + y = 180
⇒ y = 180 – 110 = 70
∴ x = 35, y = 70 and z = 75.
 Question 14:
Question 14:
Since AB || CD and PQ is a transversal. So, y = 75 [Alternate angle]
Since PQ is a transversal and AB || CD, so x + APQ = 180o
[Sum of consecutive interior angles]
⇒ xo = 180o – APQ
⇒ x = 180 – 75 = 105
Also, AB || CD and PR is a transversal.
So, ∠APR = ∠PRD [Alternate angle]
⇒ ∠APQ + ∠QPR = ∠PRD [Since ∠APR = ∠APQ + ∠QPR]
⇒ 75o + zo = 125o
⇒ z = 125 – 75 = 50
∴ x = 105, y = 75 and z = 50.
Question 15:
∠PRQ = xo = 60o
[vertically opposite angles]
Since EF || GH, and RQ is a transversal. So, ∠x = ∠y [Alternate angles]
⇒ y = 60
AB || CD and PR is a transversal.
So, ∠PRD = ∠APR [Alternate angles]
⇒ ∠PRQ + ∠QRD = ∠APR [since ∠PRD = ∠PRQ + ∠QRD]
⇒ x + ∠QRD = 110o
⇒ ∠QRD = 110o – 60o = 50o
In ∆QRS, we have,
∠QRD + to + yo = 180o
⇒ 50 + t + 60 = 180
⇒ t = 180 – 110 = 70
Since, AB || CD and GH is a transversal So, zo = to = 70o [Alternate angles]
∴ x = 60 , y = 60, z = 70 and t = 70
Question 16:
-
Lines l and m will be parallel if 3x – 20 = 2x + 10
[Since, if corresponding angles are equal, lines are parallel]
⇒ 3x – 2x = 10 + 20
⇒ x = 30
-
Lines will be parallel if (3x + 5)o + 4xo = 180o
[if sum of pairs of consecutive interior angles is 180o, the lines are parallel] So, (3x + 5) + 4x = 180
⇒ 3x + 5 + 4x = 180
⇒ 7x = 180 – 5 = 175
⇒ x =
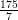
= 25
Question 17:
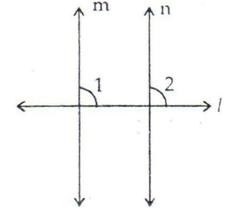
Given: Two lines m and n are perpendicular to a given line l.
To Prove: m || n Proof : Since m ⊥ l So, ∠1 = 90o Again, since n ⊥ l
∠2 = 90o
∴ ∠1 = ∠2 = 90o
But ∠1 and ∠2 are the corresponding angles made by the transversal l with lines m and n and they are proved to be equal.
Thus, m || n.
Question 1:
Exercise 4D
Since, sum of the angles of a triangle is 180o
∠A + ∠B + ∠C = 180o
⇒ ∠A + 76o + 48o = 180o
⇒ ∠A = 180o – 124o = 56o
∴ ∠A = 56o
Question 2:
Let the measures of the angles of a triangle are (2x)o, (3x)o and (4x)o. Then, 2x + 3x + 4x = 180 [sum of the angles of a triangle is 180o ]
⇒ 9x = 180
⇒ x =

= 20
∴ The measures of the required angles are: 2x = (2 × 20)o = 40o
3x = (3 × 20)o = 60o
4x = (4 × 20)o = 80o
Question 3:
Let 3∠A = 4∠B = 6∠C = x (say) Then, 3∠A = x
⇒ ∠A =
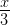
4∠B = x
⇒ ∠B =
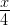
and 6∠C = x
⇒ ∠C =

As ∠A + ∠B + ∠C = 180o
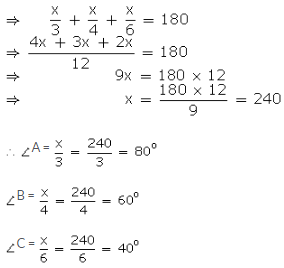
Question 4:
∠A + ∠B = 108o [Given]
But as ∠A, ∠B and ∠C are the angles of a triangle,
∠A + ∠B + ∠C = 180o
⇒ 108o + ∠C = 180o
⇒ C = 180o – 108o = 72o
Also, ∠B + ∠C = 130o [Given]
⇒ ∠B + 72o = 130o
⇒ ∠B = 130o – 72o = 58o Now as, ∠A + ∠B = 108o
⇒ ∠A + 58o = 108o
⇒ ∠A = 108o – 58o = 50o
∴ ∠A = 50o, ∠B = 58o and ∠C = 72o.
Question 5:
Since. ∠A , ∠B and ∠C are the angles of a triangle . So, ∠A + ∠B + ∠C = 180o
Now, ∠A + ∠B = 125o [Given]
∴ 125o + ∠C = 180o
⇒ ∠C = 180o – 125o = 55o
Also, ∠A + ∠C = 113o [Given]
⇒ ∠A + 55o = 113o
⇒ ∠A = 113o – 55o = 58o Now as ∠A + ∠B = 125o
⇒ 58o + ∠B = 125o
⇒ ∠B = 125o – 58o = 67o
∴ ∠A = 58o, ∠B = 67o and ∠C = 55o.
Question 6:
Since, ∠P, ∠Q and ∠R are the angles of a triangle. So, ∠P + ∠Q + ∠R = 180o ….(i)
Now, ∠P – ∠Q = 42o [Given]
⇒ ∠P = 42o + ∠Q ….(ii)
and ∠Q – ∠R = 21o [Given]
⇒ ∠R = ∠Q – 21o ….(iii)
Substituting the value of ∠P and ∠R from (ii) and (iii) in (i), we get,
⇒ 42o + ∠Q + ∠Q + ∠Q – 21o = 180o
⇒ 3∠Q + 21o = 180o
⇒ 3∠Q = 180o – 21o = 159o
∠Q =
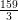
= 53o
∴ ∠P = 42o + ∠Q
= 42o + 53o = 95o
∠R = ∠Q – 21o
= 53o – 21o = 32o
∴ ∠P = 95o, ∠Q = 53o and ∠R = 32o.
Question 7:
Given that the sum of the angles A and B of a ABC is 116o, i.e., ∠A + ∠B = 116o. Since, ∠A + ∠B + ∠C = 180o
So, 116o + ∠C = 180o
⇒ ∠C = 180o – 116o = 64o
Also, it is given that:
∠A – ∠B = 24o
⇒ ∠A = 24o + ∠B
Putting, ∠A = 24o + ∠B in ∠A + ∠B = 116o, we get,
⇒ 24o + ∠B + ∠B = 116o
⇒ 2∠B + 24o = 116o
⇒ 2∠B = 116o – 24o = 92o
∠B =
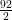
= 46o
Therefore, ∠A = 24o + 46o = 70o
∴ ∠A = 70o, ∠B = 46o and ∠C = 64o.
Question 8:
Let the two equal angles, A and B, of the triangle be xo each. We know,
∠A + ∠B + ∠C = 180o
⇒ xo + xo + ∠C = 180o
⇒ 2xo + ∠C = 180o ….(i) Also, it is given that,
∠C = xo + 18o ….(ii)
Substituting ∠C from (ii) in (i), we get,
⇒ 2xo + xo + 18o = 180o
⇒ 3xo = 180o – 18o = 162o x =

= 54o
Thus, the required angles of the triangle are 54o, 54o and xo + 18o = 54o + 18o = 72o.
Question 9:
Let ∠C be the smallest angle of ABC. Then, ∠A = 2∠C and B = 3∠C
Also, ∠A + ∠B + ∠C = 180o
⇒ 2∠C + 3∠C + ∠C = 180o
⇒ 6∠C = 180o
⇒ ∠C = 30o
So, ∠A = 2∠C = 2 (30o) = 60o
∠B = 3∠C = 3 (30o) = 90o
∴ The required angles of the triangle are 60o, 90o, 30o.
Question 10:
Let ABC be a right angled triangle and ∠C = 90o Since, ∠A + ∠B + ∠C = 180o
⇒ ∠A + ∠B = 180o – ∠C = 180o – 90o = 90o
Suppose ∠A = 53o
Then, 53o + ∠B = 90o
⇒ ∠B = 90o – 53o = 37o
∴ The required angles are 53o, 37o and 90o.
Question 11:
Let ABC be a triangle. Given, ∠A + ∠B = ∠C
We know, ∠A + ∠B + ∠C = 180o
⇒ ∠C + ∠C = 180o
⇒ 2∠C = 180o
⇒ ∠C =
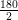
= 90o
So, we find that ABC is a right triangle, right angled at C.
Question 12:
Given : ∆ABC in which ∠A = 90o, AL ⊥ BC To Prove: ∠BAL = ∠ACB
Proof :
In right triangle ∆ABC,
⇒ ∠ABC + ∠BAC + ∠ACB = 180o
⇒ ∠ABC + 90o + ∠ACB = 180o
⇒ ∠ABC + ∠ACB = 180o – 90o
∴ ∠ABC + ∠ACB = 90o
⇒ ∠ ACB = 90o – ∠ABC ….(1)
Similarly since ∆ABL is a right triangle, we find that,
∠BAL = 90o – ∠ABC …(2)
Thus from (1) and (2), we have
∴ ∠BAL = ∠ACB (Proved)
Question 13:
Let ABC be a triangle. So, ∠A < ∠B + ∠C
Adding A to both sides of the inequality,
⇒ 2∠A < ∠A + ∠B + ∠C
⇒ 2∠A < 180o
⇒ ∠A <
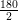
= 90o
[Since ∠A + ∠B + ∠C = 180o]
Similarly, ∠B < ∠A + ∠C
⇒ ∠B < 90o
and ∠C < ∠A + ∠B
⇒ ∠C < 90o
∆ABC is an acute angled triangle.
Question 14:
Let ABC be a triangle and ∠B > ∠A + ∠C Since, ∠A + ∠B + ∠C = 180o
⇒ ∠A + ∠C = 180o – ∠B Therefore, we get
∠B > 180o – ∠B
Adding ∠B on both sides of the inequality, we get,
⇒ ∠B + ∠B > 180o – ∠B + ∠B
⇒ 2∠B > 180o
⇒ ∠B >
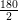
= 90o
i.e., ∠B > 90o which means ∠B is an obtuse angle.
∆ABC is an obtuse angled triangle.
Question 15:
Since ∠ACB and ∠ACD form a linear pair. So, ∠ACB + ∠ACD = 180o
⇒ ∠ACB + 128o = 180o
⇒ ∠ACB = 180o – 128 = 52o
Also, ∠ABC + ∠ACB + ∠BAC = 180o
⇒ 43o + 52o + ∠BAC = 180o
⇒ 95o + ∠BAC = 180o
⇒ ∠BAC = 180o – 95o = 85o
∴ ∠ACB = 52o and ∠BAC = 85o.
Question 16:
As ∠DBA and ∠ABC form a linear pair. So, ∠DBA + ∠ABC = 180o
⇒ 106o + ∠ABC = 180o
⇒ ∠ABC = 180o – 106o = 74o
Also, ∠ACB and ∠ACE form a linear pair. So, ∠ACB + ∠ACE = 180o
⇒ ∠ACB + 118o = 180o
⇒ ∠ACB = 180o – 118o = 62o
In ∠ABC, we have,
∠ABC + ∠ACB + ∠BAC = 180o 74o + 62o + ∠BAC = 180o
⇒ 136o + ∠BAC = 180o
⇒ ∠BAC = 180o – 136o = 44o
∴ In triangle ABC, ∠A = 44o, ∠B = 74o and ∠C = 62o
Question 17:
(i) ∠EAB + ∠BAC = 180o [Linear pair angles]

110o + ∠BAC = 180o
⇒ ∠BAC = 180o – 110o = 70o
Again, ∠BCA + ∠ACD = 180o [Linear pair angles]
⇒ ∠BCA + 120o = 180o
⇒ ∠BCA = 180o – 120o = 60o
Now, in ∆ABC,
∠ABC + ∠BAC + ∠ACB = 180o
xo + 70o + 60o = 180o
⇒ x + 130o = 180o
⇒ x = 180o – 130o = 50o
∴ x = 50 (ii)
In ∆ABC,
∠A + ∠B + ∠C = 180o
⇒ 30o + 40o + ∠C = 180o
⇒ 70o + ∠C = 180o
⇒ ∠C = 180o – 70o = 110o
Now ∠BCA + ∠ACD = 180o [Linear pair]
⇒ 110o + ∠ACD = 180o
⇒ ∠ACD = 180o – 110o = 70o In ∆ECD,
⇒ ∠ECD + ∠CDE + ∠CED = 180o
⇒ 70o + 50o + ∠CED = 180o
⇒ 120o + ∠CED = 180o
∠CED = 180o – 120o = 60o
Since ∠AED and ∠CED from a linear pair So, ∠AED + ∠CED = 180o
⇒ xo + 60o = 180o
⇒ xo = 180o – 60o = 120o
∴ x = 120 (iii)
∠EAF = ∠BAC [Vertically opposite angles]
⇒ ∠BAC = 60o
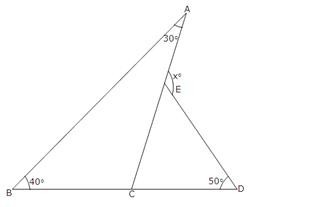
In ∆ABC, exterior ∠ACD is equal to the sum of two opposite interior angles. So, ∠ACD = ∠BAC + ∠ABC
⇒ 115o = 60o + xo
⇒ xo = 115o – 60o = 55o
∴ x = 55 (iv)

Since AB || CD and AD is a transversal. So, ∠BAD = ∠ADC
⇒ ∠ADC = 60o
In ∠ECD, we have,
∠E + ∠C + ∠D = 180o
⇒ xo + 45o + 60o = 180o
⇒ xo + 105o = 180o
⇒ xo = 180o – 105o = 75o
∴ x = 75 (v)
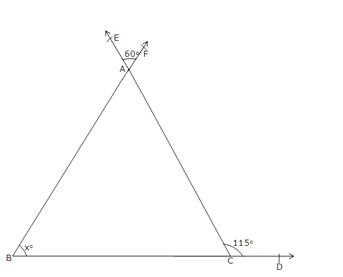
In ∆AEF,
Exterior ∠BED = ∠EAF + ∠EFA
⇒ 100o = 40o + ∠EFA
⇒ ∠EFA = 100o – 40o = 60o
Also, ∠CFD = ∠EFA [Vertically Opposite angles]
⇒ ∠CFD = 60o Now in ∆FCD,
Exterior ∠BCF = ∠CFD + ∠CDF
⇒ 90o = 60o + xo
⇒ xo = 90o – 60o = 30o
∴ x = 30 (vi)

In ∆ABE, we have,
∠A + ∠B + ∠E = 180o
⇒ 75o + 65o + ∠E = 180o
⇒ 140o + ∠E = 180o
⇒ ∠E = 180o – 140o = 40o
Now, ∠CED = ∠AEB [Vertically opposite angles]
⇒ ∠CED = 40o
Now, in ∆CED, we have,
∠C + ∠E + ∠D = 180o
⇒ 110o + 40o + xo = 180o
⇒ 150o + xo = 180o
⇒ xo = 180o – 150o = 30o
∴ x = 30
Question 18:

Produce CD to cut AB at E.
Now, in ∆BDE, we have,
Exterior ∠CDB = ∠CEB + ∠DBE
⇒ xo = ∠CEB + 45o In ∆AEC, we have,
…..(i)
Exterior ∠CEB = ∠CAB + ∠ACE
= 55o + 30o = 85o
Putting ∠CEB = 85o in (i), we get, xo = 85o + 45o = 130o
∴ x = 130
Question 19:
The angle ∠BAC is divided by AD in the ratio 1 : 3. Let ∠BAD and ∠DAC be y and 3y, respectively. As BAE is a straight line,
∠BAC + ∠CAE = 180o
[linear pair]
⇒ ∠BAD + ∠DAC + ∠CAE = 180o
⇒ y + 3y + 108o = 180o
⇒ 4y = 180o – 108o = 72o
⇒ y =

= 18o Now, in ∆ABC,
∠ABC + ∠BCA + ∠BAC = 180o
y + x + 4y = 180o
[Since, ∠ABC = ∠BAD (given AD = DB) and ∠BAC = y + 3y = 4y]
⇒ 5y + x = 180
⇒ 5 × 18 + x = 180
⇒ 90 + x = 180
∴ x = 180 – 90 = 90
Question 20:
Given : A ∆ABC in which BC, CA and AB are produced to D, E and F respectively. To prove : Exterior ∠DCA + Exterior ∠BAE + Exterior ∠FBD = 360o
Proof : Exterior ∠DCA = ∠A + ∠B ….(i) Exterior ∠FAE = ∠B + ∠C ….(ii) Exterior ∠FBD = ∠A + ∠C ….(iii) Adding (i), (ii) and (iii), we get,
Ext. ∠DCA + Ext. ∠FAE + Ext. ∠FBD
= ∠A + ∠B + ∠B + ∠C + ∠A + ∠C
= 2∠A + 2∠B + 2∠C
= 2 (∠A + ∠B + ∠C)
= 2 × 180o
[Since, in triangle the sum of all three angle is 180o]
= 360o
Hence, proved.
Question 21:
In ∆ACE, we have,
∠A + ∠C + ∠E = 180o ….(i) In ∆BDF, we have,
∠B + ∠D + ∠F = 180o ….(ii)
Adding both sides of (i) and (ii), we get,
∠A + ∠C +∠E + ∠B + ∠D + ∠F = 180o + 180o
⇒ ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 360o.
Question 22:
Given : In ∆ABC, bisectors of ∠B and ∠C meet at O and ∠A = 70o In ∆BOC, we have,
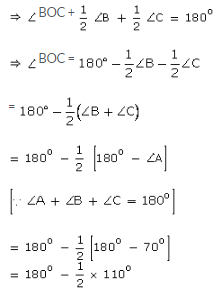
∠BOC + ∠OBC + ∠OCB = 180o
= 180o – 55o = 125o
∴ ∠BOC = 125o.
Question 23:
We have a ∆ABC whose sides AB and AC have been procued to D and E. A = 40o and bisectors of ∠CBD and ∠BCE meet at O.
In ∆ABC, we have, Exterior ∠CBD = C + 40o
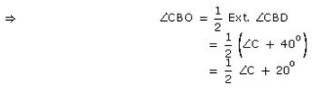
And exterior ∠BCE = B + 40o
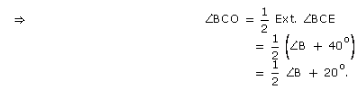
Now, in ∆BCO, we have,
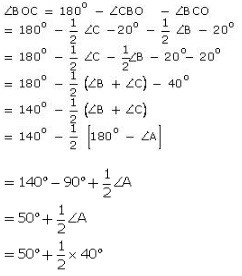
= 50o + 20o
= 70o
Thus, ∠BOC = 70o
Question 24:
In the given ∆ABC, we have,
∠A : ∠B : ∠C = 3 : 2 : 1
Let ∠A = 3x, ∠B = 2x, ∠C = x. Then,
∠A + ∠B + ∠C = 180o
⇒ 3x + 2x + x = 180o
⇒ 6x = 180o
⇒ x = 30o
∠A = 3x = 3 30o = 90o
∠B = 2x = 2 30o = 60o
and, ∠C = x = 30o
Now, in ∆ABC, we have,
Ext ∠ACE = ∠A + ∠B = 90o + 60o = 150o
∠ACD + ∠ECD = 150o
⇒ ∠ECD = 150o – ∠ACD
⇒ ∠ECD = 150o – 90o
⇒ ∠ECD= 60o
[since , AD ⊥ CD, ∠ACD = 90o]
Question 25:
In ∆ABC, AN is the bisector of ∠A and AM ⊥ BC. Now in ∆ABC we have;
∠A = 180o – ∠B – ∠C
⇒ ∠A = 180o – 65o – 30o
= 180o – 95o
= 85o
Now, in ∆ANC we have;

Thus, ∠MAN =
Question 26:
(i) False (ii) True (iii) False (iv) False (v) True (vi) True.
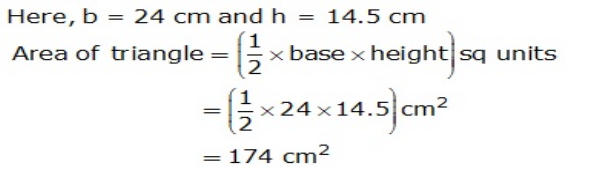




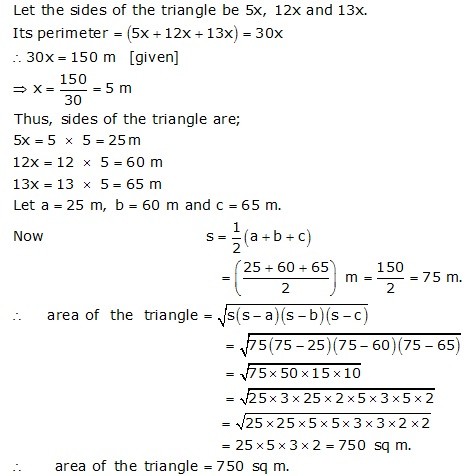







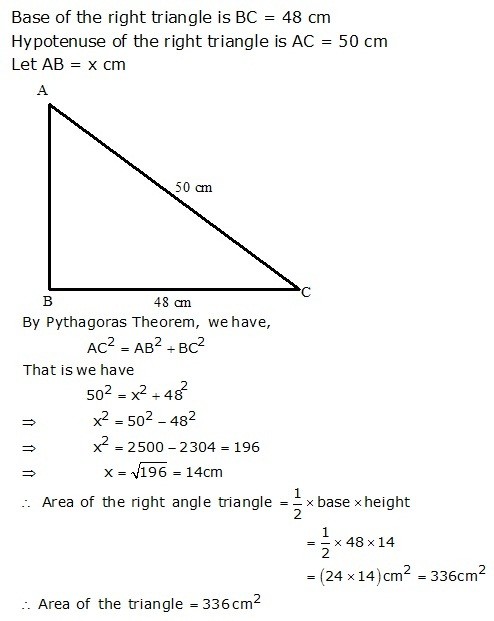
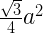











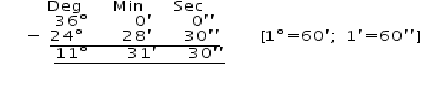
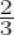
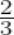



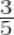
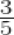





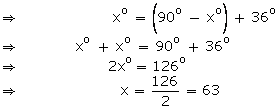




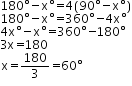

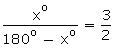




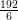



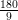


 Question 13:
Question 13:





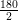






 Question 10:
Question 10: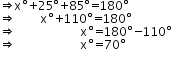
 Question 13:
Question 13: Question 14:
Question 14: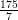


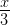
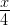


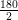
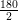
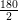








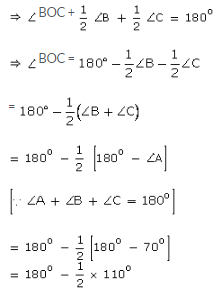
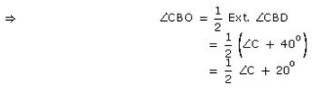
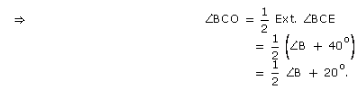
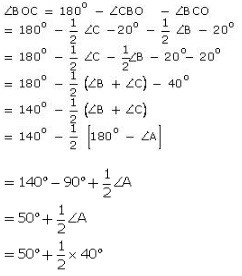

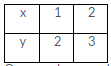













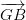



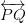
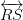

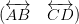
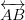



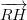
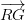


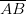




 , where p and q are integers and q ≠ 0 are known as rational numbers.
, where p and q are integers and q ≠ 0 are known as rational numbers.


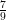



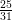









 (vi) -2.4
(vi) -2.4

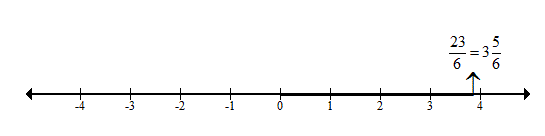

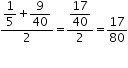
 A rational number lying between
A rational number lying between
 and
and
 is
is

 <
<
 <
<
 <
<
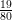 <
<
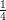 Or we can say that,
Or we can say that,
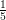 <
<
 <
<
 <
<
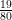 <
<
 That is,
That is,
 <
<
 <
<
 <
<
 <
<

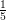 and
and
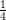 are
are



 and
and

 <
<

 That is,
That is,
 <
<
 .
.
 <
<
 <
<
 <
<
 <
<
 <
<
 <
<
 <
<
 Thus, 5 rational numbers between,
Thus, 5 rational numbers between,
 <
<
 are:
are:
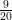

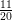
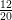
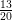
 <
<
 .
.
 <
<
 <
<
 <
<
 <
<
 <
<
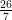 <
<
 <
<
 Therefore, 6 rational numbers between 3 and 4 are:
Therefore, 6 rational numbers between 3 and 4 are:


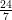


 <
<
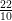 Or,
Or,
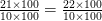
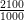 <
<
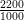
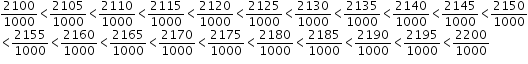 Therefore, we can have,
Therefore, we can have,

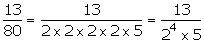 (i)
(i)

 is a terminating decimal.
is a terminating decimal.
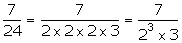 (ii)
(ii)

 is not a terminating decimal.
is not a terminating decimal.
 (iii)
(iii)

 is not a terminating decimal.
is not a terminating decimal.
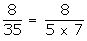 (iv)
(iv)

 is not a terminating decimal.
is not a terminating decimal.
 (v)
(v)

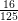 is a terminating decimal.
is a terminating decimal.
 Question 2:
Question 2: (i)
(i)
 = 0.625
= 0.625
 (ii)
(ii)
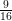
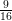 = 0.5625
= 0.5625
 (iii)
(iii)

 = 0.28
= 0.28

 (iv)
(iv)
 = 0.458
= 0.458


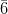 (v)
(v)

 = 2.41
= 2.41

 ⇒ x =
⇒ x =
 =
=
 Hence, 0. =
Hence, 0. =
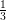
 Let x = 1.
Let x = 1.
 =
=

 Hence, 1. =
Hence, 1. =

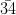 Let x = 0.
Let x = 0.

 Hence, 0. =
Hence, 0. =

 Let x = 3.
Let x = 3.

 Hence, 3. =
Hence, 3. =

 Let x = 0.
Let x = 0.
 =
=

 Hence, 0. =
Hence, 0. =

 Let x = 0.
Let x = 0.
 =
=

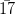 Hence, 0. =
Hence, 0. =
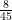
 Let x = 0.
Let x = 0.

 Hence, 0. =
Hence, 0. =
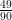
 (vii) Let x = Let x = 0.1 i.e. x = 0.16363 …. (i)
(vii) Let x = Let x = 0.1 i.e. x = 0.16363 …. (i)
 ⇒ x =
⇒ x =
 =
=
 Hence, 0.1 =
Hence, 0.1 =
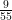
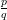 , p and q are integers and q ≠ 0, may not be a whole number.
, p and q are integers and q ≠ 0, may not be a whole number.
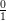 , which is a rational number.
, which is a rational number.
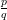 , p and q are integers and q ≠ 0
, p and q are integers and q ≠ 0
 etc are examples of irrational numbers.
etc are examples of irrational numbers.

 is a rational number. Here, 4 is a perfect square and hence,
is a rational number. Here, 4 is a perfect square and hence,
 = 2 is a rational number. So,
= 2 is a rational number. So,
 is a rational number.
is a rational number.
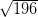
 is a rational number. Here, 196 is a perfect square and hence
is a rational number. Here, 196 is a perfect square and hence
 is a rational number. So,
is a rational number. So,
 is rational.
is rational.

 is an irrational number. Here, 21 is a not a perfect square number and hence,
is an irrational number. Here, 21 is a not a perfect square number and hence,
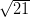 is an irrational number. So,
is an irrational number. So,
 is irrational.
is irrational.
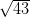
 is an irrational number. Here, 43 is not a perfect square number and hence,
is an irrational number. Here, 43 is not a perfect square number and hence,
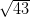 is an irrational number. So,
is an irrational number. So,
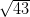 is irrational.
is irrational.

 , is the sum of a rational number 3 and
, is the sum of a rational number 3 and
 irrational number .
irrational number .
 , is an irrational number.
, is an irrational number.

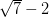 =
=
 + (-2) is the sum of a rational number and an irrational number.
+ (-2) is the sum of a rational number and an irrational number.
 + (-2) , is an irrational number.
+ (-2) , is an irrational number.
 is irrational.
is irrational.

 =
=
 ×
×
 is the product of a rational number and an irrational number .
is the product of a rational number and an irrational number .
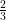 ×
×
 is an irrational number.
is an irrational number.
 is an irrational number.
is an irrational number.
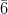 0.
0.
 = 0.6666
= 0.6666
 Question 3:
Question 3:
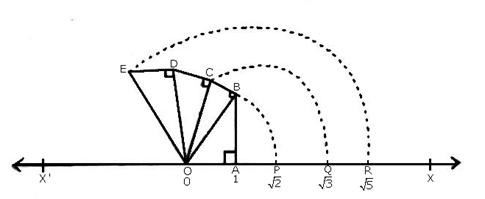
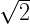 units
units
 on the real line.
on the real line.
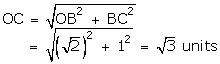
 units
units
 on the real line. Now draw CD ⊥ OC such that CD = 1 units
on the real line. Now draw CD ⊥ OC such that CD = 1 units
 Join OD. Then,
Join OD. Then,

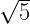 units
units
 on the real line.
on the real line.
 Question 4:
Question 4: Join OB. Then,
Join OB. Then,
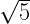
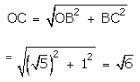

 on the real line. Now, draw CD ⊥ OC as set off CD = 1 units Join OD. Then,
on the real line. Now, draw CD ⊥ OC as set off CD = 1 units Join OD. Then,


 on the real line.
on the real line.
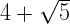
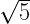 is an irrational number.
is an irrational number.
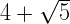 is irrational because sum of a rational number and irrational number is always an irrational number.
is irrational because sum of a rational number and irrational number is always an irrational number.
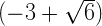
 is irrational.
is irrational.
 is irrational because sum of a rational number and irrational number is always an irrational number.
is irrational because sum of a rational number and irrational number is always an irrational number.

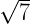 is an irrational number.
is an irrational number.
 is irrational because product of a rational number and an irrational number is always irrational.
is irrational because product of a rational number and an irrational number is always irrational.
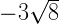
 is an irrational number.
is an irrational number.
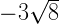 is irrational because product of a rational number and an irrational number is always irrational.
is irrational because product of a rational number and an irrational number is always irrational.
 (v)
(v)

 is irrational because it is the product of a rational number and the irrational number
is irrational because it is the product of a rational number and the irrational number
 .
.
 (vi)
(vi)
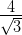
 is an irrational number because it is the product of rational number and irrational number
is an irrational number because it is the product of rational number and irrational number
 .
.
 (i)
(i)

 (ii)
(ii)


 Question 2:
Question 2:
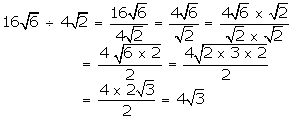 (i)
(i)
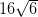 by
by

 by
by


 (iii)
(iii)
 by
by


 Question 5:
Question 5:
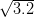 units.
units.
 units.
units.
 Question 6:
Question 6: units.
units.
 units.
units.
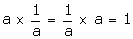 For each non zero real number a, there exists a real number
For each non zero real number a, there exists a real number
 such that
such that
 are called the multiplicative inverse of each other.
are called the multiplicative inverse of each other.
 On multiplying the numerator and denominator of the given number by
On multiplying the numerator and denominator of the given number by
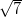 , we get
, we get
 On multiplying the numerator and denominator of the given number by
On multiplying the numerator and denominator of the given number by
 , we get
, we get
 Question 3:
Question 3: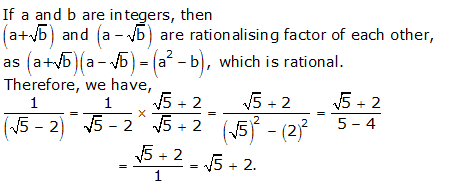 Question 4:
Question 4:

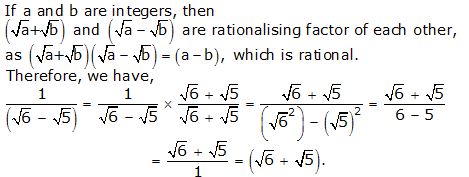 Question 6:
Question 6:
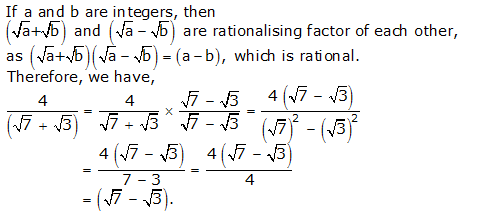 Question 7:
Question 7:
 Question 8:
Question 8:

 Question 10:
Question 10:
 Question 11:
Question 11:
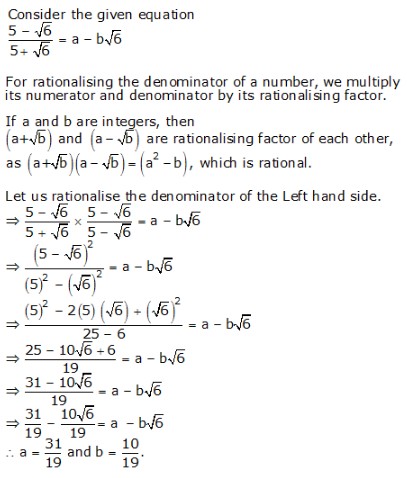
 Question 13:
Question 13:


 Question 16:
Question 16:

 Question 18:
Question 18:
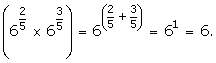 (i)
(i)

 (iii)
(iii)
 (i)
(i)
 (ii)
(ii)

 (i)
(i)

 (iii)
(iii)
 (i)
(i)

 (iii)
(iii)
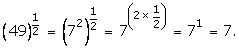 (i)
(i)
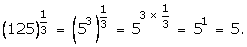
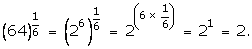 (iii)
(iii)
 (i)
(i)
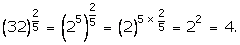
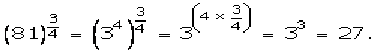
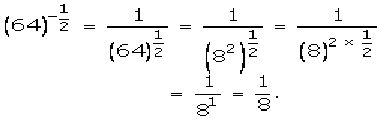 (i)
(i)

 (iii)
(iii)