Category: Maths

Chapter 9 Areas of Parallelograms and Triangles

1. Figures on the same Base and Between the same Parallels
2. Parallelograms on the same Base and between the same Parallels
3. Triangles on the same Base and between the same Parallels

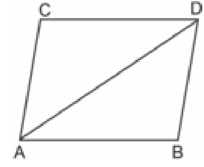
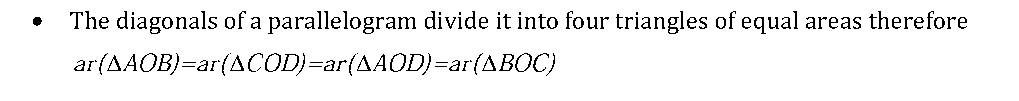
• If a parallelogram and a triangle are on the same base and between the same parallel, then

area of the triangle is equal to one half area of the parallelogram.

• A median AD of a AABC divides it into two triangles of equal areas. Therefore ar(AABD)=ar(ACD )
• If the medians of a intersect at G, then ar(AAGB)=ar(AAGC )=ar(ABGC )=1 ar (AABC)

• Triangles with equal bases and equal areas have equal corresponding altitude.

Chapter – 7 Triangles

1. Congruence of Triangles
2. Criteria for Congruence of Triangles
3. Some Properties of a Triangle
4. Inequalities in a Triangle

• Triangle- A closed figure formed by three intersecting lines is called a triangle. A triangle has three sides, three angles and three vertices.
• Congruent figures- Congruent means equal in all respects or figures whose shapes and sizes are both the same for example, two circles of the same radii are congruent. Also two squares of the same sides are congruent.
• Congruent Triangles- two triangles are congruent if and only if one of them can be made to superpose on the other, so as to cover it exactly.

• If two triangles ABC and PQR are congruent under the correspondence A « P, B « Q and C « R then symbolically, it is expressed as DABC @ DPQR

• In congruent triangles corresponding parts are equal and we write ‘CPCT’ for corresponding parts of congruent triangles.

• SAS congruency rule – Two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle. For example: DABC and DPQR as shown in the figure satisfy SAS congruent criterion.

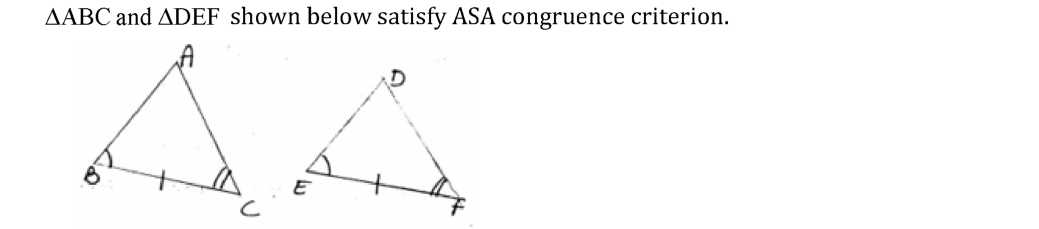
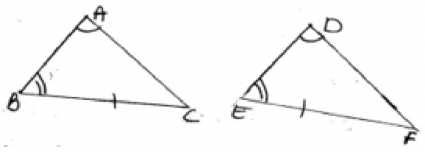
• ASA Congruence Rule- Two triangles are congruent if two angles and the included side of

one triangle are equal to two angles and the included side of other triangle. For examples

• AAS Congruence Rule- Two triangle are congruent if any two pairs of angles and one pair of corresponding sides are equal for example DABC and DDEF shown below satisfy AAS
• Angle opposite to equal sides of a triangle are equal.

congruence criterion.

• AAS criterion for congruence of triangles is a particular case of ASA criterion.
• Isosceles Triangle- A triangle in which two sides are equal is called an isosceles triangle.

• Sides opposite to equal angles of a triangle are equal.
• Each angle of an equilateral triangle is 60^o.
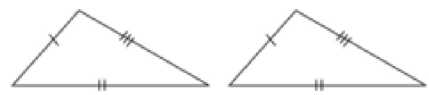
• SSS congruence Rule – If three sides of one triangle are equal to the three sides of another triangle then the two triangles are congruent for example DABC and DDEF as shown in

the figure satisfy SSS congruence criterion.

• RHS Congruence Rule- If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle then the two triangle are congruent. For example: DABCand DPQR shown below satisfy RHS

congruence criterion.

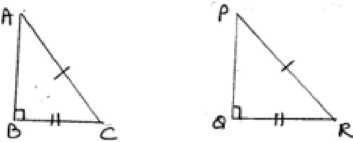
RHS stands for right angle – Hypotenuse side.

• A point equidistant from two given points lies on the perpendicular bisector of the line segment joining the two points and its converse.
• A point equidistant from two intersecting lines lies on the bisectors of the angles formed by the two lines.
• In a triangle, angle opposite to the longer side is larger (greater)
• In a triangle, side opposite to the large (greater) angle is longer.
• Sum of any two sides of a triangle is greater than the third side.

Chapter – 6 Lines and Angles

1. Basic Terms and Definitions
2. Intersecting Lines and Non-Intersecting Lines
3. Pairs of Angles
4. Parallel Lines and a Transversal
5. Lines Parallel to the same Line
6. Angle Sum Property of a Triangle
7. Point- We often represent a point by a fine dot made with a fine sharpened pencil on a piece of paper.
8. Line- A line is completely known if we are given any two distinct points. Line AB is represented by as AB . A line or a straight line extends indefinitely in both the directions.

(5) Collinear points- If three or more points lie on the same line, they are called collinear points otherwise they are called non-collinear points.

Types of Angles-

1. Acute angle- An acute angle measure between O^o and 90^o
2. Right angle- A right angle is exactly equal to 90^o
3. Obtuse angle- An angle greater than 90^o but less than 180^o
4. Straight angle- A straight angle is equal to 180^o
5. Reflex angle- An angle which is greater than 180^o but less than 360^o is called a reflex angle.
6. Complementary angles- Two angles whose sum is 90^o are called complementary angles.
7. Supplementary angle- Two angles whose sum is 180^o are called supplementary angles.
8. Adjacent angles- Two angles are adjacent, if they have a common vertex, a common arm and their non-common arms are on different sides of common arm.
9. Linear pair- Two angles form a linear pair, if their non-common arms form a line.
10. Vertically opposite angles- Vertically opposite angles are formed when two lines intersect each other at a point.

TRANSVERSAL:

1. Corresponding angles
2. Alternate interior angles
3. Alternate exterior angles
4. Interior angles on the same side of the transversal.

• If a transversal intersects two parallel lines, then

1. each pair of corresponding angles is equal.
2. each pair of alternate interior angles is equal.
3. each pair of interior angle on the same side of the transversal is supplementary.

• If a transversal interacts two lines such that, either

1. any one pair of corresponding angles is equal, or
2. any one pair of alternate interior angles is equal or

(iii) any one pair of interior angles on the same side of the transversal is supplementary then the lines are parallel.

• Lines which are parallel to a given line are parallel to each other.
• The sum of the three angles of a triangle is 180°
• If a side of a triangle is produced, the exterior angle so formed is equal to the sum of the two interior opposite angles.

Chapter – 3 Coordinate Geometry

1. Cartesian System
2. Plotting a Point in the Plane with given Coordinates

• Coordinate Geometry: The branch of mathematics in which geometric problems are solved

through algebra by using the coordinate system is known as coordinate geometry.

• Coordinate System: Coordinate axes: The position of a point in a plane is determined with

reference to two fixed mutually perpendicular lines, called the coordinate axes.

In this system, position of a point is described by ordered pair of two numbers.

Ordered pair: A pair of numbers a and b listed in a specific order with ‘a’ at the first place and ‘b’ at the second place is called an ordered pair (a,b)

Note that (a,b) ^ (b,a)

Thus (2,3) is one ordered pair and (3,2) is another ordered pair.

In given figure O is called origin.

The horizontal line X1 OX is called the X-axis.

The vertical line YOY’ is called the Y-axis.

P(a,b) be any point in the plane. ‘a’ the first number denotes the distance of point from Y-axis and ‘b’ the second number denotes the distance of point from X-axis. a – X – coordinate | abscissa of P. b – Y – coordinate | ordinate of P.

The coordinates of origin are (0,0)

Every point on the x-axis is at a distance o unit from the X-axis. So its ordinate is 0.

Every point on the y-axis is at a distance of unit from the Y-axis. So, its abscissa is 0.

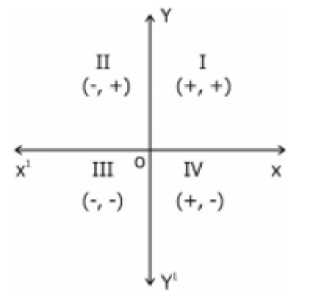
Note: Any point lying on X – axis or Y – axis Y-axis does not lie in any quadrant.

CHAPTER – 2 POLYNOMIAL

1. Polynomials in one Variable
2. Zeroes of a Polynomial
3. Remainder Theorem
4. Factorisation of Polynomials
5. Algebraic Identities

• Constants: A symbol having a fixed numerical value is called a constant.
• Variables: A symbol which may be assigned different numerical values is known as variable.
• Algebraic expressions: A combination of constants and variables. Connected by some or all of the operations +, -, X and is known as algebraic expression.
• Terms: The several parts of an algebraic expression separated by ‘+’ or ‘-‘ operations are called the terms of the expression.
• Polynomials: An algebraic expression in which the variables involved have only nonnegative integral powers is called a polynomial.

1. 5x² – 4x² – 6x – 3 is a polynomial in variable x.

3

1. (ii) 5 + 8x² + 4x^-2 is an expression but not a polynomial.

Polynomials are denoted by p(x), q(x) and r(x)etc.

• Coefficients: In the polynomial x³ + 3x² + 3x +1, coefficient of x³, x², x are1,3,3 respectively

and we also say that +1 is the constant term in it.

• Degree of a polynomial in one variable: In case of a polynomial in one variable the highest

power of the variable is called the degree of the polynomial.

• Classification of polynomials on the basis of degree.

Degree Polynomial Example

1. 1 Linear x +1, 2x + 3etc.
2. 2 Quadratic ax² + bx + c etc.
3. 3 Cubic x³ + 3x² +1 etc. etc.
4. 4 Biquadratic x⁴ -1

Classification of polynomials on the basis of no. of terms

Polynomial & Examples. Monomial – S₃Sx₃¹Yetc.

3

No. of terms

(i) 1

Binomial – (3 + 6x), (x – 5y) etc.

(ii) 2

(iii) 3

Trinomial- 2x² + 4x + 2 etc. etc.

• Constant polynomial: A polynomial containing one term only, consisting a constant term is called a constant polynomial the degree of non-zero constant polynomial is zero.
• Zero polynomial: A polynomial consisting of one term, namely zero only is called a zero polynomial. The degree of zero polynomial is not defined.
• Zeroes of a polynomial: Let p(x) be a polynomial. If p(a) =0, then we say that is a zero of the polynomial of p(x).
• Remark: Finding the zeroes of polynomial p(x) means solving the equation p(x)=0.
• Remainder theorem: Let f (x) be a polynomial of degree n > I and let a be any real

number. When f(x) is divided by (x – a) then the remainder is f (a)

• Factor theorem: Let f(x) be a polynomial of degree n > 1 and let a be any real number.

1. If f (a) = 0 then (x – a) is factor of f (x)
2. If (x – a) is factor of f (x)then f (a) = 0

• Factor: A polynomial p(x) is called factor of q(x) divides q(x) exactly.
• Factorization: To express a given polynomial as the product of polynomials each of degree less than that of the given polynomial such that no such a factor has a factor of lower degree, is called factorization.

CHAPTER – 1

NUMBER SYSTEMS

1. Rational Numbers
2. Irrational Numbers
3. Real Numbers and their Decimal Expansions
4. Operations on Real Numbers
5. Laws of Exponents for Real Numbers