Category: Maths

If a is a positive real number other than 1 and a^x = m, then x is called the logarithm of m to the base a, written as log_a m. In log_a m, m should be always positive.

(i) If m < 0, then log_a m will be imaginary and if m = 0, then log_a m will be meaningless.

(ii) log_a m exists only, if m, a > 0 and a ≠ 1.

Types of Logarithms

1. Natural or Napier Logarithms

The logarithms with base ‘e’ (e = 2.718) are called natural logarithms.

e.g., log_e x, log_e 25 etc.

2. Common or Brigg’s Logarithms

The logarithm with base ’10’ are called common logarithm.

e.g., log₁₀ x, log₁₀ 75 etc.

Note In a logarithmic expression when the base is not mentioned, it is taken as 10.

Characteristic and Mantissa of a Logarithm

The logarithm of positive real number ‘n’ consists of two parts.

1. The integral part is known as the characteristic. It is always an integer positive, negative or zero.
2. The decimal part is called as the mantissa. The mantissa is never negative and is always less than one.

< .strong>To Find the Characteristic

Case I. When the number is greater than 1.

The characteristic is one less than the number of digits in the left of decimal point in the given number.

e.g., 6.125 characteristic is O.

61.321 characteristic is 1.

725.132 characteristic is 2.

Case II. When the number is less than 1.

The characteristic is one more than the number of zero, between the decimal point and the fu-st significant digits of the number and it is negative.

e.g.. 0.7. characteristic is 1.

0.06712 characteristic ia 2.

0.00031 characteristic is 4.

Note In place of -1 or -2 etc.. we use 1 tone bar) and 2 (two bar) etc.

Properties of Logarithm

I. Characteristic of the logarithm of any number greater than I will be less than number of digits in the ‘integral part of the number’.

2. Characteristic of the logarithm of a number less than one negative and is one more than the number of zeros to the right of the decimal point in the number.

3. Since. a negative number can never be expressed as the power of 10, mantissa should always be kept positive. Hence, whenever characteristic ig negative, minus sign is placed above the characteristic and not to i. to show that the mantissa is always positive.

4. Mantissa of the logarithm of the number having same digits in the same order will be the same, irrespective of the position of the decimal point.

Anti-Logarithm

The positive number a is called the anti-logarithm of a number 6, if a Is anti-logarithm of b. then we write a = antilog b.

So, a = antilog b ⇔ log a = b

Important Results on Logarithm

Logarithmic Inequalities

(i) Let a is a real number such that a > 0, ≠ 1, then

(ii) Let a is a real number, then

(iii) Let a is a real number such that a > 0, ≠ 1, then (a)

Logic

Logic is the subject that deals with the method of reasoning. It provides us rules for determining the validity of a given argument in proving theorem.

Statement (Proposition)

A statement is an assertive sentence which is either true or false but not both a true statement is called valid statement. Otherwise it is called invalid statement. Statements are denoted by the small letters

i.e., p, q, r … etc.

Open and Compound Statement

A sentence which contains one or more variable such that when certain values are given to the variable it becomes a statement, is called an open statement.

If two or more simple statements are combined by the use of words such as ‘and’, ‘or’, ‘not’, ‘if’, ‘then’, ‘if and only if ‘, then the resulting statement is called a compound statement.

Truth Value and Truth Table

A statement can be either ‘true’ or ‘false’ which are called truth values of a .statement and it is represented by the symbols T and F, respectively.

A. truth table is a summary of truth values of the resulting statements for all possible assignment of values to the variables appearing in a compound statement.

Number of rows depends on their number of statements.

Truth Table for Two Statements (p, q)

Number of rows = 2² = 4

p	q
T	T
T	F
F	T
F	F

Elementary Operation of Logic

(i) Conjunction A compound sentence formed by two simple sentences p and q using connective ‘and’ is called the conjunction of p and q and it is represented by p ∧ q.

(ii) Disjunction A compound sentence formed by two simple sentences p and q using connectives ‘or’ is called the disjunction of p and q and it is represented by p ∨ q.

(iii) Negation A statement which is formed by changing the truth value of a given statement by using the word like ‘no’, ‘not’ is called negation of given statement. If p is a statement, then negation of p is denoted by ~ p.

(iv) Conditional Sentence (Implication) Two simple sentences p and q connected by the phase, if and then, is called conditional sentence of p and q arid it is denoted by p => q.

(v) Biconditional Sentence (Bi-implication) The two simple sentences connected by the phrase, ‘if and only if this is called biconditional sentences. It is denoted by the symbol ‘<=>’.

Table for Basic Logical Connections

Tautology and Contradiction

The compound statement which are true for every value of their components are called tautology.

The compound statements which are false for every value of their components are called contradiction (fallacy).

Truth Table

Quantifiers and Quantified Statements

In this statements, there are two important symbols are used.

(i) The symbol ‘∀’ stands for ‘all values of ‘.

This is known as universal quantifier.

(ii) The symbol ‘∃’ stands for ‘there exists’.

The symbol ∃ is known as existential quantifier.

Quantified Statement

An open sentence with a quantifier becomes a statement, called a quantified statement.

Negation of a Quantified Statement

(i) ~{∀ x ∈ A : p(x) is true} = {∃ x ∈ A such that (s.t.) ~ p(x) is true}

(ii) ~{∃x ∈ A : p(x) is true} = {∀ x ∈ A : ~ p(x) is true}

Laws of Algebra of Statements

(i) Idempotent Laws

(a) p ∨ p ≡ p

(b) p ∧ p ≡ p

(ii) Associative Laws

(a) (p ∨ q) ∨ r ≡ p ∨ (q ∨ r)

(b) (p ∧ q) ∧ r ≡ p ∧ (q ∧ r)

(iii) Commutative Laws

(a) p ∨ q ≡ q ∨ p

(b) p ∧ q ≡ q ∧ P

(iv) Distributive Laws

(a) p ∨ (q A r) ≡ (p ∨ q) ∧ (p ∨ r)

(b) p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)

(v) De Morgan’s Laws

(a) ~(p ∨ q) ≡ (~ p) ∧ (,_ q)

(b) ~(p ∧ q) ≡ (~ p) ∨ (~ q)

(vi) Identity Laws

(a) p ∧ F ≡ F

(b) p ∧ T ≡ p

(c) p ∨ T ≡ T

(d) p ∨ F ≡ p

(vii) Complement Laws

(a) p ∨ (~ p) ≡ T

(b) p ∧ (~ p) ≡ F

(c) ~ (~p) ≡ p

(d) ~ T ≡ F, ~ F ≡ T

Important Points to be Remembered

(i) The number of rows of table is depend on the number of statements.

(a) If p is false, then ~ p is true.

(b) If P is true, then ~ p is false.

(ii) (a) The converse of p => q is q => p.

(b) The inverse of p => q is ~ p => ~ q.

(iii) The contrapositive of p => q is ~ q => ~ p.

A statement which is neither a tautology nor a contradiction is a contingency.

Statistics is the Science of collection, organization, presentation, analysis and interpretation of the numerical data.

Useful Terms

1. Limit of the Class

The starting and end values of each class are called Lower and Upper limit.

2. Class Interval

The difference between upper and lower boundary of a class is called class interval or size of the class.

3. Primary and Secondary Data

The data collected by the investigator himself is known as the primary data, while the data collected by a person, other than the investigator is known as the secondary data.

4. Variable or Variate

A characteristics that varies in magnitude from observation to observation. e.g., weight, height, income, age, etc, are variables.

5. Frequency

The number of times an observation occurs in the given data, is called the frequency of the observation.

6. Discrete Frequency Distribution

A frequency distribution is called a discrete frequency distribution, if data are presented in such a way that exact measurements of the units are clearly shown.

7. Continuous Frequency Distribution

A frequency distribution in which data are arranged in classes groups which are not exactly measurable.

Cumulative Frequency Distribution

Suppose the frequencies are grouped frequencies or class frequencies. If however, the frequency of the first class is added to that of the second and this sum is added to that of the third and so on, then the frequencies, so obtained are known as cumulative frequencies (cf).

Graphical Representation of Frequency Distributions

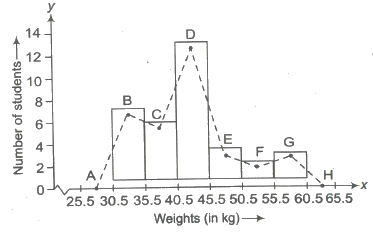
(i) Histogram To draw the histogram of a given continuous frequency distribution, we first mark off all the class intervals along X-axis on a suitable scale. On each of these class intervals on the horizontal axis, we erect (vertical) a rectangle whose height is proportional to the frequency of that particular class, so that the area of the rectangle is proportional to the frequency of the class.

If however the classes are of unequal width, then the height of the rectangles will be proportional to the ratio of the frequencies to the width of the classes.

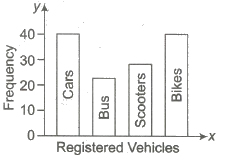
(ii) Bar Diagrams In bar diagrams, only the length of the bars are taken into consideration. To draw a bar diagram, we first mark equal lengths for the different classes on the axis, i.e., X-axis.

On each of these lengths on the horizontal axis, we erect (vertical) a rectangle whose heights is proportional to the frequency of the class.

(iii) Pie Diagrams Pie diagrams are used to represent a relative frequency distribution. A pie diagram consists of a circle divided into as many sectors as there are classes in a frequency distribution.

The area of each sector is proportional to the relative frequency of the class. Now, we make angles at the centre proportional to the relative frequencies.

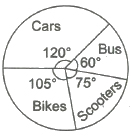
And in order to get the angles of the desired sectors, we divide 360° in the proportion of the various relative frequencies. That is,

Central angle = [Frequency x 360° / Total frequency]

(iv) Frequency Polygon To draw the frequency polygon of an ungrouped frequency distribution, we plot the points with abscissae as the variate values and the ordinate as the corresponding frequencies. These plotted points are joined by straight lines to obtain the frequency polygon.

(v) Cumulative Frequency Curve (Ogive) Ogive is the graphical representation of the cumulative frequency distribution. There are two methods of constructing an Ogive, viz (i) the ‘less than’ method (ii) the ‘more than’ method.

Measures of Central Tendency

Generally, average value of a distribution in the middle part of the distribution, such type of values are known as measures of central tendency.

The following are the five measures of central tendency

1. Arithmetic Mean

2. Geometric Mean

3. Harmonic Mean

4. Median

5. Mode

Arithmetic Mean

The arithmetic mean is the amount secured by dividing the sum of values of the items in a series by the number.

1. Arithmetic Mean for Unclassified Data

If n numbers, x₁, x₂, x₃,….., x_n, then their arithmetic mean

2. Arithmetic Mean for Frequency Distribution

Let f₁, f₂ , f_n be corresponding frequencies of x₁, x₂,…, x_n. Then,

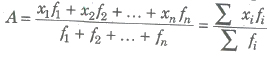
3. Arithmetic Mean for Classified Data

Class mark of the class interval a-b, then x = a + b / 2

For a classified data, we take the class marks x₁, x₂,…, x_n of the classes as variables, then arithmetic mean

Step Deviation Method

where, A₁ = assumed mean

u_i = x_i – A₁ / h

f_i = frequency

h = width of interval

4. Combined Mean

If x₁, x₂,…, x_r be r groups of observations, then arithmetic mean of the combined group x is called the combined mean of the observation

A = n₁ A₁ + n₂A₂ +….+ n_rA_r / n₁ + n₂ +…+ n_r

A_r = AM of collection x_r

n_r = total frequency of the collection x_r

5. Weighted Arithmetic Mean

If w be the weight of the variable x, then the weighted AM

A_w = Σ wx / Σ w

Shortcut Method

A_w = A_w‘ + Σ wd / Σ w, A_w‘ = assumed mean

Σ wd = sum of products of the deviations and weight

Properties of Arithmetic Mean

(i) Mean is dependent of change of origin and change of scale.

(ii) Algebraic sum of the deviations of a set of values from their arithmetic mean is zero.

(iii) The sum of the squares of the deviations of a set of values is minimum when taken about mean.

Geometric Mean

If x₁, x₂,…, x_n be n values of the variable, then

G = ⁿ√x₁, x₂,…, x_n

or G = antilog [log x₁ + log x₂ + … + log x_n / n]

For Frequency Distribution

Harmonic Mean (HM)

The harmonic mean of n items x₁, x₂,…, x_n is defined as

If their corresponding frequencies f₁, f₂,…, f_n respectively, then

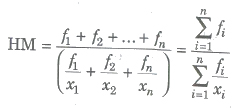
Median

The median of a distribution is the value of the middle variable when the variables are arranged in ascending or descending order.

Median (M_d) is an average of position of the numbers.

1. Median for Simple Distribution

Firstly, arrange the terms in ascending or descending order and then find the number of terms n.

(a) If n is odd, then (n + 1 / 2)th term is the median.

(b) If n is even, then there are two middle terms namely (n / 2)th and (n / 2 + 1)th terms. Hence,

Median = Mean of (n / 2)th and (n / 2 + 1)th terms.

2. Median for Unclassified Frequency Distribution

(i) First find N / 2, where N = Σ f_i.

(ii) Find the cumulative frequency of each value of the variable and take value of the variable which is equal to or just greater than N / 2

(iii) This value of the variable is the median.

3. Median for Classified Data (Median Class)

If in a continuous distribution, the total frequency be N, then the class whose cumulative frequency is either equal to N / 2 or is just greater than N / 2 is called median class.

For a continuous distribution, median

M_d = l + ((N / 2 – C) / f) * h

where, l = lower limit of the median class

f = frequency of the median class

N = total frequency = Σ f

C = cumulative frequency of the class just before the median class

h = length of the median class

Quartiles

The median divides the distribution in two equal parts. The distribution can similarly be divided in more equal parts (four, five, six etc.). Quartiles for a continuous distribution is given by

Q₁ = l + ((N / 4 – C) / f) * h

Where, N = total frequency

l = lower limit of the first quartile class

f = frequency of the first quartile class

C = the cumulative frequency corresponding to the class just before the first quartile class

h = the length of the first quartile class

Similarly, Q₃ = l + ((3N / 4 – C) / f) * h

where symbols have the same meaning as above only taking third quartile in place of first quartile.

Mode

The mode (M_o) of a distribution is the value at the point about which the items tend to be most heavily concentrated. It is generally the value of the variable which appears to occur most frequently in the distribution.

1. Mode for a Raw Data

Mode from the following numbers of a variable 70, 80, 90, 96, 70, 96, 96, 90 is 96 as 96 occurs maximum number of times.

2 For Classified Distribution

The class having the maximum frequency is called the modal class and the middle point of the modal class is called the crude mode.

The class just before the modal class is called pre-modal class and the class after the modal class is called the post-modal class.

Mode for Classified Data (Continuous Distribution)

M_o = l + (f₀ – f₁ / 2 f₀ – f₁ – f₂) x h

Where, 1 = lower limit of the modal class

f₀ = frequency of the modal class

f₁ = frequency of the pre-modal class

f₂ = frequency of the post-modal class

h = length of the class interval

Relation between Mean, Median and Mode

(i) Mean — Mode = 3 (Mean — Median)

(ii) Mode = 3 Median — 2 Mean

Symmetrical and Skew distribution

A distribution is symmetric, if the same number of frequencies is found to be distributed at the same linear teance on either side of the mode. The frequency curve is bell shaped and A = M_d = M_o

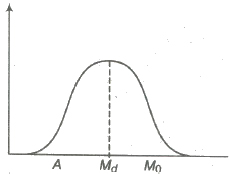
In anti-symmetric or skew distribution, the variation does not have symmetry.

(i) If the frequencies increases sharply at beginning and decreases slowly after modal value, then it is called positive skewness and A > M_d > M_o.

(ii) If the frequencies increases slowly and decreases sharply after modal value, the skewness is said to be negative and A < M_d < M_o.

Measure of Dispersion

The degree to which numerical data tend to spread about an average value is called the dispersion of the data. The four measure of dispersion are

1. Range
2. Mean deviation
3. Standard deviation
4. Square Deviation

Range

The difference between the highest and the lowest element of a data called its range.

i.e., Range = X_{max – Xmin}

∴ The coefficient of range = X_{max – Xmin / Xmax + Xmin}

It is widely used in statistical series relating to quality control in production.

(i) Inter quartile range = Q₃ — Q₁

(ii) Semi-inter quartile range (Quartile deviation)

∴ Q D = Q₃ — Q₁ / 2

and coefficient of quartile deviation = Q₃ — Q₁ / Q₃ + Q₁

(iii) QD = 2 / 3 SD

Mean Deviation (MD)

The arithmetic mean of the absolute deviations of the values of the variable from a measure of their Average (mean, median, mode) is called Mean Deviation (MD). It is denoted by δ.

(i) For simple (discrete) distribution

δ = Σ |x – z| / n

where, n = number of terms, z = A or M_d or M_o

(ii) For unclassified frequency distribution

δ = Σ f |x – z| / Σ f

(iii) For classified distribution

δ = Σ f |x – z| / Σ f

Here, x is for class mark of the interval.

(iv) MD = 4 / 5 SD

(v) Average (Mean or Median or Mode) = Mean deviation from the average / Average

Note The mean deviation is the least when measured from the median.

Coefficient of Mean Deviation

It is the ratio of MD and the mean from which the deviation is measured. Thus, the coefficient of MD

= δ A / A or δ M _d / M _d or δ M _o / M _o

Standard Deviation (σ)

Standard deviation is the square root of the arithmetic mean of the squares of deviations of the terms from their AM and it is denoted by σ.

The square of standard deviation is called the variance and it is denoted by the symbol σ².

(i) For simple (discrete) distribution

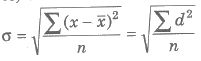
(ii) For frequency distribution

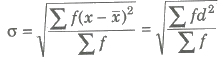
(iii) For classified data

Here, x is class mark of the interval.

Shortcut Method for SD σ =

where, d = x — A’ and A’ = assumed mean

Standard Deviation of the Combined Series

If n₁, n₂ are the sizes, X₁, X₂ are the means and σ₁, σ₂ are the standard deviation of the series, then the standard deviation of the combined series is

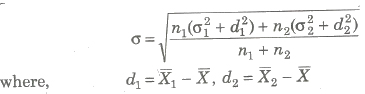
Effects of Average and Dispersion on Change of origin and Scale

	Change of origin	Change of scale
Mean	Dependent	Dependent
Median	Not dependent	Dependent
Mode	Not dependent	Dependent
Standard Deviation	Not dependent	Dependent
Variance	Not dependent	Dependent

Important Points to be Remembered

(i) The ratio of SD (σ) and the AM (x) is called the coefficient of standard deviation (σ / x).

(ii) The percentage form of coefficient of SD i.e., (σ / x) * 100 is called coefficient of variation.

(iii) The distribution for which the coefficient of variation is less is called more consistent.

(iv) Standard deviation of first n natural numbers is √n² – 1 / 12

(v) Standard deviation is independent of change of origin, but it is depend on change of scale.

Root Mean Square Deviation (RMS)

The square root of the AM of squares of the deviations from an assumed mean is called the root mean square deviation. Thus,

(i) For simple (discrete) distribution

S = √Σ (x – A’)² / n, A’ = assumed mean

(ii) For frequency distribution

S = √Σ f (x – A’)² / Σ f

if A’ — A (mean), then S = σ

Important Points to be Remembered

(i) The RMS deviation is the least when measured from AM.

(ii) The sum of the squares of the deviation of the values of the variables is the least when measured from AM.

(iii) σ² + A² = Σ fx² / Σ f

(iv) For discrete distribution f =1, thus σ² + A² = Σ x² / n.

(v) The mean deviation about the mean is less than or equal to the SD. i.e., MD ≤ σ

Correlation

The tendency of simultaneous variation between two variables is called correlation or covariance. It denotes the degree of inter-dependence between variables.

1. Perfect Correlation

If the two variables vary in such a manner that their ratio is always constant, then the correlation is said to be perfect.

2. Positive or Direct Correlation

If an increase or decrease in one variable corresponds to an increase or decrease in the other, then the correlation is said to the negative.

3. Negative or Indirect Correlation

If an increase of decrease in one variable corresponds to a decrease or increase in the other, then correlation is said to be negative.

Covariance

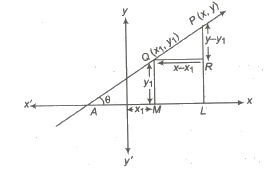
Let (x_i, y_i), i = 1, 2, 3, , n be a bivariate distribution where x₁, x₂,…, x_n are the values of variable x and y₁, y₂,…, y_n those as y, then the cov (x, y) is given by

where, x and y are mean of variables x and y.

Karl Pearson’s Coefficient of Correlation

The correlation coefficient r(x, y) between the variable x and y is given

r(x, y) = cov(x, y) / √var (x) var (y) or cov (x, y) / σ_x σ_y

If (x_i, y_i), i = 1, 2, … , n is the bivariate distribution, then

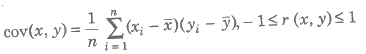
Properties of Correlation

(i) – 1 ≤ r ≤ 1

(ii) If r = 1, the coefficient of correlation is perfectly positive.

(iii) If r = – 1, the correlation is perfectly negative.

(iv) The coefficient of correlation is independent of the change in origin and scale.

(v) If -1 < r < 1, it indicates the degree of linear relationship between x and y, whereas its sign tells about the direction of relationship.

(vi) If x and y are two independent variables, r = 0

(vii) If r = 0, x and y are said to be uncorrelated. It does not imply that the two variates are independent.

(viii) If x and y are random variables and a, b, c and d are any numbers such that a ≠ 0, c ≠ 0, then

r(ax + b, cy + d) = |ac| / ac r(x, y)

(ix) Rank Correlation (Spearman’s) Let d be the difference between paired ranks and n be the number of items ranked. The coefficient of rank correlation is given by

ρ = 1 – Σd² / n(n² – 1)

(a) The rank correlation coefficient lies between – 1 and 1.

(b) If two variables are correlated, then points in the scatter diagram generally cluster around a curve which we call the curve of regression.

(x) Probable Error and Standard Error If r is the correlation coefficient in a sample of n pairs of observations, then it standard error is given by

1 – r² / √n

And the probable error of correlation coefficient is given by (0.6745) (1 – r² / √n).

Regression

The term regression means stepping back towards the average.

Lines of Regression

The line of regression is the line which gives the best estimate to the value of one variable for any specific value of the other variable. Therefore, the line of regression is the line of best fit and is obtained by the principle of least squares.

Regression Analysis

(i) Line of regression of y on x,

y — y = r σ_y / σ_x (x – x)

(ii) Line of regression of x and y,

x – x = r σ_x / σ_y (y — y)

(iii) Regression coefficient of y on x and x on y is denoted by

b_yx = r σ_y / σ_x, b_yx = cov (x, y) / σ²_x and b_yx = r σ_x / σ_y, b_xy = cov (x, y) / σ²_y

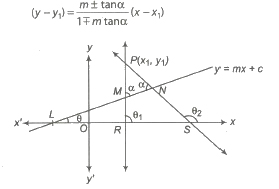
(iv) Angle between two regression lines is given by

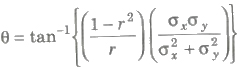
(a) If r = 0, θ = π / 2 , i.e., two regression lines are perpendicular to each other.

(b) If r = 1 or — 1, θ = 0, so the regression lines coincide.

Properties of the Regression Coefficients

(i) Both regression coefficients and r have the same sign.

(ii) Coefficient of correlation is the geometric mean between the regression coefficients.

(iii) 0 < |b_xy b_yx| le; 1, if r ≠ 0

i.e., if |b_xy|> 1, then | b_yx| < 1

(iv) Regression coefficients are independent of the change of origin but not of scale.

(v) If two regression coefficient have different sign, then r = 0.

(vi) Arithmetic mean of the regression coefficients is greater than the correlation coefficient.

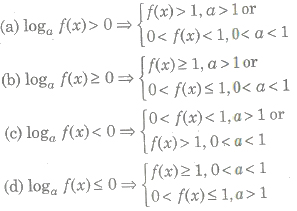
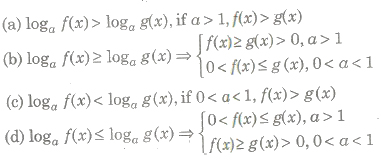
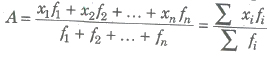
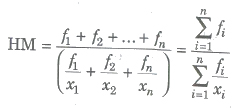
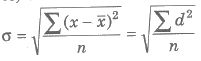
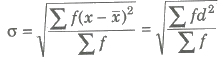
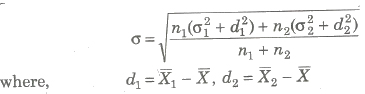
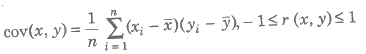
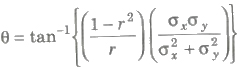
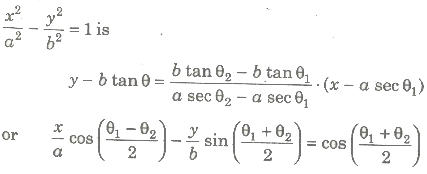
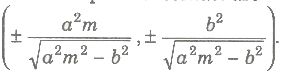
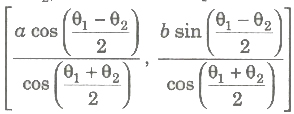
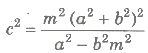
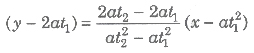
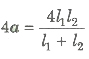
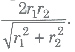
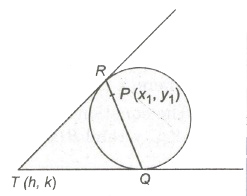
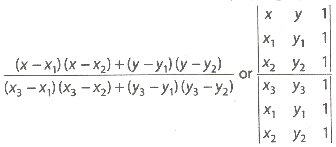
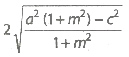
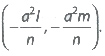
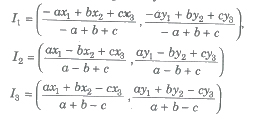
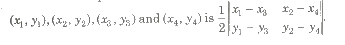
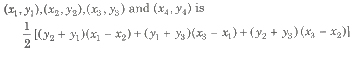
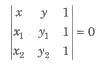
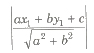
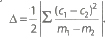A hyperbola is the locus of a point in a plane which moves in the plane in such a way that the ratio of its distance from a fixed point in the same plane to its distance from a fixed line is always constant, which is always greater than unity.

The fixed point is called the focus and the fixed line is directrix and the ratio is the eccentricity.

Transverse and Conjugate Axes

The line through the foci of the hyperbola is called its transverse axis.

The line through the centre and perpendicular to the transverse axis of the hyperbola is called its conjugate axis.

1. Centre O(0, 0)
2. Foci are S(ae,0),S₁(-ae, 0)
3. Vertices A(a, 0), A₁(-a, 0)
4. Directrices / : x = a/e, l’ : x = -a/e
5. Length of latusrectum LL₁ = L’L’₁ = 2b²/a
6. Length of transverse axis 2a.
7. Length of conjugate axis 2b.
8. Eccentricityor b² = a²(e² – 1)
9. Distance between foci =2ae
10. Distance between directrices = 2a/e

Conjugate Hyperbola

1. (i) Centre O(0, 0)
2. (ii) Foci are S (0, be), S₁(0, — be)
3. (iii) Vertices A(0, b) , A₁(0, — b)
4. (iv) Directrices
   l:y = b/e, l’ : y = —b/e
5. (v) Length of latusrectum
   LL₁ = L’ L’₁ = 2a₂/b
6. (vi) Length of transverse axis 2b.
7. (vii) Length of conjugate axis 2a.
8. (viii) Eccentricity
   
9. (ix) Distance between foci = 2be
10. (x) Distance between directrices = 2b/e

Focal Distance of a Point

The distance of a point on the hyperbola from the focus is called it focal distance. The difference of the focal distance of any point on a, hyperbola is constant and is equal to the length of transverse axis the hyperbola i.e.,

S₁P — SP = 2a

where, S and S₁ are the foci and P is any point or P the hyperbola.

Equation of Hyperbola in Different Form

1 If the centre of the hyperbola is (h, k) and the directions of the axes are parallel to the coordinate axes, then the equation of the hyperbola, whose transverse and conjugate axes are 2a and 2b is

2. If a point P(x, y) moves in the plane of two perpendicular straight lines a₁x + b₁y + c₁ = 0 and b₁x – a₁y + c₂ = 0 in such a way that

Then, the locus of P is hyperbola whose transverse axis lies along b₁x – a₁y + c₂ = 0 and conjugate axis along the line a₁x + b₁y + c₁ = 0. The length of transverse and conjugate axes are 2a and 2b, respectively.

Parametric Equations

(i) Parametric equations of the hyperbola

x = a sec θ, y = b tan θ
or x = a cosh θ, y = b sinhθ

(ii) The equationsare also the parametric equations of the hyperbola.

Equation of Chord

(i) Equations of chord joining two points P(a sec θ₁, b tan θ₁,) and Q(a sec θ₂, b tan θ₂) on the hyperbola

(ii) Equations of chord of contact of tangents drawn from a point (x₁, y₁) to the hyperbola

(iii) The equation of the chord of the hyperbolabisected at point (x₁, y₁) is given by

Equation of Tangent Hyperbola

(i) Point Form The equation of the tangent to the hyperbola 

(ii) Parametric Form The equation of the tangent to the hyperbola

(iii) Slope Form The equation of the tangents of slope m to the hyperbola

The coordinates of the point of contact are

(iv) The tangent at the points P(a sec θ₁ , b tan θ₁) and Q (a sec θ₂, b tan θ₂) intersect at the point

(v) Two tangents drawn from P are real and distinct, coincident or imaginary according as the roots of the equation m²(h² – a²) – 2khm + k² + b² = 0. are real and distinct, coincident or imaginary.

(vi) The line y = mx + c touches the hyperbola, if c² = a²m² – b² the point of contacts

Normal Equation of Hyperbola

(i) Point Form The equation of the normal to the hyperbola

(ii) Parametric Form The equation of the normal at (a sec θ, b tan θ) to the hyperbola
is ax cos θ + by cot θ = a² + b².

(iii) Slope Form The equations of the normal of slope m to the hyperbolaare given by

The coordinates of the point of contact are

(iv) The line y = mx + c will be normal to the hyperbolaif,

(v) Maximum four normals can be drawn from a point (x₁, y₁) to the hyperbola

Conormal Points

Points on the hyperbola, the normals at which passes through a given point are called conormal points.

1. The sum of the eccentric angles of conormal points is an odd ion multiple of π.
2. If θ₁ , θ₂ , θ₃ and θ₄ are eccentric angles of four points on the hyperbola , then normal at which they are concurrent, then
   (a) ∑cos( θ₁ + θ₂) = 0
   (b) ∑sin( θ₁ + θ₂) = 0
3. If θ₁ , θ₂ and θ₃ are the eccentric angles of three points on the hyperbola, such that sin(θ₁ + θ₂) + sin(θ₂ + θ₃) + sin(θ₃ + θ₁) = 0. Then, the normals at these points are concurrent.
4. If the normals at four points P(x₁, y₁), Q(x₂, y₂), R(x₃ , y₃) and S(X₄, y₄) on the hyperbola are concurrent, then

Conjugate Points and Conjugate Lines

1. Two points are said to be conjugate points with respect to a hyperbola, if each lies on the polar of the other.
2. Two lines are said to be conjugate lines with respect to a hyperbola , if each passes through the pole of the other.

Diameter and Conjugate Diameter

1. Diameter The locus of the mid-points of a system of parallel chords of a hyperbola is called a diameter.>
   The equation of the diameter bisecting a system of parallel chord of slope m to the hyperbola is
   
2. Conjugate Diameter The diameters of a hyperbola are sal to be conjugate diameter, if each bisect the chords parallel to th other.
   The diameters y = m₁x and y = m₂x are conjugate, if m₁ m₂ = b²/a².
3. In a pair of conjugate diameters of a hyperbola, only one mee the hyperbola in real points.

Asymptote

An asymptote to a curve is a straight line, at a finite distance from the origin, to which the tangent to a curve tends as the point of contact goes to infinity.

1. The equation of two asymptotes of the hyperbola are 
2. The combined equation of the asymptotes to the hyperbola
3. When b = a, i.e., the asymptotes of rectangular hyperbola x² – y² = a² are y = ± x which are at right angle.
4. A hyperbola and its conjugate hyperbola have the same asymptotes.
5. The equation of the pair of asymptotes differ the hyperbola and the conjugate hyperbola by the same constant only i.e., Hyperbola — Asymptotes = Asymptotes — Conjugate hyperbola
6. The asymptotes pass through the centre of the hyperbola.
7. The bisectors of angle between the asymptotes are the coordinate axes.
8. The angle between the asymptotes of is 2 tan^-1(b/a) or 2 sec^-1(e).

Director Circle

The locus of the point of intersection of the tangents to the hyperbolo, which are perpendicular to each other, is called a director circle. The equation of director circle is x² + y² = a² – b².

Rectangular Hyperbola

A hyperbola whose asymptotes include a right angle is said to I rectangular hyperbola or we can say that, if the lengths of transver: and conjugate axes of any hyperbola be equal, then it is said to be rectangular hyperbola.

i.e., In a hyperbola. if b = a, then it said to be rectangular hyperbola.

The eccentricity of a rectangular hyperbola is always √2.

Rectangular Hyperbola of the Form x² – y² = a²

1. Asymptotes are perpendicular lines i.e., x ± y = 0
2. Eccentricity e = √2.
3. Centre (0, 0)
4. Foci (± -√2 a, 0)
5. Vertices A(a, 0) and A1 (—a, 0)
6. Directrices x = + a/√2
7. Latusrectum = 2a
8. Parametric form x = a sec θ, y = a tan θ
9. Equation of tangent, x sec θ – y tan θ = a

Rectangular Hyperbola of the Form xy = c²

1. Asymptotes are perpendicular lines i.e., x = 0 and y = 0
2. Eccentricity e = √2
3. Centre (0, 0)
4. Foci S(√2c, √2c), S₁(-√2c, -√2c)
5. Vertices A(c, c), A1(— c,— c)
6. Directrices x + y = ±√2c
7. Latusrectum = 2√2c
8. Parametric form x = ct, y = c/t

Tangent Equation of Rectangular Hyperbola xy = c²

1. Point Form The equation of tangent at (x₁, y₁) to the rectangular hyperbola is xy₁ + yx₁= 2c² or (x/x₁ + y/y₁) = 2.
2. Parametric Form The equation of tangent at (ct, c/t) to the hyperbola is( x/t + yt) = 2c.
3. Tangent at P(ct₁, c/t₁) and Q (ct₂, c/t₂) to the rectangular hyperbola intersect a 
4. The equation of the chord of contact of tangents drawn from a point (x₁, y₁) to the rectangular hyperbola is xy₁ + yx₁ = 2c².

Normal Equation of Rectangular Hyperbola xy = c²

1. Point Form The equation of the normal at (x₁, y₁) to the rectangular hyperbola is xx₁ – yy₁ = x₁² – y₁².
2. Parametric Form The equation of the normal at ( ct, c/t)to the rectangular hyperbola xy = c² is xt³ — yt — ct⁴ + c = O.
3. The equation of the normal at( ct, c/t)is a fourth degree equation t in t. So, in general four normals can be drawn from a point to the hyperbola xy = c².

Important Points to be Remembered

1. The point (x1, y1) lies outside, on or inside the hyperbolaaccording as
2. The combined equation of the pairs of tangent drawn from a point P(x₁, y₁) lying outside the hyperbola
3. The equation of the chord of the hyperbola xy = c² whose mid-point is (x₁, y₁) is
   xy₁ + yx₁ = 2x₁y₁
   or t = S₁
4. Equation of the chord joining t₁, t₂ on xy = t² is
   x + yt₁t₂ = c(t₁ + t₂)
5. Eccentricity of the rectangular hyperbola is √2 and the angle between asymptotes is 90°.
6. If a triangle is inscribed in a rectangular hyperbola, then its orthocentre lies on the hyperbola.
7. Any straight line parallel to an asymptotes of a hyperbola intersects the

Ellipse is the locus of a point in a plane which moves in such a way that the ratio of the distance from a fixed point (focus) in the same plane to its distance from a fixed straight line (directrix) is always constant, which is always less than unity.

Major and Minor Axes

The line segment through the foci of the ellipse with its end points on the ellipse, is called its major axis.

The line segment through the centre and perpendicular to the major axis with its end points on the ellipse, is called its minor axis.

Horizontal Ellipse i.e., x² / a² + y² / b² = 1, 0 < b < a

If the coefficient of x² has the larger denominator, then its major axis lies along the x-axis, then it is said to be horizontal ellipse.

(i) Vertices A( a, 0), A_l (- a, 0)

(ii) Centre (0, 0)

(iii) Major axis, AA_l = 2a; Minor axis, BB_l = 2b

(iv) Foci are S(ae, 0) and S_l(-ae, 0)

(v) Directrices are l : x = a / e, l’ ; x = – a / e

(vi) Latusrectum, LL_l = L’ L_l‘ = 2b² / a

(vii) Eccentricity, e = √1 – b² / a² < 1

(viii) Focal distances are SP and S_lP i.e., a – ex and a + ex. Also, SP + S_lP = 2a = major axis.

(ix) Distance between foci = 2ae

(x) Distance between directrices = 2a / e

Vertical Ellipse i.e., x² / a² + y² / b² = 1, 0 < a < b

If the coefficient of x² has the smaller denominator, then its major axis lies along the y-axis, then it is said to be vertical ellipse.

(i) Vertices B(O, b), B_l(0,- b)

(ii) Centre O(0,0)

(iii) Major axis BB_l = 2b; Minor axis AA_l = 2a

(iv) Foci are S(0, ae) and S_l(0, – ae)

(v) Directrices are l : y = b / e ; l’ : y = – b / e

(vi) Latusrectum LL_l = L’L_l‘ = 2a² / b

(vii) Eccentricity e = √1 – a² / b² < 1

(viii) Focal distances are SP and S_lP.

i.e., b – ex and b + ex axis.

Also, SP + S_lP = 2b = major axis.

(ix) Distance between foci = 2be

(x) Distance between directrices = 2b / e

Ordinate and Double Ordinate

Let P be any point on the ellipse and PN be perpendicular to the major axis AA’, such that PN produced meets the ellipse at P’. Then, PN is called the ordinate of P and PNP’ is the double ordinate of P .

Special Form of Ellipse

If centre of the ellipse is (h, k) and the direction of the axes are parallel to the coordinate axes, then its equation is (x – h)² / a² + (y – k)² / b² = 1

Position of a Point with Respect to an Ellipse

The point (x₁, y_{1) lies outside, on or inside the ellipse x² / a² + y² / b² = 1 according as x²1 / a² + y²1 / b² – 1 > 0, = or < 0.}

Auxiliary Circle

the ellipse x² / a² + y² / b² = 1, becomes the ellipse x² + y² = a², if b = a. This is called auxiliary circle of the ellipse. i. e. , the circle described on the major axis of an ellipse as diameter is called auxiliary circle.

Director Circle

The locus of the point of intersection of perpendicular tangents to an ellipse is a director circle. If equation of an ellipse is x² / a² + y² / b² = 1, then equation of director circle is x²+ y² = a² + b².

Eccentric Angle of a Point

Let P be any point on the ellipse x² / a² + y² / b² = 1. Draw PM perpendicular a b from P on the major axis of the ellipse and produce MP to the auxiliary circle in Q. Join CQ. The ∠ ACQ = φ is called the eccentric angle of the point P on the ellipse.

Parametric Equation

The equation x = a cos φ, y = b sin φ, taken together are called the parametric equations of the ellipse x² / a² + y² / b² = 1 , where φ is any parameter.

Equation of Chord

Let P(a cos θ, b sin θ) and Q(a cos φ, b sin φ) be any two points of the ellipse x² / a² + y²/ b² = 1.

(i) The equation of the chord joining these points will be

(y – b sin θ) = b sin φ – b sin θ / a cos φ – a sin θ (x – a cos θ)

or x / a cos ( θ + φ / 2) + y / b sin ( θ + φ / 2) = cos ( θ – φ / 2)

(ii) The equation of the chord of contact of tangents drawn from an point (x₁, y₁) to the ellipse

x² / a² + y² / b² = 1 is xx₁ / a² + yy₁ / b² = 1.

(iii) The equation of the chord of the ellipse x² / a² + y² / b² = 1 bisected at the point (x₁, y₁) is given by

xx₁ / a² + yy₁ / b² – 1 = x²₁ / a² + y²₁ / b² – 1

or T = S₁

Equation of Tangent

(i) Point Form The equation of the tangent to the ellipse x² / a² + y² / b² = 1 at the point (x₁, y₁) is xx₁ / a² + yy₁ / b² = 1.

(ii) Parametric Form The equation of the tangent to the ellipse at the point (a cos θ, b sin θ) is x / a cos θ + y / b sin θ = 1.

(iii) Slope Form The equation of the tangent of slope m to the ellipse x² / a² + y² / b² = 1 are y = mx ± √a²m² + b² and the coordinates of the point of contact are

(iv) Point of Intersection of Two Tangents The equation of the tangents to the ellipse at points P(a cosθ₁, b sinθ₁) and Q (a cos θ₂, b sinθ₂) are

x / a cos θ₁ + y / b sin θ₁ = 1 and x / a cos θ₂ + y / b sin θ₂ = 1

and these two intersect at the point

Equation of Normal

(i) Point Form The equation of the normal at (x₁, y₁) to the ellipse x² / a² + y² / b² = 1 is

a²x / x₁ + b²y / y₁ = a² – b²

(ii) Parametric Form The equation of the normal to the ellipse x² / a² + y² / b² = 1 at (a cos θ, b sin θ) is

ax sec θ – by cosec θ = a² – b²

(iii) Slope Form The equation of the normal of slope m to the ellipse x² / a² + y² / b² = 1 are given by y = mx – m (a² – b²) / √a² + b²m²

and the coordinates of the point of contact are

(iv) Point of Intersection of Two Normals Point of intersection of the normal at points (a cos θ₁, b sin θ₁) and (a cos θ₂, b sin θ₂) are given by

(v) If the line y = mx + c is a normal to the ellipse x² / a² + y² / b² = 1, then

c² = m²(a² – b²)² / a² + b²m²

Conormal Points

The points on the ellipse, the normals at which the ellipse passes through a given point are called conormal points.

Here, P, Q, R and S are the conormal points.

(i) The sum of the eccentric angles of the conormal points on the ellipse, x² / a² + y² / b² = 1 is an odd multiple of π.

(ii) If θ₁, θ₂, θ₃ and θ₄ are eccentric angles of four points on the ellipse, the normals at which are concurrent, then

(a) Σ cos (θ₁ + θ₂) = 0

(b) Σ sin (θ₁ + θ₂) = 0

(iii) If θ₁, θ₂ and θ₃ are the eccentric angles of three points on the ellipse x² / a² + y² / b²= 1, such that

sin (θ₁ + θ₂) + sin (θ₂ + θ₃) + sin (θ₃ + θ₁) = 0,

then the normal at these points are concurrent.

(iv) If the normal at four points P(x₁, y₁) , Q(x₂, y₂), R(x₃, y₃) and S(x₄, y₄) on the ellipse x² / a² + y² / b² = 1, are concurrent, then

(x₁ + x₂ + x₃ + x₄) (1 / x₁ + 1 / x₂ + 1 / x₃ + 1 / x₄) = 4

Diameter and Conjugate Diameter

The locus of the mid-point of a system of parallel chords of an ellipse is called a diameter, whose equation of diameter is

y = – (b² / a²m) x

Two diameters of an ellipse are said to be conjugate diameters, if each bisects the chords parallel to the other.

Properties of Conjugate Diameters

(i) The eccentric angles of the ends of a pair of conjugate diameters of an ellipse differ by a right angle.

(ii) The sum of the squares of any two conjugate semi-diameters of an ellipse is constant and equal to the sum of the squares of the semi-axis of the ellipse i. e., CP² + CD² = a² + b².

(iii) If CP, CQ are two conjugate semi-diameters of an ellipse x² / a² + y² / b² = 1 and S, S₁ be two foci of an ellipse, then

SP * S₁P = CQ²

(iv) The tangent at the ends of a pair of conjugate diameters of an ellipse form a parallelogram.

(v) The area of the parallelogram formed by the tangents at the ends of conjugate diameters of an ellipse is constant and is equal to the product of the axis.

Important Points

1. The point P(x₁ y₁) lies outside, on or inside the ellipse x² / a² + y² / b² = 1 according as x²₁ / a² + y²₁ / b² – 1 > 0, or < 0.

2. The line y = mx + c touches the ellipse

x² / a² + y² / b² = 1, if c² = a²m² + b²

3. The combined equation of the pair of tangents drawn from a point (x₁ y₁) to the ellipse x² / a² + y² / b² = 1 is

(x² / a² + y² / b² – 1) (x²₁ / a² + y²₁ / b² – 1) = (xx₁ / a² + yy₁ / b² – 1)²

i.e, SS₁ = T²

4. The tangent and normal at any point of an ellipse bisect the external and internal angles between the focal radii to the point.

5. If SM and S’ M’ are perpendiculars from the foci upon the tangent at any point of the ellipse, then SM x S’ M’ = b² and M, M’ lie on the auxiliary circle.

6. If the tangent at any point P on the ellipse x² / a² + y² / b² = 1 meets the major axis in T and minor axis in T’, then CN * CT = a² ,CN’ * Ct’ = p², where N and N’ are the foot of the perpendiculars from P on the respective axis.

7. The common chords of an ellipse and a circle are equally inclined to the axes of the ellipse.

8. The four normals can be drawn from a point on an ellipse.

9. Polar of the point (x₁ y₁) with respect to the ellipse x² / a² + y² / b² = 1 is xx₁ / a² + yy₁/ b² = 1.

Here, point (x₁ y₁) is the pole of xx₁ / a² + yy₁ / b² = 1.

10. The pole of the line lx + my + n = 0 with respect to ellipse x² / a² + y² / b² = 1 is

p(-a²l / n, -b²m / n).

11. Two tangents can be drawn from a point P to an ellipse. These tangents are real and distinct or coincident or imaginary according as the given point lies outside, on or inside the ellipse.

12. Tangents at the extremities of latusrectum of an ellipse intersect on the corresponding direction.

13. Locus of mid-point of focal chords of an ellipse x² / a² + y² / b² = 1 is

x² / a² + y² / b² = ex / a².

14. Point of intersection of the tangents at two points on the ellipse x² / a² + y² / b² = 1, whose eccentric angles differ by a right angles lies on the ellipse x² / a² + y² / b² = 2.

15. Locus of mid – point of normal chords of an ellipse x² / a² + y² / b² = 1 is

(x² / a² + y² / b²)² (a⁶ / x² + b⁶ / y²) = (a² – b²)².

16. Eccentric angles of the extremities of latusrectum of an ellipse x² / a² + y² / b² = 1 are

tan^-1 ( ± b / ae).

17. The straight lines y = m₁x and y =m₂x are conjugate diameters of an ellipse x² / a² + y² / b² = 1, if m₁m₂ = – b² / a².

18. The normal at point P on an ellipse with foci S, S₁ is the internal bisector of ∠ SPS₁.

Conic Section

A conic is the locus of a point whose distance from a fixed point bears a constant ratio to its distance from a fixed line. The fixed point is the focus S and the fixed line is directrix l.

The constant ratio is called the eccentricity denoted by e.

1. If 0 < e < 1, conic is an ellipse.
2. e = 1, conic is a parabola.
3. e > 1, conic is a hyperbola.
4. If fixed point of curve is (x₁, y₁) and fixed line is ax + by + c = then equation of the conic is
   (a² + b²) [(x — x₁)² + (y — y₁)²] = e²(ax + by + c)²

General Equation of Conic

A second degree equation ax² + 2hxy + by² + 2gx + 2fy + c= 0 represents

1. Pair of straight lines, if
2. Circle, if a = b, h = 0
3. Parabola, if h² = ab and Δ ≠ 0
4. Ellipse, if h² < ab and Δ ≠ 0
5. Hyperbola, if h² > ab and Δ ≠ 0
6. Rectangular hyperbola, if a + b = 0 and Δ ≠ 0

Parabola

A parabola is the locus of a point which moves in a plane such that its distance from a fixed point in the plane is always equal to its distance from a fixed straight line in the same plane.

If focus of a parabola is S(x₁, y₁) and equation of the directrix is ax + by + c = 0, then the equation of the parabola is

(a² + b²)[(x – x₁)² + (y – y₁)²] = (ax + by + c)²

Definitions Related to Parabola

1. Vertex The intersection point of parabola and axis.
2. Centre The point which bisects every chord of the conic passing through it.
3. Focal Chord Any chord passing through the focus.
4. Double Ordinate A chord perpendicular to the axis of a conic.
5. Latusrectum A double ordinate passing through the focus of the parabola.
6. Focal Distance The distance of a point P(x, y) from the focus S is called the focal distance of the point P.

Other Forms of a Parabola

If the vertex of the parabola is at a point A(h , k) and its latusrectum is of length 4a, then its equation is

1. (y – k)² = 4a (x – h), its axis is parallel to OX i. e. , parabola open rightward.
2. (y – k)² = – 4a (x – h), its axis is parallel to OX’ i. e., parabola open leftward.
3. (x – h)² = – 4a (y – k), its axis is parallel to OY i.e., parabola open upward.
4. (x – h)² = – 4a (y – k), its axis is parallel to OY ‘ i.e., parabola open downward. –
5. The general equation of a parabola whose axis is parallel to X – axis is x = ay² + by + c and the general equation of a parabola whose axis is parallel to Y-axis is y = ax² + bx + c.

Position of a Point

The point (x₁, y₁) lies outside, on or inside the parabola y² = 4ax according as y₁² — 4ax₁>, =, < 0.

Chord

Joining any two points on a curve is called chord.

(i) Parametric Equation of a Chord Let P(at₁² , 2at₁) and Q (at₂², 2at₂) be any two points on the parabola y₁ = 4ax, then the equation of the chord is

or y (t₁ + t₁) = 2x + 2at₁t₂

(ii) Let P(at² , 2at) be the one end of a focal chord PQ of the parabola y² = 4ax, then the coordinates of the other end Q are

(a/t², -2a/t)

(iii) If  l₁ and l₂ are the length of the focal segments, then length of the latusrectum = 2 (harmonic mean of focal segment)

i.e.,  

(iv) For a chord joining points P(at₁² , 2at₁) and Q(at₂² , 2at₂) and passing through focus, then t₁t₂ = 1.
(v) Length of the focal chord having t₁ and t₂ as end points is a (t₁ — t₁)².
(vi) Chord of contact drawn from a point (x₁, y₁) to the parabola y² = 4ax is yy₁, = 2a (x + x₁)

(vii) Equation of the chord of the parabola y² = 4ax, which is bisected at (x₁ , y₁) is given by

T = S₁
i.e. , yy₁ — 2a (x + x₁) = y₁² – 4ax

Equation of Tangent

A line which touch only one point of a parabola.

(i) Point Form The equation of the tangent to the parabola y² = 4ax at a point (x₁, y₁) is given by yy₁ = 2a (x + x₁)

(ii) Slope Form

(a) The equation of the tangent of slope m to the parabola y² = 4ax is

y = (mx + a/m)

(b) The equation of the tangent of slope m to the parabola (y – k)² = 4a (x – h) is given by

(y – k)² = m (x — h) + a/m

The coordinates of the point of contact are

(iii) Parametric Form The equation of the tangent to the parabola y² = 4ax at a point (at², 2at) is yt = x + at²

(iv) The line y = mx + c touches a parabola, if c = a/m and the point of contact is

(v) Point of Intersection of Two Tangents Let two tangents at P(at₁² , 2at₁) and Q(at₂², 2at₂) intersect at R. Then, their point of intersection is R[at₁t₂, a(t₁ + t₂)] i.e., (GM of abscissa, AM of ordinate).

(vi) The straight line lx + my + n = 0 touches y² = 4ax, if nl = am² and x cos α + y sin α = p touches y² = 4ax, if p cos α + a sin² α = 0.

(vii) Angle θ between tangents at two points P(at₁t₂ , 2at₁) and Q(at₂², 2at₂) on the parabola y² = 4ax is given by

(viii) The combined equation of the pair of tangents drawn from a point to a parabola y² = 4ax is given by

SS₁ = T²

where, S = y² – 4ax, S₁= y₁² – 4ax₁

and T = [yy₁ – 2a (x + x₁)]

Important Results on Tangents

1. The tangent at any point on a parabola bisects the angle between the focal distance of the point and the perpendicular on the directrix from the point.
2. The tangent at the extremities of a focal chord of a parabola intersect at right angle on the directrix.
3. The portion of the tangent to a parabola cut off between the directrix and the curve subtends a right angle at the focus.
4. The perpendicular drawn from the focus on any tangent to a parabola intersect it at the point where it cuts the tangent at the vertex.
5. The orthocentre of any triangle formed by three tangents to a parabola lies on the directrix.
6. The circumcircle formed by the intersection points of tangents at any three points on a parabola passes through the focus of the parabola.
7. The tangent at any point of a parabola is equally inclined to the focal distance of the point and the axis of the parabola.
8. The length of the subtangent at any point on a parabola is equal to twice the abscissa of the point.
9. Two tangents can be drawn from a point to a parabola. Two tangents are real and distinct or coincident or imaginary according as given point lies outside, on or inside the parabola.

Equation of Normal

A line which is perpendicular to the tangent.

1. Point Form The equation of the normal to the parabola y² = 4ax at a point (x₁, y₁) is given by y – y₁ = -y₁/2a(x — x₁).
2. Parametric Form The equation of the normal to the parabola y² = 4ax at point (at², 2at) is given by y + tx = 2at + at³
3. Slope Form The equation of the normal to the parabola y² = 4ax in terms of its slope m is given by y = mx — 2am — am³ at point (am², — 2am).

Important Results on Normals

1. If the normal at the point P(at₁²,2at₁) meets the parabola y² = 4ax at Q(a₂²,2at₂), then t₂ = -t – 2/t₁.
2. The tangent at one extremity of the focal chord of a parabola is parallel to the normal at other extremity.
3. The normal at points P(at₁²,2at₁) and Q(a₂²,2at₂) to the parabola y² = 4ax intersect at the point
   [2a + a(t₁² + t₂²+ t₁t₂)], – at₁t₂(t₁ + t₂).
4. If the normal at points P(at₁²,2at₁) and Q(a₂²,2at₂) on the parabola y² = 4ax meet on the parabola, then t₁t₂ = 2.
5. If the normal at two points P and Q of a parabola y² = 4ax intersect at a third point R on the curve, then the product of the ordinates of P and Q is 8a².
6. If the normal chord at a point P(at² ,2at)to the parabola y² = 4ax subtends a right angle at the vertex of the parabola, then t² = 2.
7. The normal chord of a parabola at a point whose ordinate is equal to the abscissa, subtends a right angle at the focus.
8. The normal at any point of a parabola is equally inclined to the focal distance of the point and the axis of the parabola.
9. Three normals can be drawn from a point to a parabola.
10. Conormai The points on the parabola at which the normals pass through a common point are called conormal points. The conormal points are called the feet of the normals.

Points A, B and Care called conormal points.

• The algebraic sum of the slopes of the normals at conormals point is O.
• The sum of the ordinates of the conormal points is O.
• The centroid of the triangle formed by the conormal points on a parabola lies on its axis.

Director Circle

• The locus of the point of intersection of perpendicular tangents to a conic is known as director circle.
• The director circle of a parabola is its directrix.

Equation of Diameter

• The locus of mid-point of a system of parallel chords of a conic is known its diameter.
• The diameter bisecting chords of slope m to the parabola y² = 4ax is y = 2a/m

Length of Tangent and Normal

1. The length of the tangent = PT = PN cosec Ψ = y₁ cosec Ψ
2. The length of subtangent = NT = PN cot Ψ = y₁ cot Ψ
3. The length of normal = PG = PN sec Ψ = y₁ sec Ψ
4. The length of subnormal = NG = PN tan Ψ = y₁ tan Ψ

Pole and Polar

Let P be a point lying within or outside a given parabola. Suppose any straight line drawn through P intersects the parabola at Q and R. Then, the locus of the point of intersection of the tangents to the parabola at Q and R is called the polar of the given point P with respect to the parabola and the point P is called the pole of the polar.

1. The polar of a point P(x₁, ₁) with respect to the parabola y² = 4ax is yy₁ = 2a(x + x₁) or T = 0.
2. Any tangent is the polar of its point of contact.
3.  Pole of lx + my + n = 0 with respect to y² = 4ax is
4. Pole of the chord joining (x₁, y₁) and (x₁, y₁) is
5. If the polar of P(x₁, y₁)passes through Q(x₂ ,y₂), then the polar of Q will passes through P. Here, P and Q are called conjugate points.
6. If the pole of a line a₁x + b₁y + c₁ = 0 lies on another line a₂x + b₂y + c₂ = 0, then the pole of the second line will lies on the first line. Such lines are called conjugate lines.
7. The point of intersection of the polar of two points Q and R is the pole of QR.
8. The tangents at the ends of any chord of the parabola meet on the diameter which bisect the chord.

Important Points to be Remembered

(i) For the ends of latusrectum of the parabola y² = 4ax, the values of the perimeter are ± 1.
(ii) The circles described on focal radii of a parabola as diameter touches the tangent at the vertex.
(iii) The straight line y =mx + c meets the parabola y² = 4ax in two points. These two points are real and distinct, if c > a/m, points are real and coincident, if c = a/m, points are imaginary, if c < a/m.
(iv) Area of the triangle formed by three points on a parabola is twice the area of the triangle formed by the tangents at these points.
(v) The circles described on any focal chord of a parabola as diameter touches the directrix.
(vi) If y₁, y₂, y₃ are the ordinates of the vertices of a triangle inscribed in the parabola y² = 4ax, then its area is 1/8a (y₁ – y₂) (y₂ – y₃) (y₃ – y₁).

Circle is defined as the locus of a point which moves in a plane such that its distance from a fixed point in that plane is constant.

Standard Forms of a Circle

(i) Equation of circle having centre (h, k) and radius (x — h)² + (y — k)² = a².

If centre is (0, 0), then equation of circle is x² + y² = a².

(ii) When the circle passes through the origin, then equation of the circle is x² + y² — 2hx — 2ky = 0.

(iii) When the circle touches the X-axis, the equation is x² + y² — 2hx — 2ay + h² = O.

(iv) Equation of the circle, touching the Y-axis is x² + y² — 2ax — 2ky + k² = 0.

(v) Equation of the circle, touching both axes is x² + y² — 2ax — 2ay + a² = O.

(vi) Equation of the circle passing through the origin and centre lying on the X-axis is x² + y² — 2ax = O.

(vii) Equation of the circle passing through the origin and centre lying on the Y-axis is x² + y² – 2ay = 0.

(viii) Equation of the circle through the origin and cutting intercepts a and b on the coordinate axes is x² + y² — by = 0.

(ix) Equation of the circle, when the coordinates of end points of a diameter are (x₁, y₁) and (x₂, y₂) is

(x — x₁)(x — x₂) + (y – y₁)(y — y₂) = 0.

(x) Equation of the circle passes through three given points (x₁, y₁), (x₂, y₂) and (x₃, y₃) is

(xi) Parametric equation of a circle

(x – h)² + (y – k)² = a² is
x = h + a cosθ, y = k + a sinθ,
0 ≤ θ ≤ 2π
For circle x² + y² = a², parametric equation is
x = a cos θ, y = a sin θ

General Equation of a Circle

The general equation of a circle is given by x² + y² + 2gx + 2fy + c = 0, where centre of the circle = (- g, – f)

Radius of the circle = √g² + f² – c

1. If g² + f² – c > 0, then the radius of the circle is real and hence the circle is also real.
2. If g² + f² – c = 0, then the radius of the circle is 0 and the circle is known as point circle.
3. If g² + f² – c< 0, then the radius of the circle is imaginary. Such a circle is imaginary, which is not possible to draw.

Position of a Point with Respect to a Circle

A point (x₁, y₁) lies outside on or inside a circle

S ≡ x² + y² + 2gx + 2fy + c = 0, according as S₁ > , = or < 0
where, S₁ = x₁² + y₁² + 2gx₁, + 2fy₁+ c

Intercepts on the Axes

The length of the intercepts made by the circle x² + y² + 2gx + 2fy + c = 0 with X and Y-axes are

2√g² – c and 2√g² – c.

1. If g² > c, then the roots of the equation x² + 2gx + c = 0 are real and distinct, so the circle x² + y² + 2gx + 2fy + c = 0 meets the X-axis in two real and distinct points.
2. If g² = c, then the roots of the equation x² + 2gx + c = 0 are real and equal, so the circle touches X-axis, then intercept on X-axis is O.
3. If g² < c, then the roots of the equation x² + 2gx + c = 0 are imaginary, so the given circle does not meet X-axis in real point. Similarly, the circle x² + y² + 2gx + 2fy + c = 0 cuts the Y-axis in real and distinct points touches or does not meet in real point according to f² >, = or < c

Equation of Tangent

A line which touch only one point of a circle.

1. Point Form

1. The equation of the tangent at the point P(x₁, y₁) to a circle x² + y² 2gx + 2fy + c= 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
2. The equation of the tangent at the point P(x₁, y₁) to a circle x² + y² is xx₁ + yy₁ = r²

2. Slope Form

(i) The equation of the tangent of slope m to the circle x² + y² + 2gx + 2fy + c = 0

are y + f = m(x + g) ± √(g² + f² — c)(1 + m²)

(ii) The equation of the tangents of slope m to the circle (x – a)² (y – b)² = r² are y – b = m(x – a) ± r√(1 + m²) and the coordinates of the points of contact are

(iii) The equation of tangents of slope m to the circle x² + y² = r² are y = mx ± r√(1 + m²)and the coordinates of the point of contact are

3. Parametric Form

The equation of the tangent to the circle (x – a)² + (y – b)² = r² at the point (a + r cos θ, b + r sinθ) is (x – a) cos θ + (y – b) sin θ = r.

Equation of Normal

A line which is perpendicular to the tangent.

1. Point Form

1. (i) The equation of normal at the point (x₁, y₁) to the circle x² + y² + 2gx + 2fy + c = 0 is
   y – y₁ = [(y₁ + f)(x – x₁)]/(x₁ + g)
   (y₁ + f)x – (x₁ + g)y + (gy₁ – fx₁) = 0
2. (ii) The equation of normal at the point (x₁, y₁) to the circle
   x² + y² = r² is x/x₁ = y/y₁

2. Parametric Form

The equation of normal to the circle x² + y² = r² at the point (r cos θ, r sin θ) is

(x/r cos θ) = (y/r sin θ)

or y = x tan θ.

Important Points to be Remembered

(i) The line y = mx + c meets the circle in unique real point or touch the circle

x₂ + y₂ + r₂, if r = |c/√1 + m₂

and the point of contacts are

(ii) The line lx + my + n = 0 touches the circle x₂ + y₂ = r₂, if r₂(l₂ + m₂) = n₂.

(iii) Tangent at the point P (θ) to the circle x₂ + y₂ = r₂ is x cos θ + y sin θ = r.

(iv) The point of intersection of the tangent at the points P(θ₁) and Q(θ₂) on the circle x² + y² = r²

(v) Normal at any point on the circle is a straight line which is perpendicular to the tangent to the curve at the point and it passes through the centre of circle.

(vi) Power of a point (x₁, y₁) with respect to the circle x² + y² + 2gx + 2fy + c = 0 is x₁² + y₁² + 2gx₁ + 2fy₁ + c.

(vii) If P is a point and C is the centre of a circle of radius r, then the maximum and minimum distances of P from the circle are CP + r and CP — r , respectively.

(viii) If a line is perpendicular to the radius of a circle at its end points on the circle, then the line is a tangent to the circle and vice-versa.

Pair of Tangents

(i) The combined equation of the pair of tangents drawn from a point P(x₁, y₁) to the circle x² + y² = r² is

(x² + y² – r²)(x₁²+ y₁² – r₁²) = (xx₁ + yy₁ – r²)²
or SS₁ = T²
where, S = x² + y² – r², S₁ = x₁²+ y₁² – r₁²
and T = xx₁ + yy₁ – r²

(ii) The length of the tangents from the point P(x₁, y₁) to the circle x² + y² + 2gx + 2fy + c = 0 is equal to

(iii) Chord of contact TT’ of two tangents, drawn from P(x₁, y₁) to the circle x² + y² = r² or T = 0.

Similarly, for the circle

x² + y² + 2gx + 2fy + c = 0 is

xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0

(iv) Equation of Chord Bisected at a Given Point The equation of chord of the circle S ≡ x² + y² + 2gx + 2fy + c = 0 bisected at the point (x₁, y₁) is give by T = S₁.
i.e., xx₁ + yy₁ + g (x + x₁) + f (y + y₁) + c
= x₁² + y₁² + 2gx₁ + fy₁ + c

(v) Director Circle The locus of the point of intersection of two perpendicular tangents to a given circle is called a director circle. For circle x² + y² = r², the equation of director circle is x² + y² = 2r².

Common Chord

The chord joining the points of intersection of two given circles is called common chord.

(i) If S₁ = 0 and S₁ = 0 be two circles, such that

S₁ ≡ x² + y² + 2g₁x + 2f₁y + c₁ = 0
and S₂ ≡ x² + y² + 2g₂x + 2f₂y + c₂ = 0
then their common chord is given by S₁ — S₂ = 0

(ii) If C₁, C₂ denote the centre of the given circles, then their common chord

PQ = 2 PM = 2√(C₁P)² – C₁M)²

(iii) If r₁, and r₂ be the radii of ‘two circles, then length of common chord is

Angle of Intersection of Two Circles

The angle of intersection of two circles is defined as the angle between the tangents to the two circles at their point of intersection is given by

cos θ = (r₁² + r₂² – d²)/(2r₁r₂)

Orthogonal Circles

Two circles are said to be intersect orthogonally, if their angle of intersection is a right angle.

If two circles

S₁ ≡ x² + y² + 2g₁x + 2f₁y + C₁ = 0 and

S₂ ≡ x² + y² + 2g₂x + 2f₂y + C₂ = 0 are orthogonal, then 2g₁g₂ + 2f₁f₂ = c₁ + c₂

Family of Circles

(i) The equation of a family of circles passing through the intersection of a circle x² + y² + 2gx + 2fy + c = 0 and line

L = lx + my + n = 0 is S + λL = 0

where, X, is any real number.

(ii) The equation of the family of circles passing through the point A(x₁, y₁) and B (x₁, y₁) is

(iii) The equation of the family of -circles touching the circle

S ≡ x² + y² + 2gx + 2fy + c = 0 at point P(x₁, Y₁) is

xx² + y² + 2gx + 2fy + c + λ, [xx₁ + yy₁ + g(x + x₁) + f(Y+ Y₁) + c] = 0 or S + λL = 0, where L = 0 is the equation of the tangent to

S = 0 at (x₁, y₁) and X ∈ R

(iv) Any circle passing through the point of intersection of two circles S₁ and S₂ is S₁ +λ(S₁— S₂) = 0.

Radical Axis

The radical axis of two circles is the locus of a point which moves in such a way that the length of the tangents drawn from it to the two circles are equal.

A system of circles in which every pair has the same radical axis is called a coaxial system of circles.

The radical axis of two circles S₁ = 0 and S₂ = 0 is given by S₁ — S₂ = 0.

1. The radical axis of two circles is always perpendicular to the line joining the centres of the circles.
2. The radical axis of three vertices, whose centres are non-collinear taken in pairs of concurrent.
3. The centre of the circle cutting two given circles orthogonally, lies on their radical axis.
4. Radical Centre The point of intersection of radical axis of three circles whose centre are non-collinear, taken in pairs, is called their radical centre.

Pole and Polar

If through a point P (x₁, y₁) (within or outside a circle) there be drawn any straight line to meet the given circle at Q and R, the locus of the point of intersection of tangents at Q and R is called the polar of P and po.:.at P is called the pole of polar.

1. Equation of polar to the circle x² + y² = r² is xx₁ + yy₁ = r².
2. Equation of polar to the circle x² + y² + 2gx + 2fy + c = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0
3. Conjugate Points Two points A and B are conjugate points with respect to a given circle, if each lies on the polar of the other with respect to the circle.
4. Conjugate Lines If two lines be such that the pole of one lies on the other, then they are called conjugate lines with respect to the given circle.

Coaxial System of Circles

A system of circle is said to be coaxial system of circles, if every pair of the circles in the system has same radical axis.

1. The equation of a system of coaxial circles, when the equation of the radical axis P ≡ lx + my + n = 0 and one of the circle of the system S = x² + y² + 2gx + 2fy + c = 0, is S + λP = 0.
2. Since, the lines joining the centres of two circles is perpendicular to their radical axis. Therefore, the centres of all circles of a coaxial system lie on a straight line, which is perpendicular to the common radical axis.

Limiting Points

Limiting points of a system of coaxial circles are the centres of the point circles belonging to the family.

Let equation of circle be x² + y² + 2gx + c = 0

∴ Radius of circle = √g² — c

For limiting point, r = 0

∴ √g² — c = 0 &rArr;g = ± √c

Thus, limiting points of the given coaxial system as (√c, 0) and (—√c, 0).

Important Points to be Remembered

(i) Circle touching a line L=O at a point (x₁, y₁) on it is

(x — x₁)² + (y — y₁)² + XL = 0.

(ii) Circumcircle of a A with vertices (x₁, y₁), (x₂, y₂), (x₃, y₃) is

(iii) A line intersect a given circle at two distinct real points, if the length of the perpendicular from the centre is less than the radius of the circle.

(iv) Length of the intercept cut off from the line y = mx + c by the circle x² + y² = a² is

(v) In general, two tangents can be drawn to a circle from a given point in its plane. If m₁and m₂ are slope of the tangents drawn from the point P(x₁, y₁) to the circle x² + y² = a², then

(vi) Pole of lx + my + n = 0 with respect to x² + y² = a² is

(vii) Let S₁ = 0, S₂ = 0 be two circles with radii r₁ , r₂, then S₁/r₁ ± S₂/r₂ = 0 will meet at right angle.

(viii) The angle between the two tangents from (x₁, y₁) to the circle x² + y² = a² is 2 tan^-1 (a/√S₁).

(ix) The pair of tangents from (0, 0) to the circle x² + y² + 2gx + 2fy + c = 0 are at right angle, if g² + f² = 2c.

(x) If (x₁, y₁) is one end of a diameter of the circle x² + y² + 2gx + 2fy + c = 0, then the other end will be (-2g – x₁, -2f – y₁).

Image of the Circle by the Line Minor

Let the circle be x² + y² + 2gx + 2fy + c = 0

and line minor lx + my + n = 0.

Then, the image of the circle is

(x — X₁)² + (y — y₁)² =r²

where, r = √g² + f² — c

Diameter of a Circle

The locus of the middle points of a system of parallel chords of a circle is called a diameter of the circle.

(i) The equation of the diameter bisecting parallel chords y = mx + c of the circle x² + y² = a² is x + my = 0.

(ii) The diameter corresponding to a system of parallel chords of a circle always passes through the centre of the circle and is perpendicular to the parallel chords.

Common Tangents of Two Circles

Let the centres and radii of two circles are C₁, C₂ and r₁, r₂, respectively.

1. (i) When one circle contains another circle, no common tangent is possible.
   Condition, C₁C₂ < r₁ – r₂
2. (ii) When two circles touch internally, one common tangent is possible.
   Condition , C₁C₂ = r₁ – r₂
3. (iii) When two circles intersect, two common tangents are possible.
   Condition, |r₁ — r₂| < C₁C₂ < |r₁ + r₂|
4. (iv) When two circles touch externally, three common tangents are possible.
   Condition, C₁C₂ = r₁ + r₂
5. (v) When two circles are separately, four common tangents are possible.
   Condition, C₁C₂ > r₁ + r₂

Important Points to be Remembered

Let AS is a chord of contact of tangents from C to the circle x² + y² = r². M is the mid-point of AB.

Coordinate Geometry

The branch of Mathematics in which geometrical problem are solved through algebra by using the coordinate system, is known as coordinate geometry.

Rectangular Axis

Let XOX’ and YOY’ be two fixed straight lines, which meet at right angles at O. Then,

(i) X’OX is called axis of X or the X-axis or abscissa.

(ii) Y’OY is called axis of Yor the Y-axis or ordinate.

(iii) The ordered pair of real numbers (x, y) is called cartesian coordinate .

Quadrants

The X and Y-axes divide the coordinate plane into four parts, each part is called a quadrant which is given below.

Polar Coordinates

In ΔOPQ,

cos θ = x / r and sin θ = y / r ⇒ x = r cos θ and y = r sin θ

where, r = √x² + y²

The polar coordinate is represented by the symbol P(r,θ).

Distance Formula

(i) Distance between two points P (x₁, y₁) and Q (x₂, y₂), is

√(x₂ – x₁)² + (y₂ – y₁)².

(ii) If points are (r₁ , θ₁) arid (r₂, θ₂), then distance between them is

√r²₁ + r²₂ – 2r₁r₂cos(θ₁ – θ₂).

(iii) Distance of a point (x₁, y₁) from the origin is √x²₁ + y²₁.

Section Formula

(i) The coordinate of the point which divides the joint of (x₁, y₁) and (x₂, y₂) in the ratio m₁: m₂ internally, is

(ii) X-axis divides the line segment joining (x₁, y₁) and (x₂, y₂) in the ratio – y_{1 : y2.}

Similarly, Y-axis divides the same line segment in the ratio – x_{1 : x2.}

(iii) Mid-point of the joint of (x₁, y₁) and (x₂, y₂) is (x₁ + x₂ / 2 , y₁ + y₂ / 2)

(iv) Centroid of ΔABC with vertices (x₁, y₁), (x₂, y₂) and (x₃, y₃), is

(x₁ + x₂ + x₃ / 3 , y₁ + y₂ + y₃ / 3).

(v) Circumcentre of ΔABC with vertices A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃), is

(vi) Incentre of Δ ABC with vertices A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) and whose sides are a, band c, is

(ax₁ + bx₂ + cx₃ / a + b + c , ay₁ + by₂ + cy₃ / a + b + c).

(vii) Excentre of ΔABC with vertices A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) and whose sides are a, band c, is given by

Area of Triangle/Quadrilateral

(i) Area of ΔABC with vertices A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃), is

These points A, Band C will be collinear, if Δ = O.

(ii) Area of the quadrilateral formed by joining the vertices

(iii) Area of trapezium formed by joining the vertices

Shifting/Rotation of Origin/Axes

Shifting of Origin

Let the origin is shifted to a point O'(h, k). If P(x, y) are coordinates of a point referred to old axes and P’ (X, Y) are the coordinates of the same points referred to new axes, then

Rotation of Axes

Let (x, y) be the coordinates of any point P referred to the old axes and (X, Y) be its coordinates referred to the new axes (after rotating the old axes by angle θ). Then,

X = x cos θ + y sin θ and Y = y cos θ + x sin θ

Shifting of Origin and Rotation of Axes

If origin is shifted to point (h, k) and system is also rotated by an angle θ in anti-clockwise, then coordinate of new point P’ (x’, y’) is obtained by replacing

x’= h + x cos θ + y sin θ

and y’ = k – x sin θ + y cos θ

Locus

The curve described by a point which moves under given condition(s) is called its locus.

Equation of Locus

The equation of the locus of a point which is satisfied by the coordinates of every point.

Algorithm to Find the Locus of a Point

Step I Assume the coordinates of the point say (h,k) whose locus is to be found.

Step II Write the given condition in mathematical form involving h, k.

Step III Eliminate the variable(s), if any.

Step IV Replace h by x and k by y in the result obtained in step III. The equation so obtained is the locus of the point, which moves under some stated condition(s).

Straight Line

Any curve is said to be a straight line, if two points are taken on the curve such that every point on the line segment joining any two points on it lies on the curve.

General equation of a line is ax + by + c = o.

Slope (Gradient) of a Line )

The trigonometric tangent of the angle that a line makes with the positive direction of the X-axis in anti-clockwise sense is called the slope or gradient of the line.

So, slope of a line, m = tan θ

where, θ is the angle made by the line with positive direction of X-axis.

Important Results on Slope of Line

(i) Slope of a line parallel to X-axis, m = 0.
(ii) Slope of a line parallel to Y-axis, m = ∞.
(iii) Slope of a line equally inclined with axes is 1 or -1 as it makes an angle of 45° or 135°, with X-axis.
(iV) Slope of a line passing through (x, y,) and (x₂, y₂) is given by

m = tan θ = y₂ – y₁ / x₂ – x₁.

Angle between Two Lines

The angle e between two lines having slopes m₁ and m₂ is

(i) Two lines are parallel, iff m₁ = m₂.
(ii) Two lines are perpendicular to each other, iff m₁m₂ = – 1.

Equation of a Straight Line

General equation of a straight line is Ax + By + C = 0.

(i) The equation of a line parallel to X-axis at a distance b from it, is given by

y = b

(ii) The equation of a line parallel to Y-axis at a distance a from it, is given by

x = a

(iii) Equation of X-axis is

y = 0

(iv) Equation of Y-axis is

x = 0

Different Form of the Equation of a Straight Line

(i) Slope Intercept Form The equation of a line with slope m and making an intercept c on Y-axis, is

y = mx + c

If the line passes through the origin, then its equation will be

y= mx

(ii) One Point Slope Form The equation of a line which passes through the point (x₁, y₁) and has the slope of m is given by

(y – y₁) = m (x – x₁)

(iii) Two Points Form The equation of a line’ passing through the points (x₁, y₁) and (x₂, y₂) is given by

(y – y₁) = (y₂ – y₁ / x₂ – x₁) (x – x₁)

This equation can also be determined by the determinant method, that is

(iv) The Intercept Form The equation of a line which cuts off intercept a and b respectively on the X and Y-axes is given by

x / a + y / b = 1

The general equation Ax + By + C = 0 can be converted into the intercept form, as

x / – (C A) + y / – (C B) = 1

(v) The Normal Form The equation of a straight line upon which the length of the perpendicular from the origin is p and angle made by this perpendicular to the X-axis is α, is given by

x cos α + Y sin α = p

(vi) The Distance (Parametric) Form The equation of a straight line passing through (x₁, y₁) and making an angle θ with the positive direction of x-axis, is

x – x₁ / cos θ = y – y₁ / sin θ = r

where, r is the distance between two points P(x, y) and Q(x₁, y₁).

Thus, the coordinates of any point on the line at a distance r from the given point (x₁, y₁) are (x₁ + r cos θ, y₁ + r sin θ). If P is on the right side of (x₁, y₁) then r is positive and if P is on the left side of (x₁, y₁) then r is negative.

Position of Point(s) Relative to a Given Line

Let the equation of the given line be ax + by + C = 0 and let the Coordinates of the two given points be P(x₁, y₁) and Q(x₂, y₂).

(i) The two points are on the same side of the straight line ax + by + c = 0, if ax₁ + by₁ + c and ax₂ + by₂ + c have the same sign.

(ii) The two points are on the opposite side of the straight line ax + by + c = 0, if ax₁ + by₁ + c and ax₂ + by₂ + c have opposite sign.

(iii) A point (x₁, y₁) will lie on the side of the origin relative to a line ax + by + c = 0, if ax₁+ by₁ + c and c have the same sign.

(iv) A point (x₁, y₁) will lie on the opposite side of the origin relative to a line ax + by + c = 0, if ax₁ + by₁ + c and c have the opposite sign.

(v) Condition of concurrency for three given lines ax₁ + by₁ + c₁ = 0, ax₂ + by₂ + c₂ and ax₃ + by₃ + c₃ = 0 is a₃(b₁c₂ – b₂c₁) + b₃(c₁a₂ – a₁c₂) + c₃(a₁b₂ – a₂b₁) = 0

or

(vi) Point of Intersection of Two Lines Let equation of lines be ax₁ + by₁ + c₁ = 0 and ax₂ + by₂ + c₂ = 0, then their point of intersection is

(b₁c₂ – b₂c₁ / a₁b₂ – a₂b₁, c₁a₂ – c₂a₁ / a₁b₂ – a₂b₁).

Line Parallel and Perpendicular to a Given Line

(i) The equation of a line parallel to a given line ax + by + c = 0 is ax + by + λ = 0, where λ is a constant.

(ii) The equation of a line perpendicular to a given line ax + by + c = is bx – ay + λ = 0, where λ is a constant.

Image of a Point with Respect to a Line

Let the image of a point (x₁, y₁) with respect to ax + by + c = 0 be (x₂, y₂), then

x₂ – x₁ / a = y₂ – y₁ / b = – 2 (ax₁ + by₁ + c) / a² + b²

(i) The image of the point P(x₁, y₁) with respect to X-axis is Q(x₁ – y₁).

(ii) The image of the point P(x₁, y₁) with respect to Y-axis is Q(-x₁, y₁).

(iii) The image of the point P(x₁, y₁) with respect to mirror Y = x is Q(y₁, x₁).

(iv) The image. of the point P(x₁, y₁) with respect to the line mirror y == x tan θ is

x = x₁ cos 2θ + y₁ sin 2θ
Y = x₁ sin 2θ – y₁ cos 2θ

(v) The image of the point P(x₁, y₁) with respect to the origin is the point (-x₁, y₁).

(vi) The length of perpendicular from a point (x₁, y₁) to a line ax + by + c = 0 is

Equation of the Bisectors

The equation of the bisectors of the angle between the lines

a₁x + b₁y + c₁ = 0

and a₂x + b₂y + c₂ = 0

are given by

a₁x + b₁y + c₁ / √a²₁ + b²₁ = &plusmn a₂x + b₂y + c₂ / √a²₂ + b²₂

(i) If a₁ a₂ + b₁ b₂ > 0, then we take positive sign for obtuse and negative sign for acute.

(ii) If a₁ a₂ + b₁ b₂ < 0, then we take negative sign for obtuse and positive sign for acute .

Pair of Lines

General equation of a pair of straight lines is ax² + 2hxy + by² + 2gx + 2fy + c = 0.

Homogeneous Equation of Second Degree

A rational, integral, algebraic equation in two variables x and y is said to be a homogeneous equation of the second degree, if the sum of the indices of x and y in each term is equal to 2.

The general form of homogeneous equation of the second degree x and y is ax² + 2hxy + by² = 0, which passes through the origin.

Important Properties

If ax² + 2hxy + by² = 0 be an equation of pair of straight lines.

(i) Slope of first line, m₁ = – h + √h² – ab / b

and slope of second line, m₂ = – h – √h² – ab / b

m₁ + m₂ = – 2h / b = – Coefficient of xy / Coefficient of y²

and m₁ m₂ = a / b = Coefficient of x² / Coefficient of y²

Here, m₁ and m₂ are

(a) real and distinct, if h² > ab.

(b) coincident, if h² = ab.

(c) imaginary, if h² < ab.

(ii) Angle between the pair of lines is given by

tan θ = ²√h² – ab / a + b

(a) If lines are coincident, then h² = ab
(b) If lines are perpendicular, then a + b = o.

(iii) The joint equation of bisector of the angles between the lines represented by the equation ax² + 2hxy + by² = 0 is

x² – b² / a – b = xy / h ⇒ hx² – (a – b)xy – hy²=0.

(iv) The necessary and sufficient condition ax² + 2hxy + by² + 2gx + 2fy + C = 0 to represent a pair of straight lines, if abc + 2fgh – af² – bg² – ch² = 0

or

(v) The equation of the bisectors of the angles between the lines represented by ax² + 2hxy + by² + 2gx + 2fy + c = 0 are given by

(x – x¹)² – (y – y¹)² / a – b = (x – x¹) (y – y¹) / h,

where, (x¹, y¹) is the point of intersection of the lines represented by the given equation.

(vi) The general equation ax² + 2hxy + by² + 2gx + 2fy + C = 0 will represent two parallel lines, if g² – ac > 0 and a / h = h / b = g / f and the distance between them is 2√g² – ac / a(a + b) or 2√f² – bc / b(a + b).

(vii) If the equation of a pair of straight lines is ax² + 2hxy + by² + 2gx + 2fy + C = 0, then the point of intersection is given by

(hf – bg / ab – h², gh – af / ab – h²).

(viii) The equation of the pair of lines through the origin and perpendicular to the pair of lines given by ax² + 2hxy + by² = 0 is bx² – 2hxy + ay² = 0.

(ix) Equation of the straight lines having the origin to the points of intersection of a second degree curve ax² + 2hxy + by² + 2gx + 2fy + c = 0 and a straight line Lx + my + n = 0 is

ax² + 2hxy + by² + 2gx(Lx + my / – n) + 2fy(Lx + my / – n) + c (Lx + my / – n)² = 0.

Important Points to be Remembered

1. A triangle is an isosceles, if any two of its median are equal.

2. In an equilateral triangle, orthocentre, centroid, circumcentre, incentre coincide.

3. The circumcentre of a right angled triangle is the mid-point of the hypotenuse.

4. Orthocentre, centroid, circumcentre of a triangle are collinear, Centroid divides the line joining orthocentre and circumcentre in the ratio 2: 1.

5. If D, E and F are the mid-point of the sides BC, CA and AB of MBC, then the centroid of Δ ABC = centroid of Δ DEF.

6. Orthocentre of the right angled Δ ABC, right angled at A is A

7. Circumcentre of the right angled Δ ABC, right angled at A is B + C / 2.

8. The distance of a point (x¹, y¹) from the ax + by + c = 0 is

d = |ax₁ + by₁ + c / √a² + b²|

9. Distance between two parallel lines a₁x + b₁y + c₁ = 0 and a₁x + b₁y + c₂ = 0 is given by

d = |c₂ – c₁ / √a² + b²|.

10. The area of the triangle formed by the lines y =m₁x + c₁, y = m₂x + c₂ and y = m₃x + c₃ is .

.

11. Area of the triangle formed by the line ax + by + c = 0 with the coordinate axes is Δ = c² / 2|ab|.

12. The foot of the perpendicular(h,k) from (x₁, y₁) to the line ax + by + c = 0 is given by h – x₁ / a = k – y₁ / b = – (ax₁ + by₁ + c) / a² + b².

13. Area of rhombus formed by ax ± by ± c = 0 is |2c² / ab|.

14. Area of the parallelogram formed by the lines

a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0, a₁x + b₁y + d₁ = 0 and a₂x + b₂y + d₂ = 0 is

|(d₁ – c₁) (d₂ – c₂ / a₁b₂ – a₂b₁|.

15. (a) Foot of the perpendicular from (a, b) on x – y = 0 is

(a + b / 2, a + b / 2).

(b) Foot of the perpendicular from (a,b) on x + y = 0 is

(a – b / 2, a – b / 2).

16. The image of the line a₁x + b₁y + c₁ = 0 about the line ax + by + c = 0 is .

2(aa₁ + bb₁) (ax + by + c) =(a²+ b²) (a₁x + b₁y + c₁).

17. Given two vertices (x₁, y₁) and (x₂, y₂) of an equilateral MBC, then its third vertex is given by.

[x₁ + x₂ ± √3 (y₁ – y₂) / 2, y₁ + y₂ ∓ √3 (x₁ – x₂) / 2]

18. The equation of the straight line which passes through a given point (x₁, y₁) and makes an angle α with the given straight line y = mx + c are

19. The equation of the family of lines passing through the intersection of the lines a₁x + b₁y+ c₁ = 0 and a₂x + b₂y + c₂ = 0 is

(a₁x + b₁y+ c₁) + l(a₂x + b₂y + c₂) = 0

where, λ is any real number.

20. Line ax + by + c = 0 divides the line joining the points (x₁, y₁) and (x₂, y₂) in the ratio λ : 1, then λ = – (a₁x + b₁y+ c / a₂x + b₂y + c).

If λ is positive it divides internally and if λ. is negative, then it divides externally.

21. Area of a polygon of n-sides with vertices A₁(x₁, y₁), A₂ (x₂, y₂) ,… ,A_n(x_n, y_n)

22. Equation of the pair of lines through (α, β) and perpendicular to the pair of lines ax² + 2hxy + by² = 0 is b (x – α}² – 2h (x – α)(y – β) + a (y – β)²= 0.