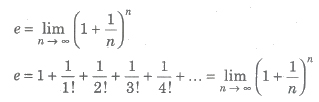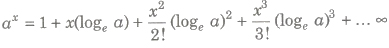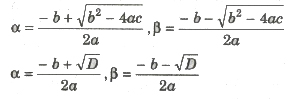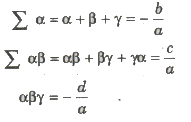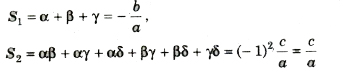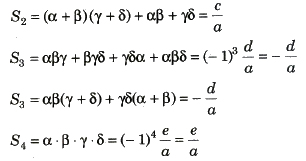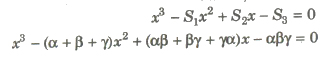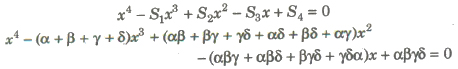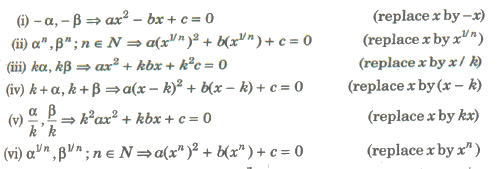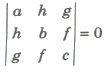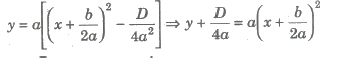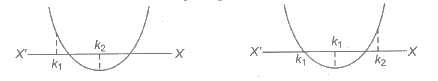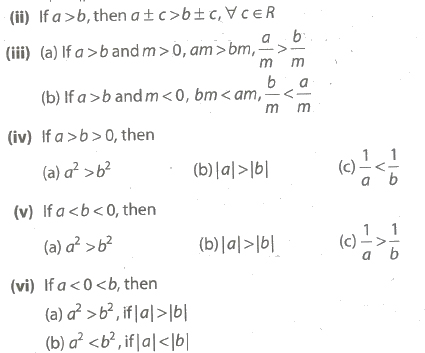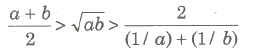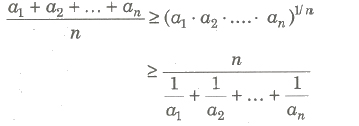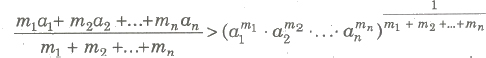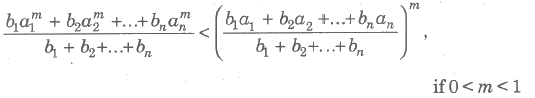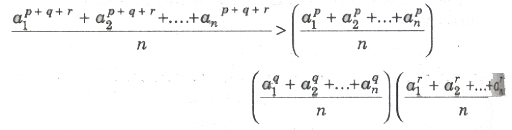1. Real Polynomial: Let a0, a1, a2, … , an be real numbers and x is a real variable. Then, f(x) = a0 + a1x + a2x2 + … + anxn is called a real polynomial of real variable x with real coefficients.
2. Complex Polynomial: If a0, a1, a2, … , an be complex numbers and x is a varying complex number, then f(x) = a0 + a1x + a2x2 + … + an – 1xn – 1 + anxn is called a complex polynomial or a polynomial of complex variable with complex coefficients.
3. Degree of a Polynomial: A polynomial f(x) = a0 + a1x + a2x2 + a3x3 + … + anxn , real or complex is a polynomial of degree n , if an ≠ 0.
4. Polynomial Equation: If f(x) is a polynomial, real or complex, then f(x) = 0 is called a polynomial equation. If f(x) is a polynomial of second degree, then f(x) = 0 is called a quadratic equation .
Quadratic Equation: A polynomial of second degree is called a quadratic polynomial. Polynomials of degree three and four are known as cubic and biquadratic polynomials respectively. A quadratic polynomial f(x) when equated to zero is called quadratic equation. i.e., ax2 + bx + c = 0 where a ≠ 0.
Roots of a Quadratic Equation: The values of variable x .which satisfy the quadratic equation is called roots of quadratic equation.
Important Points to be Remembered
- An equation of degree n has n roots, real or imaginary .
- Surd and imaginary roots always occur in pairs of a polynomial equation with real coefficients i.e., if (√2 + √3i) is a root of an equation, then’ (√2 – √3i) is also its root. .
- An odd degree equation has at least one real root whose sign is opposite to that of its last’ term (constant term), provided that the coefficient of highest degree term is positive.
- Every equation of an even degree whose constant term is negative and the coefficient of highest degree term is positive has at least two real roots, one positive and one negative.
- If an equation has only one change of sign it has one positive root.
- If all the terms of an equation are positive and the equation involves odd powers of x, then all its roots are complex.
Solution of Quadratic Equation
1.Factorization Method: Let ax2 + bx + c = α(x – α) (x – β) = O. Then, x = α and x = β will satisfy the given equation.
2. Direct Formula: Quadratic equation ax2 + bx + c = 0 (a ≠ 0) has two roots, given by
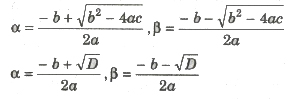
where D = Δ = b2 – 4ac is called discriminant of the equation .
Above formulas also known as Sridharacharya formula.
Nature of Roots
Let quadratic equation be ax2 + bx + c = 0, whose discriminant is D.
(i) For ax2 + bx + c = 0; a, b , C ∈ R and a ≠ 0, if
(a) D < => Complex roots
(b) D > 0 => Real and distinct roots
(c) D = 0 => Real and equal roots as α = β = – b/2a
(ii) If a, b, C ∈ Q, a ≠ 0, then
(a) If D > 0 and D is a perfect square => Roots are unequal and rational.
(b) If D > 0, a = 1; b, c ∈ I and D is a perfect square. => Roots are integral. .
(c) If D > and D is not a perfect square. => Roots are irrational and unequal.
(iii) Conjugate Roots The irrational and complex roots of a quadratic equation always occur in pairs. Therefore,
(a) If one root be α + iβ, then other root will be α – iβ.
(b) If one root be α + √β, then other root will be α – √β.
(iv) If D, and D2 be the discriminants of two quadratic equations, then
(a) If D1 + D2 ≥ 0, then At least one of D1 and D2 ≥ 0 If D1 < 0, then D2 > 0 ,
(b) If D1 + D2 < 0, then At least one of D1 and D2 < 0 If D1 > 0, then D2 < 0
Roots Under Particular Conditions
For the quadratic equation ax2 + bx + e = 0.
(i) If b = 0 => Roots are real/complex as (c < 0/c > 0) and equal in magnitude but of opposite sign.
(ii) If c = 0 => One roots is zero, other is – b / a.
(iii) If b = C = 0 => Both roots are zero.
(iv) If a = c => Roots are reciprocal to each other.
(v) If a > 0, c < 0, a < 0, c > 0} => Roots are of opposite sign.
(vi) If a > 0, b > 0, c > 0, a < 0, b < 0, c < 0} => Both roots are negative, provided D ≥ 0
(vii) If a > 0, b < 0, c > 0, a < 0, b > 0, c < 0} => Both roots are positive, provided D ≥ 0
(viii) If sign of a = sign of b ≠ sign of c => Greater root in magnitude is negative.
(ix) If sign of b = sign of c ≠. sign of a => Greater root in magnitude is positive.
(x) If a + b + c = 0 => One root is 1 and second root is c/a.
Relation between Roots and Coefficients
1. Quadratic Equation: If roots of quadratic equation ax2 + bx + c = 0 (a ≠ 0) are α and β, then Sum of roost = S = α + β = -b/a = – coefficient of x / coefficient of x2 Product of roots = P = α * β = c/a = constant term / coefficient of x2
2. Cubic Equation: If α, β and γ are the roots of cubic equation ax3 + bx2 + cx + d = 0.
Then,
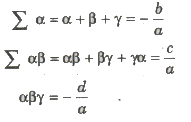
3. Biquadratic Equation: If α, β, γ and δ are the roots of the biquadratic equation ax4 + bx3 + cx2 + dx + e = 0, then
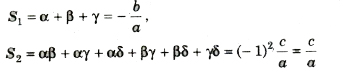
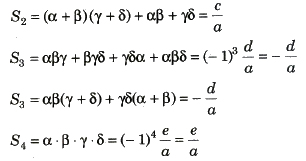
Symmetric Roots: If roots of quadratic equation ax2 + bx + c = 0 (a ≠ 0) are α and β, then
Formation of Polynomial Equation from Given Roots
If a1, a2 a3,…, an are the roots of an nth degree equation, then the equation is xn – S1Xn – 1+ S2Xn – 2 – S3Xn – 3 +…+( _l)n Sn = 0 where Sn denotes the sum of the products of roots taken n at a time.
1. Quadratic Equation
If α and β are the roots of ‘a quadratic equation, then the equation is x2 – S1X + S2 = 0
i.e., x2 – (α + β) x + αβ = 0
2. Cubic Equation
If α, β and γ are the roots of cubic equation, then the equation is
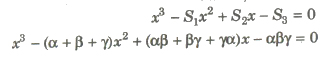
3. Biquadratic Equation
If α, β, γ and δ are the roots of a biquadratic equation, then the equation is
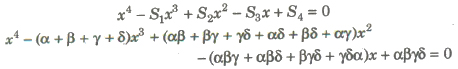
Equation In Terms of the Roots of another Equation
If α, β are roots of the equation ax2 + bx + c = 0, then the equation whose roots are.
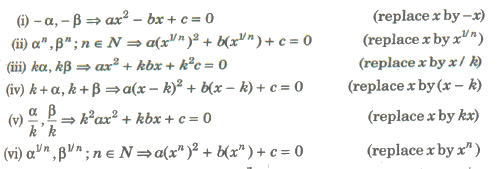
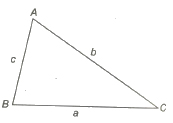
The quadratic function f(x) = ax2 + 2hxy + by2 + 2gx + 2fy + c is always resolvable into linear factor, iff
abc + 2fgh – af2 – bg2 – ch2 = 0
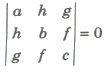
Condition for Common Roots in a Quadratic Equation
1. Only One Root is Common
If α be the common root of quadratic equations
a1x2 + b1x + C1 = 0,
and a2x2 + b2x + C2 = 0,
then a1a2 + b1α + C1 = 0,
and a2a2 + b2α + C2 = 0,
By Cramer’s Rule
Hence, the condition for only one root common is
(c1a2 – c2a1)2 = (b1c2 – b2c1)(a1b2 – a2b1)
2. Both Roots are Common
The required condition is
a1 / a2 = b1 / b2 = c1 / c2
(i) To find the common root of two equations, make the coefficient of second degree term in the two equations equal and subtract. The value of x obtained is the required common root.
(ii) Two different quadratic equations with rational coefficient can not have single common root which is complex or irrational as imaginary and surd roots always occur in pair.
Properties of Quadratic Equation
(i) f(a) . f(b) < 0, then at least one or in general odd number of roots of the equation f(x) = 0 lies between a and b.
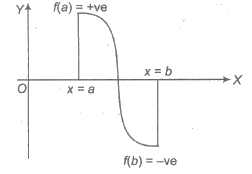
(ii) f( a) . f( b) > 0, then in general even number of roots of the equation f(x) = 0 lies between a and b or no root exist f(a) = f(b), then there exists a point c between a and b such that f'(c) = 0, a < c < b.
(iii) If the roots of the quadratic equation a1x2 + b1x + c1 = 0, a2x2 + b2x + c2 = 0 are in the ratio (i.e., &alpha1;/β1 = &alpha2;/β2), then
b12 / b22 = a1c1 / a2c2.
(iv) If one root is k times the other root of the quadratic equation ax2 + bx + c = 0 ,then
(k + 1)2 / k = b2 / ac
Quadratic Expression
An expression of the form ax2 + bx + c, where a, b, c ∈ R and a ≠ 0 is called a quadratic expression in x .
1. Graph of a Quadratic Expression
We have
y = ax2 + bx + c = f(x)
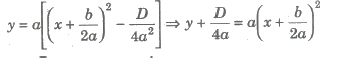
Let y + D/4a = Y and x + D / 2a = X
Y = a * X2 => X2 = Y / a
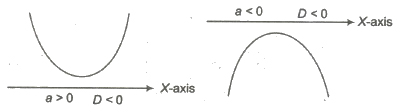
(i) The graph of the curve y = f(x) is parabolic.
(ii) The axis of parabola is X = 0 or x + b / 2a = 0 i.e., (parallel to Y-axis). •
(iii) If a > 0, then the parabola opens upward.
If a < 0, then the parabola opens downward.
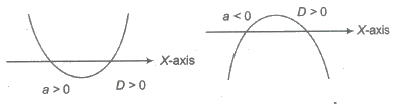
2. Position of y = ax2 +bx + c with Respect to Axes.
(i) For D > 0, parabola cuts X-axis in two real and distinct points
i.e, x = -b ± √D / 2a
(ii) For D = 0, parabola touch X-axis in one point, x = – b/2a.
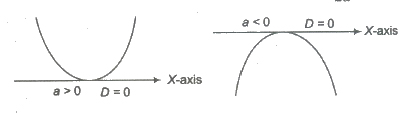
(iii) For D < O,parabola does not cut X-axis (i.e., imaginary value of x).
3. Maximum and Minimum Values of Quadratic Expression
(i) If a > 0, quadratic expression has least value at x = b / 2a. This least value is given by 4ac – b2 / 4a = – D/4a. But their is no greatest
value.
(ii) If a < 0, quadratic expression has greatest value at x = – b/2a . This greatest value is given by 4ac – b2 / 4a = – D/4a. But their is no least value.
4. Sign of Quadratic Expression
(i) a > 0 and D < 0, so f(x) > 0 for all x ∈ R i.e., f(x) is positive for all real values of x.
(ii) a < 0 and D < 0, so f(x) < 0 for all x ∈ R i.e., f(x) is negative for all real values of x.
(iii) a > 0 and D = 0, so f(x) ≥ 0 for all x ∈ R i.e., f(x) is positive for all real values of x except at vertex, where f(x) = 0.
(iv) a < 0 and D = 0, so f(x) ≤ 0 for all x ∈ R i.e., f(x) is negative for all real values of x except at vertex, where f(x) = 0.
(v) a > 0 and D > 0
Let f(x) = o have two real roots α and β (α < β), then f(x) > 0 for x ∈ (- ∞, α) ∪ (β,∞) and f (x) < 0 for all x ∈ (α, β).
(vi) a < 0 and D > 0
Let f(x) = 0 have two real roots α and β (α < β). Then, f(x) < 0 for all x ∈ (- ∞, α) ∪ (β,∞) and f(x) > 0 for all
x ∈ (α, β). ,
5. Intervals of Roots
In some problems, we want the roots of the equation ax2 + bx + c = 0 to lie in a given interval. For this we impose conditions on a, b and c.
Since, a ≠ 0, we can take f(x) = x2 + b/a x + c/a.
(i) Both the roots are positive i.e., they lie in (0,∞), if and only if roots are real, the sum of the roots as well as the product of the roots is positive.
α + β = -b/a > 0 and αβ = c/a > 0 with b2 – 4ac ≥ 0
Similarly, both the roots are negative i.e., they lie in (- ∞,0) ifF roots are real, the sum of the roots is negative and the product of the roots is positive.
i.e., α + β = -b/a < 0 and αβ = c/a > 0 with b2 – 4ac ≥ 0
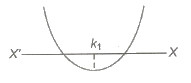
(ii) Both the roots are greater than a given number k, iFf the following conditions are satisfied
D ≥ 0, -b/2a > k and f(k) > 0
(iii) Both .the roots are less than a given number k, iff the following conditions are satisfied
D ≥ 0, -b/2a > k and f(k) > 0
(iv) Both the roots lie in a’ given interval (k1, k2), iff the following conditions are satisfied
D ≥ 0,k1 < -b/2a < k2 and f(k1) > 0, f(k2) > 0
(v) Exactly one of the roots lie in a given interval (k1, k2), iff
f(k1) f(k2) < 0
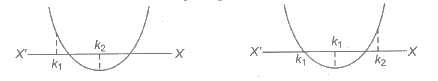
(vi) A given number k lies between the roots iff f(k) < O. In particular, the roots of the equation will be of opposite sign, iff 0 lies between the roots.
⇒ f(0) < 0
Wavy Curve Method
Let f(x) = (x – a1)k1 (x – a2)k2(x — a3)k3 … (x – an – 1)kn – 1 (x – an)kn
where k1, k2, k3,…, kn ∈ N and a1, a2, a3,…, an are fixed natural numbers satisfying the condition.
a1 < a2 < a3 < … < an – 1 < an..
First we mark the numbers a1, a2, a3,…, an on the real axis and the plus sign in the interval of the right of the largest of these numbers, i.e., on the right of an. If kn is even, we put plus sign on the left of an and if kn is odd, then we put minus sign on the left of an In the next interval we put a sign according to the following rule.
When passing through the point an – 1 the polynomial f(x) changes sign . if kn – 1 is an odd number and the polynomial f(x) has same sign if kn – 1 is an even number. Then, we consider the next interval and put a sign in it using the same rule.
Thus, we consider all the intervals. The solution of f(x) > 0 is the union of all interval in which we have put the plus sign and the solution of f(x) < 0 is the union of all intervals in which we have put the minus Sign.
Descarte’s Rule of Signs
The maximum number of positive real roots of a polynomial equation f(x) = 0 is the number of changes of sign from positive to negative and negative to positive in f(x) .
The maximum number of negative real roots of a polynomial equation f(x) = 0 is the number of changes of sign from positive to negative and negative to positive in f(x).
Rational Algebraic In equations
(i) Values of Rational Expression P(x)/Q(x) for Real Values of x, where P(x) and Q(x) are Quadratic Expressions To find the values attained by rational expression of the form a1x2 + b1x + c1 / a2x2 + b2x + c2
for real values of x.
(a) Equate the given rational expression to y.
(b) Obtain a quadratic equation in x by simplifying the expression,
(c) Obtain the discriminant of the quadratic equation.
(d) Put discriminant ≥ 0 and solve the in equation for y. The values of y so obtained determines the set of values attained by the given rational expression.
(ii) Solution of Rational Algebraic In equation If P(x) and Q(x) are polynomial in x, then the in equation P(x) / Q(x) > 0,
P(x) / Q(x) < 0, P(x) / Q(x) ≥ 0 and P(x) / Q(x) ≤ 0 are known as rational algebraic in equations.
To solve these in equations we use the sign method as
(a) Obtain P(x) and Q(x).
(b) Factorize P(x) and Q(x) into linear factors.
(c) Make the coefficient of x positive in all factors.
(d) Obtain critical points by equating all factors to zero.
(e) Plot the critical points on the number line. If these are n critical points, they divide the number line into (n + 1) regions.
(f) In the right most region the expression P(x) / Q(x) bears positive sign and in other region the expression bears positive and negative signs depending on the exponents of the factors .
Lagrange’s identity
If a1, a2, a3, b1, b2, b3 ≠ R, then
(a12 + a22 + a32) (b12 + b22 + b32) – (a1b1 + a2b2 + a3b3)2
= (a1b2 – a2b1)2 + (a2b3 – a3b2 )2 + (a3b1 – a1b3)2
Algebraic Interpretation of Rolle’s Theorem
Let f (x) be a polynomial having α and β as its roots such that α < β, f(α) = f(β) = 0.Also, a polynomial function is everywhere continuous and differentiable, then there exist θ ∈ (α, β) such that f'(θ) = 0. Algebraically, we can say between any two zeros of a polynomial f(x) there is always a derivative f’ (x) = 0.
Equation and In equation Containing Absolute Value
1. Equation Containing Absolute Value
By definition, |x| = x, if x ≥ 0 OR -x, if x < 0
If |f(x) + g(x)| = |f(x)| + g(x)|, then it is equivalent to the system f(x) . g(x) ≥ 0.
If |f(x) – g(x)| = |f(x)| – g(x)|, then it is equivalent to the system f(x) . g(x) ≤ 0.
2.In equation Containing Absolute Value
(i) |x| < a ⇒ – a < x < a (a > 0)
(ii) |x| ≤ a ⇒ – a ≤ x ≤ a
(iii) |x| > a ⇒ x < – a or x > a
(iv) |x| ≥ a ⇒ x le; – a or x ≥ a
3. Absolute Value of Real Number
|x| = -x, x < 0 OR +x, x ≥ 0
(i) |xy| = |x||y|
(ii) |x / y| = |x| / |y|
(iii) |x|2 = x2
(iv) |x| ≥ x
(v) |x + y| ≤ |x| + |y|
Equality hold when x and y same sign.
(vi) |x – y| ≥ ||x| – |y||
Inequalities
Let a and b be real numbers. If a – b is negative, we say that a is less than b (a < b) and if a – b is positive, then a is greater than b (a > b).
Important Points to be Remembered
(i) If a > b and b > c, then a > c. Generally, if a1 > a2, a2 > a3,…., an – 1 > an, then a1 > an.
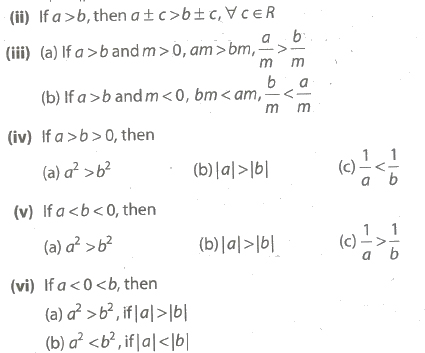
(vii) If a < x < b and a, b are positive real numbers then a2 < x2 < b2
Important Inequality
1. Arithmetico-Geometric and Harmonic Mean Inequality
(i) If a, b > 0 and a ≠ b, then
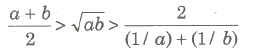
(ii) if ai > 0, where i = 1,2,3,…,n, then
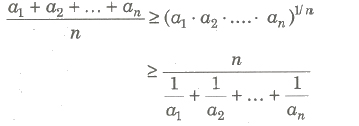
(iii) If a1, a2,…, an are n positive real numbers and m1, m2,…,mn are n positive rational numbers, then
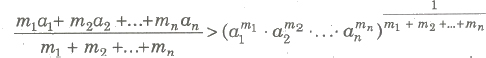
i.e., Weighted AM > Weighted GM
(iv) If a1, a2,…, an are n positive distinct real numbers, then
(a)
(b)
(c) If a1, a2,…, an and b1, b2,…, bn are rational numbers and M is a rational number, then
(d)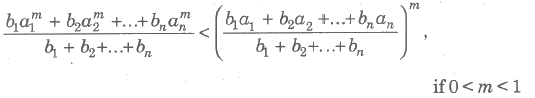
(v) If a1, a2, a3,…, an are distinct positive real numbers and p, ,q, r are natural numbers, then
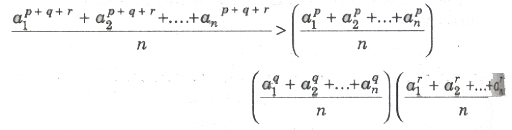
2. Cauchy – Schwartz’s inequality
If a1, a2,…, an and b1, b2,…, bn are real numbers, such that
(a1b1 + a2b2 + …+ anbn)2 ≤ (a12 + a22 + …, an2) * (b12 + b22 + …, bn2)
Equality holds, iff a1 / b1 = a2 / b2 = an / bn
3. Tchebychef’s Inequality
Let a1, a2,…, an and b1, b2,…, bn are real numbers, such that
(i) If a1 ≤ a2 ≤ a3 ≤… ≤ an and b1 ≤ b2 ≤ b3 ≤… ≤ bn, then
n(a1b1 + a2b2 + a3b3 + …+ anbn) ≥ (a1 + a2 + …+ an) (b1 + b2 + …+ bn)
(ii) If If a1 ≥ a2 ≥ a3 ≥… ≥ an and b1 ≥ b2 ≥ b3 ≥… ≥ bn, then
n(a1b1 + a2b2 + a3b3 + …+ anbn) ≤ (a1 + a2 + …+ an) (b1 + b2 + …+ bn)
4. Weierstrass Inequality
(i) If a1, a2,…, an are real positive numbers, then for n ≥ 2
(1 + a1)(1 + a2) … (1 + an) > 1 + a1 + a2 + … + an
(ii) If a1, a2,…, an are real positive numbers, then
(1 – a1)(1 – a2) … (1 – an) > 1 – a1 – a2 – … – an
5. Logarithm Inequality
(i) (a) When y > 1 and logy x > z ⇒ x > yz
(b) When y > 1 and logy x < z ⇒ 0 < x < yz
(ii) (a) When 0 < y < 1 and logy x > z ⇒ 0 < x < yz
(b) hen 0 < y < 1 and logy x < z ⇒ x > yz
Application of Inequalities to Find the Greatest and Least Values
(i) If xl,x2,…,xn are n positive variables such that xl + x2 +…+ xn = c (constant), then the product xl * x2 *….* xn is greatest when x1 = x2 =… =xn = c/n and the greatest value is (c/n)n.
(ii) If xl,x2,…,xn are positive variables such that xl,x2,…,xn = c (constant), then the sum xl+ x2 +….+ xn is least when x1 = x2 =… =xn = c1/n and the least value of the sum is n (c1/n).
(iii) If xl,x2,…,xn are variables and ml,m2,…,mn are positive real number such that xl + x2 +….+ xn = c (constant), then xlml * x2m2 *… * xnmn is greatest, when
xl / ml = x2 / m2 =…= xn / mn
= xl + x2 +….+ xn / ml + m2 +….+ mn
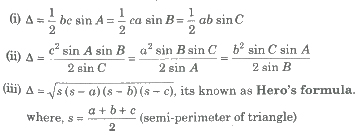
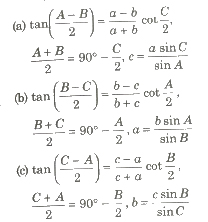
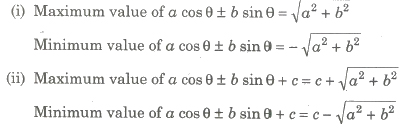
the beginning.
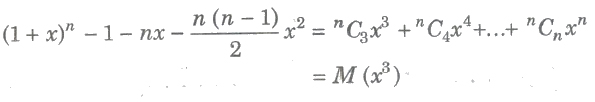
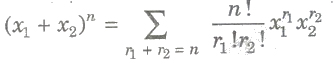
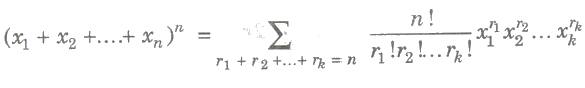
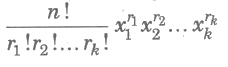
where q and r are the quotient and remainder respectively, when n is divided by m.
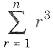and number of square of any size is
.
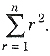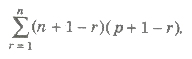
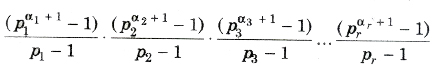
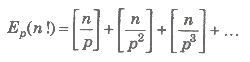
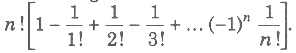
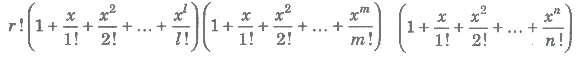
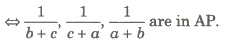
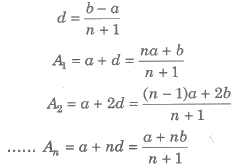
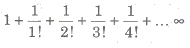number e.
