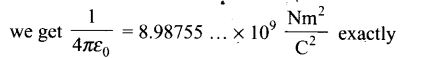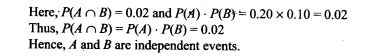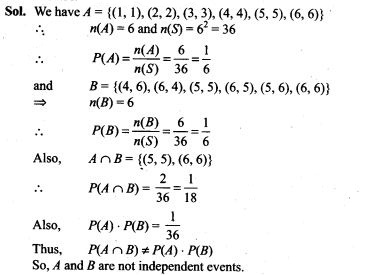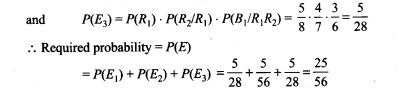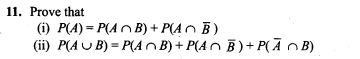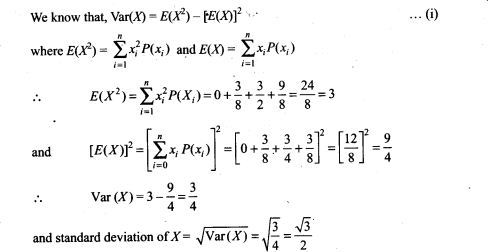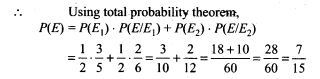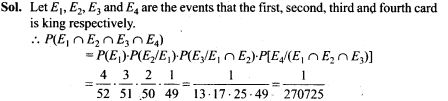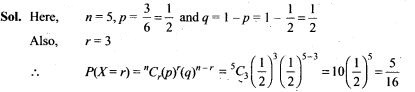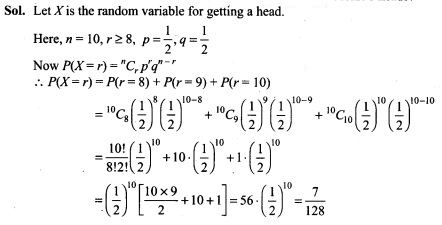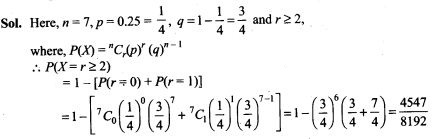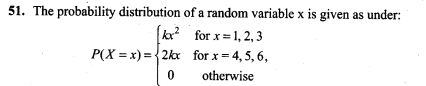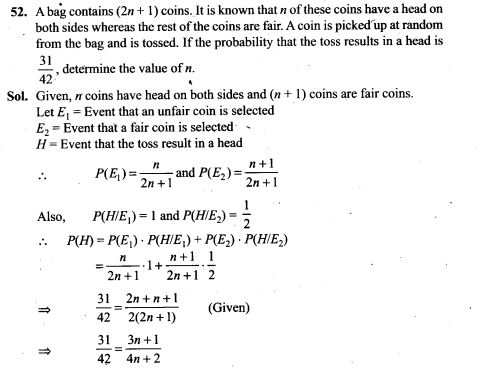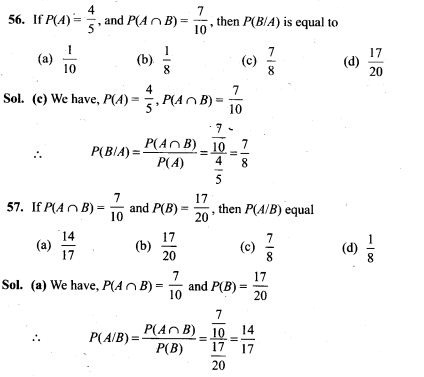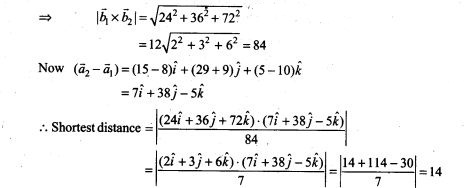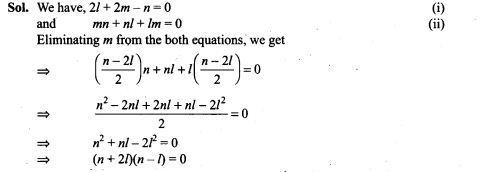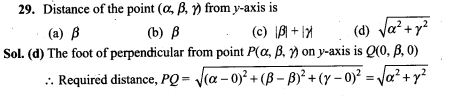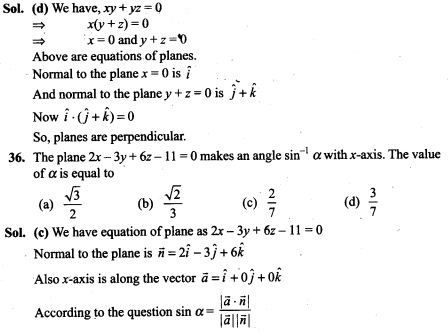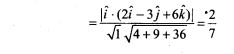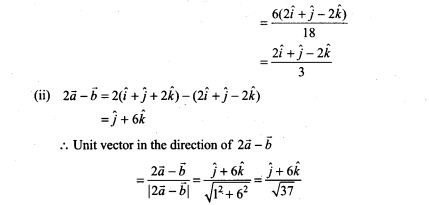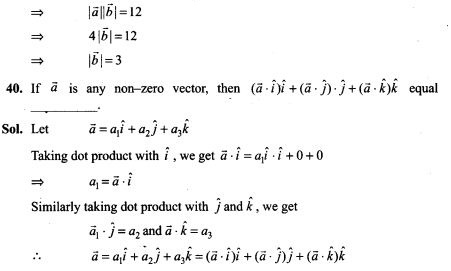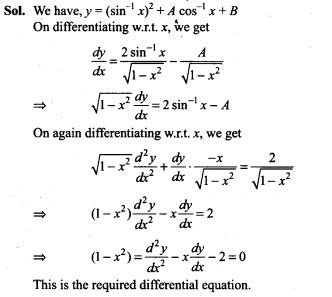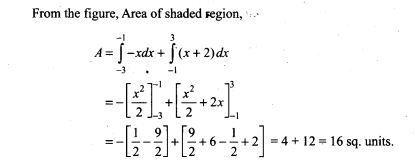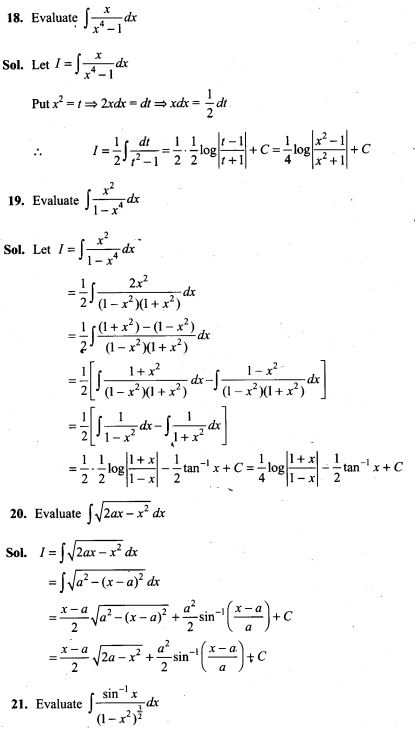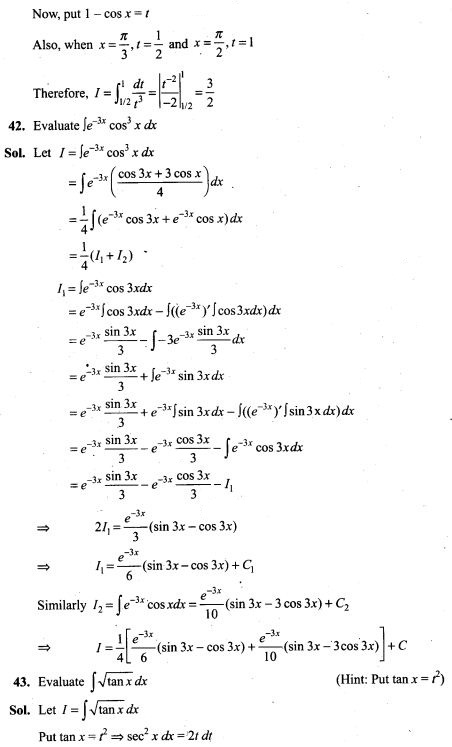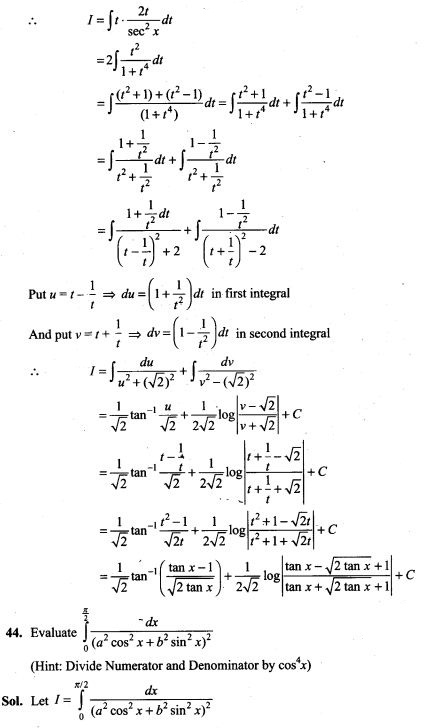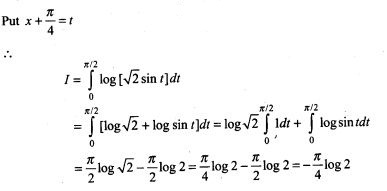Blog

Electrostatic Potential and Capacitance NCERT Exemplar Problems Solutions Physics

NCERT Exemplar Problems Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance

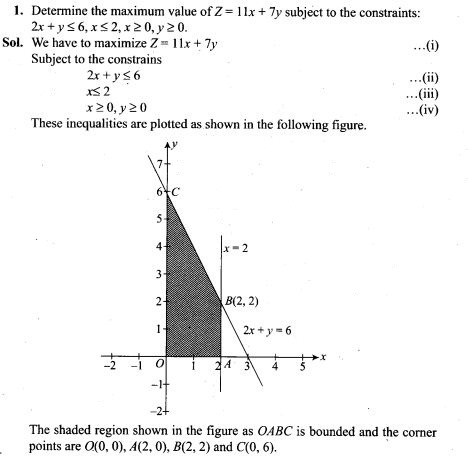
Multiple Choice Questions

Single Correct Answer Type
Question 1.

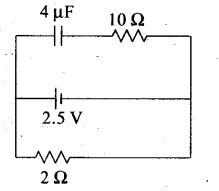
A capacitor of 4 μF is connected as shown in the circuit. The internal resistance of the battery is 0.5 Ω. The amount of charge on the capacitor plates will be
(a) 0 (b) 4 μC
(c) 16 μC (d) 8 μC
Solution: (d)
Key concept: A capacitor offers zero resistance in a circuit when it is uncharged, i.e., it can be assumed as short circuited and it offers infinite resistance when it is fully charged.

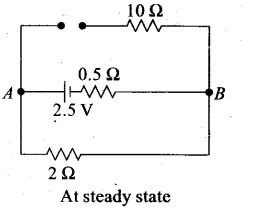
At steady state the capacitor offers infinite resistance in DC circuit and acts as open circuit as shown in figure, therefore no current flows through the capacitor and 10 Ω resistance, leaving zero potential difference across 10 Ω resistance. Hence potential difference across capacitor will be the potential difference across A and B.
The potential difference across lower and middle branch of circuit is equal to the potential difference across capacitor of upper branch of circuit.
Current flows through 2 Ω resistance from left to right, is given by I=v/R+r=1A.The potential difference across 2Ω resistance, V=IR= 1 x 2 = 2V Hence potential difference across capacitor is also 2 V.
The charge on capacitor is q = CV= (2 μF) x 2 V = 8 μC.

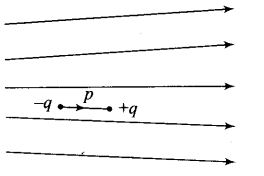
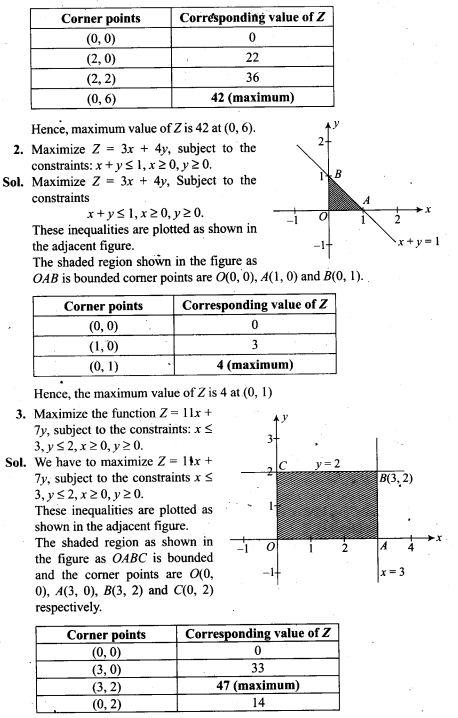
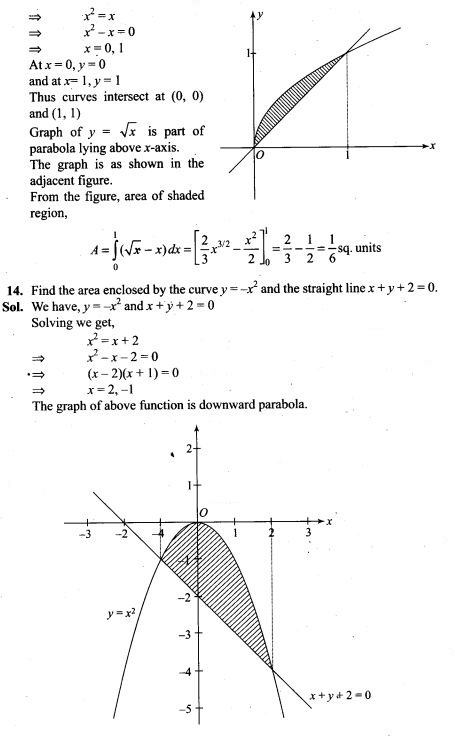
Question 2. A positively charged particle is released from rest in an uniform electric field. The electric potential energy of the charge
(a) remains a constant because the electric field is uniform
(b) increases because the charge moves along the electric field
(c) decreases because the charge moves along the electric field
(d) decreases because the charge moves opposite to the electric field
Solution: (c)
Key concept: Electric potential decreases in the direction of electric field. The direction of electric field is always perpendicular to one equipotential surface maintained at high electrostatic potential to other equipotential surface maintained at low electrostatic potential.
The positively charged particle experiences electrostatic force along the direction of electric field, hence moves in the direction of electric field. Thus, positive work is done by the electric field on the charge .We know

Hence electrostatic potential energy of the positive charge decreases.

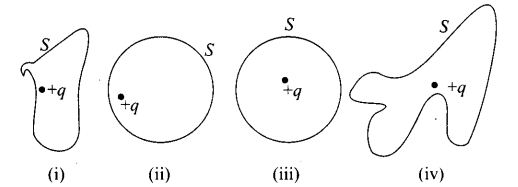
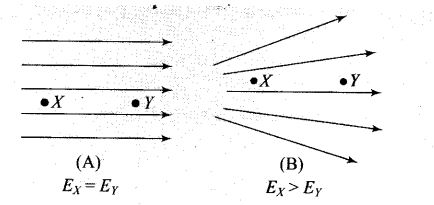
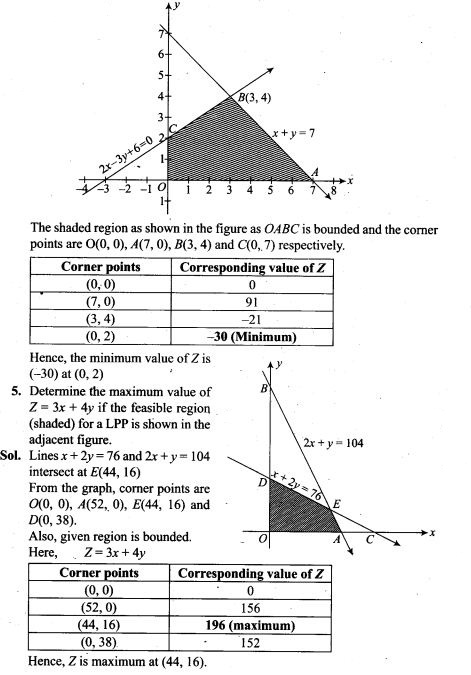
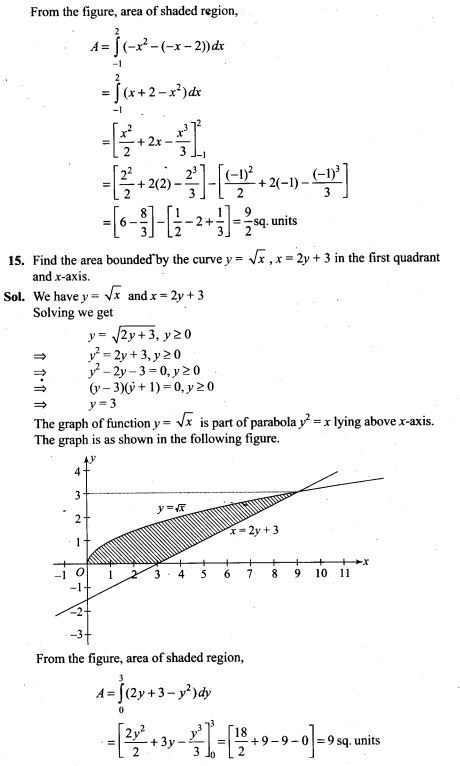
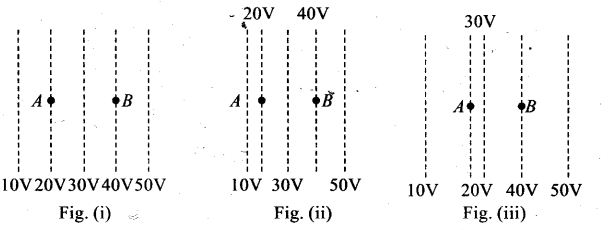
Question 3. Figure shows some equipotential lines distributed in space. A charged object is moved from point A to point B.
(a) The work done in Fig. (i) is the greatest.
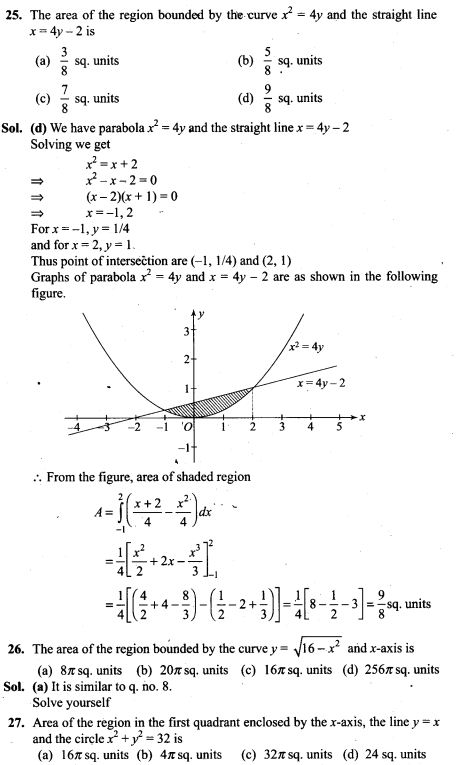
(b) The work done in Fig. (ii) is least.
(c) The work done is the same in Fig. (i), Fig.(ii) and Fig. (iii).
(d) The work done in Fig. (iii) is greater than Fig. (ii) but equal to that in

Solution: (c)
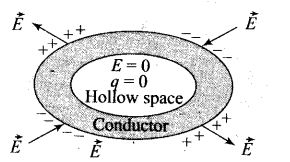
Key concept: For a given charge distribution, locus of all points or regions for which the electric potential has a constant value are called equipotential regions. Such equipotential can be surfaces, volumes or lines. Regarding equipotential surface the following points should be kept in mind:
• The density of the equipotential lines gives an idea about the magnitude of electric field. Higher the density, larger the field strength.
• The direction of electric field is perpendicular to the equipotential surfaces or lines.

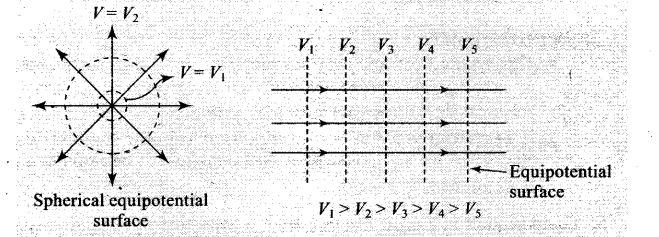
• The equipotential surfaces produced by a point charge or a spherically charge distribution are a family of concentric spheres.
• For a uniform electric field, the equipotential surfaces are a family of plane perpendicular to the field lines.
• A metallic surface ofany shape is an equipotential surface.
• Equipotential surfaces can never cross each other.
• The work done in moving a charge along an equipotential surface is always zero.
As the direction of electric field is always perpendicular to one equipotential surface maintained at high electrostatic potential than other equipotential surface maintained at low electrostatic potential. Hence direction of electric field is from B to A in all three cases.
The positively charged particle experiences electrostatic force along the direction of electric field, hence moves in the direction opposite to electric field. Thus, the work done by the electric field on the charge will be negative. We know

Here initial and final potentials are same in all three cases and same charge is moved, so work done is same in all three cases.

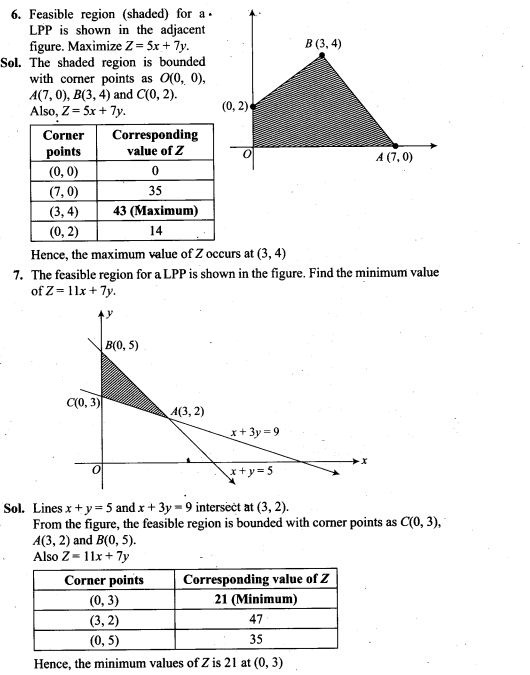
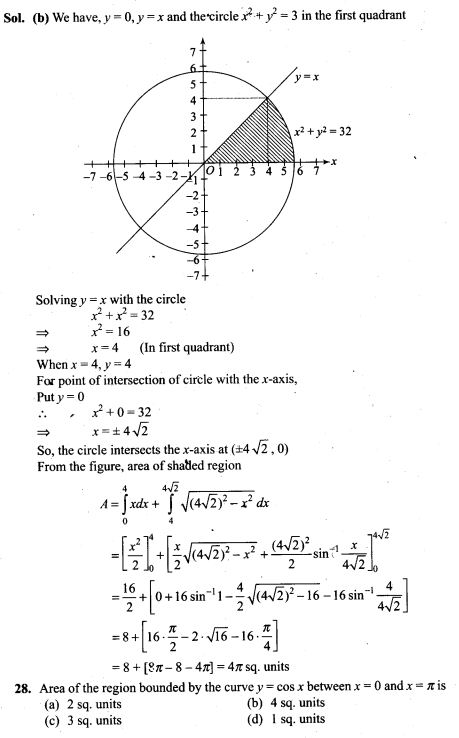
Question 4. The electrostatic potentiaLon the surface of a charged conducting sphere is 100 V. Two statements are made in this regard.
S₁: At any point inside the sphere, electric intensity is zero.
S₂: At any point inside the sphere, the electrostatic potential is 100 V.
Which of the following is a correct statement?
(a) S₁ is true but S₂ is false
(b) Both S₁ and S₂ are false
(c) S₁ is true, S₂ is also true and 5, is the cause of S₂
(d) S₂ is true, S₂ is also true but the statements are independent
Solution: (c) We know, the electric field intensity E and electric potential V are related
E=dV/dr
If electric field intensity E= 0, then dV/dr = 0. It means, E = 0 inside the charged conducting sphere causes uniform potential inside the sphere. Hence uniform electrostatic potential 100 V will be at any point inside the sphere.
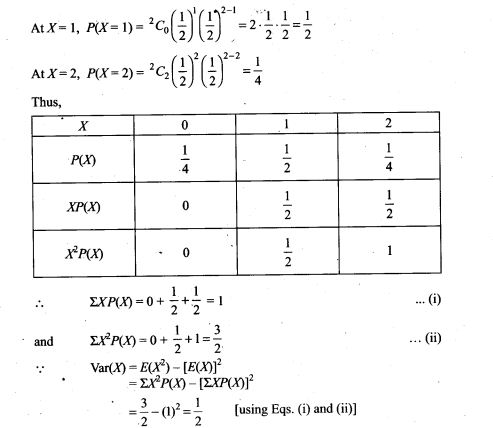
Important points:
• The electric field zero does not necessary imply that electric potential is zero. E.g., the electric field intensity at any point inside the charged spherical shell is zero but there may exist non-zero electric potential.
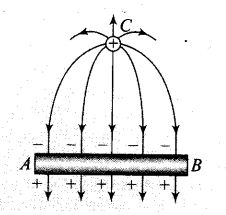
• If two charged particles of same magnitude but opposite sign are
placed, the electric potential at the midpoint will be zero but electric field is not equal to zero. *

Question 5. Equipotentials at a great distance from a collection of charges whose total sum is not zero are approximately
(a) spheres (b) planes
(c) paraboloids (d) ellipsoids
Solution: (a) The collection of charges, whose total sum is not zero, with regard to great distance can be considered as a single point charge. The equipotential surfaces due to a point charge are spherical.
Important point:
The electric potential due to point charge q is given by V=q/4πϵ₀r
It means electric potential due to point charge is same for all equidistant points. The locus of these equidistant points, which are at same potential, form spherical surface.

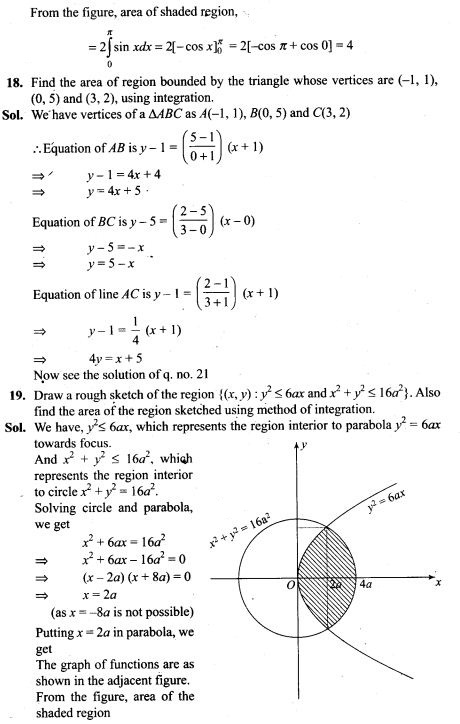
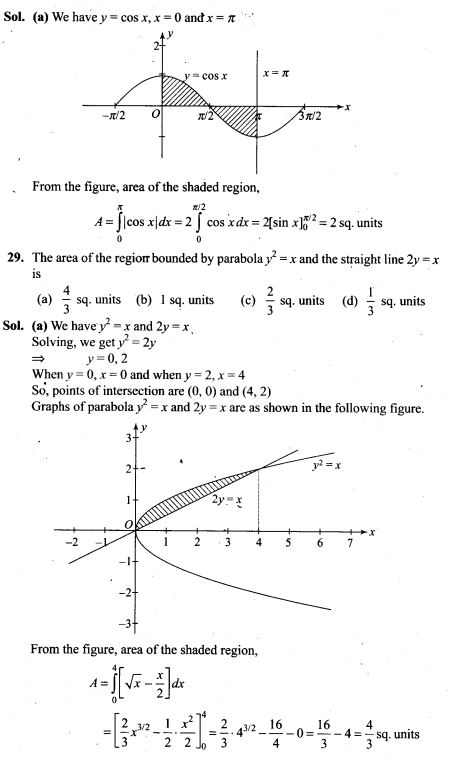
Question 6. A parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness d₁ and dielectric constant K₁ and the other has thickness d₂ and dielectric constant K₂ as shown in figure. This arrangement can be thought as a dielectric slab of thickness d (= d₁ + d₂) and effective dielectric constant K. Then K is

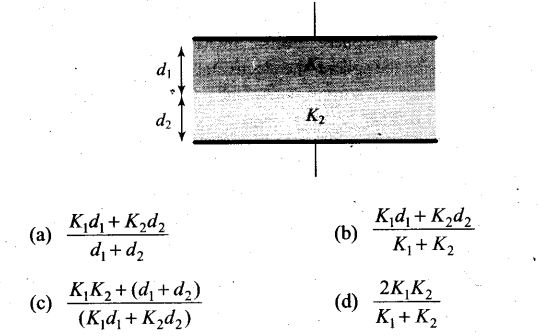
Solution: (c) Here the system can be considered as two capacitors C₁ and C₂ connected in series as shown in figure.

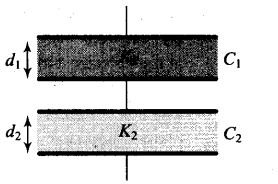
The capacitance of parallel plate capacitor filled with dielectric block has thickness d₁ and dielectric constant K₂ is given by

One or More Than One Correct Answer Type

Question 7. Consider a uniform electric field in the z -direction. The potential is a constant
(a) in all space (b) for any x for a given z
(c) for any y for a given z (d) on the x-y plane for a given z
Solution: (b c, d) We know, the electric field intensity E and electric potential V are

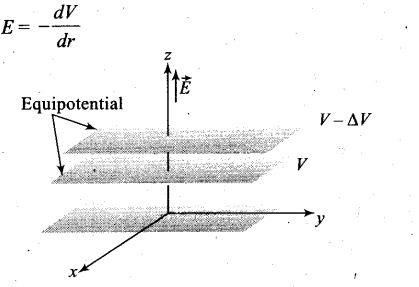
Electric potential decreases inf the direction of electric field. The direction of electric field is always perpendicular to one equipotential surface maintained at high electrostatic potential to other equipotential surface maintained at low electrostatic potential.
The electric field in z-direction suggest that equipotential surfaces are in x-y plane. Therefore the potential is a constant for any x for a given z, for any y for a given z and on the x-y plane for a given z.

Question 8. Equipotential surfaces
(a) are closer in regions of large electric fields compared to regions of lower electric fields
(b) will be more crowded near sharp edges of a conductor
(c) will be more crowded near regions of large charge densities
(d) will always be equally spaced
Solution: (a, b, c)
Key concept: The density of the equipotential lines gives an idea about the magnitude of electric field. Higher the density, larger the field strength.
We know, the electric field intensity E and electric potential V are related as

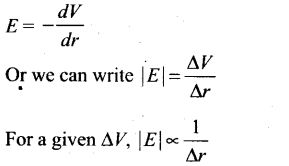
Hence the electric field intensity E is inversely proportional to the separation between equipotential surfaces. So, equipotential surfaces are closer in regions of large electric fields.
As electric field intensities is large near sharp edges of charged conductor and near regions of large charge densities. Therefore, equipotential surfaces are closer at such places.

Question 9. The work done to move a charge along an equipotential from A to B

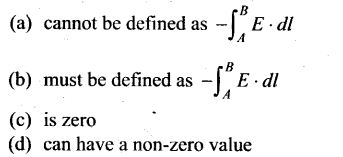
Solution: (b, c)
Key concept: The work done by the external agent in shifting the test charge along the dashed line from 1 to 2 is

Question 10. In a region of constant potential
(a) the electric field is uniform
(b) the electric field is zero
(c) there can be no charge inside the region
(d) the electric field shall necessarily change if a charge is placed outside the region
Solution: (b, c) We know, the electric field intensity E and electric potential V are dV
related as E =- dV/dr
or we can write |E|=ΔV/Δr
The electric field intensity E and electric potential V are related as E = 0 and for V = constant,dV/dr=0 this imply that electric field intensity E = 0.
If some charge is present inside the region then electric field cannot be zero at that region, for this V = constant is not valid.

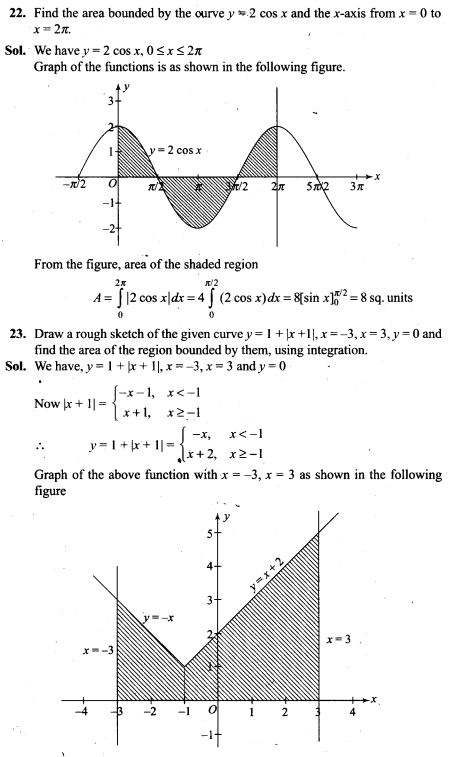
Question 11.

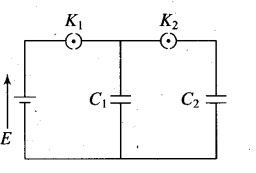
In the circuit shown in figure initially key K₁
is closed and key K₂ is open. Then K₁ is opened and K₂ is closed (order is important).
[Take Q’₁ and Q’₂ as charges on C₁ and C₂ and V₁ and V₂ as voltage respectively.]
Then, E
(a) charge on C, gets redistributed such that V₁ = V₂
(b) charge on C₁ gets redistributed such that Q’₁ = Q’₂
(c) charge on C₁ gets redistributed such that C₁V₁ + C₂V₂ = C₁E
(d) charge on C₁ gets redistributed such that Q’₁ + Q’₂=Q
Solution: (a, d) Initially key K₁ is closed and key K₂ is open, the capacitor C₁ is charged by battery and capacitor C₂ is still uncharged. Now K₁ is opened and K₂ is closed, the capacitors C₁ and C₂ both are connected in parallel. The charge stored by capacitor C₁, gets redistributed between C₁ and C₂ till their potentials become same, i.e., V₂ = V₁.
By law of conservation of charge, the charge stored in capacitor Cx is equal to sum of charges on capacitors C₁ and C₂ when K₁ is opened and K₂ is closed, i.e.,
Q’₁+Q’₂=Q

Question 12. If a conductor has a potential V≠0 and there are no charges anywhere else outside, then
(a) there must be charges on the surface or inside itself
(b) there cannot be any charge in the body of the conductor
(c) there must be charges only on the surface
(d) there must be charges inside the surface
Solution: (a, b) The potential of a body is due to charge of the body and due to the charge of surrounding. If tfiere are no charges anywhere else outside, then the potential of the body will be due to its own charge. If there is a cavity inside a conducting body, then charge can be placed inside the body. Hence there must be charges on its surface or inside itself. Hence option (a) is correct. The charge resides on the outer surface of a closed charged conductor. Hence there cannot be any charge in the body of the conductor. Hence option (b) is correct.

Question 13.

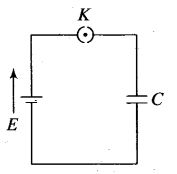
A parallel plate capacitor is connected to a battery as shown in figure. Consider two situations.
A. Key K is kept closed and plates of capacitors are moved apart using insulating handle.
B. Key K is opened and plates of capacitors are moved apart using insulating handle.
Choose the correct option(s).
(a) In A, Q remains the same but G changes
(b) In B, V remains the same but C changes
(c) In A, V remains the same hence Q changes
(d) In B ,Q remains the same hence V changes
Solution: (c, d) The battery maintains the potential difference across connected capacitor in every circumstance. However, charge stored by disconnected charged capacitor remains conserved.
Case A: When key K is kept closed and plates of capacitors are moved apart using insulating handle.
The battery maintains the potential difference across connected capacitor in every circumstance. The separation between two plates increases which in turn decreases its capacitance (C=ϵ₀A/d)and potential difference across
connected capacitor continue to be the same as capacitor is still connected with battery. Hence, the charge stored decreases as Q = CV.
Case B: When key K is opened and plates of capacitors are moved apart using insulating handle.
The charge stored by isolated charged capacitor remains conserved. The separation between two plates is increasing which in turn decreases its capacitance with the decrease of capacitance, potential difference V increases as V=Q/C.

Very Short Answer Type Questions

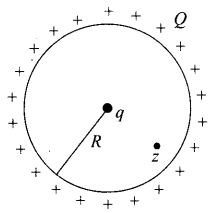
Question 14. Consider two conducting spheres of radii R₁ and R₂ with R₁ > R₂. If the two are at the same potential, the larger sphere has more charge than the smaller sphere. State whether the charge density of the smaller sphere is more or less than that of the larger one.
Solution: Since, the two spheres are at the same potential, therefore

Question 15. Do free electrons travel to region of higher potential or lower potential?
Solution: The force on a charge particle in electric field F = qE
The free electrons (negative charge) experience electrostatic force in a direction opposite to the direction of electric field.
Thedirection of electric field is always from higher potential tolower. Hence direction of travel of electrons is from lower potential to region of higher potential.

Question 16. Can there be a potential difference between two adjacent conductors carrying the same charge?
Solution: Yes, if the sizes are different.
Explanation: We define capacitance of a conductor C = Q/V is the charge
of conductor and V is the potential of the conductor. For given charge potential V ∝ 1/C. The capacity of conductor depends on its geometry, so two adjacent conductors carrying the same charge of different dimensions may have different potentials.

Question 17. Can the potential function have a maximum or minimum in free space?
Solution: No, the potential function does not have a maximum or minimum in free
space, it is because the absence of atmosphere around conductor prevents the phenomenon of electric discharge or potential leakage.

Question 18.

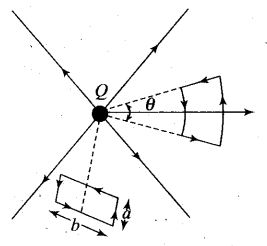
A test charge q is made to move in the electric field of a point charge Q along two different closed paths [figure first path has sections along and perpendicular to lines of electric field]. Second path is a rectangular loop of the same area as the first loop. How does the work done compare in the two cases?
Solution: Work done will be zero in both the cases.
Explanation: The electrostatic field is conservative, and in this field work done by electric force on the charge in a closed loop is zero. In this question both are closed paths, hence the work done in both the cases will be zero.

Short Answer Type Questions

Question 19. Prove that a closed equipptential surface with no charge within itself must enclose an equipotential volume.
Solution: Let us assume that in a closed equipotential surface with no charge the potential is changing from position to position. Let the potential just inside the surface is different to that of the surface causing in a potential gradient (dV/dr)
It means E ≠ 0 electric field comes into existence, which is given by as E=-dV/dr
It means there will be field lines pointing inwards or outwards from the surface. These lines cannot be again on the surface, as the surface is equipotential. It is possible only when the other end of the field lines are originated from the charges inside. This contradicts the original assumption. Hence, the entire volume inside must be equipotential.

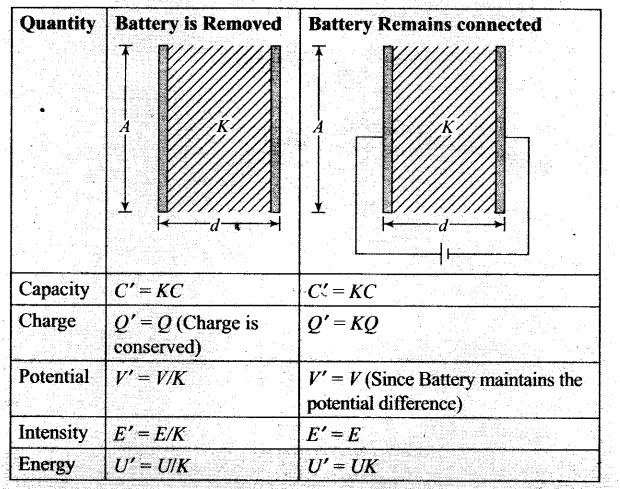
Question 20. A capacitor has some dielectric between its plates and the capacitor is connected to a DC source. The battery is now disconnected and then the dielectric is removed. State whether the capacitance, the energy stored in it, electric field, charge stored and the voltage will increase, decrease or remain constant.
Solution: The capacitance of the parallel plate capacitor, filled with dielectric medium of dielectric constant K is given by C=K ϵ₀A/d
The capacitance of the parallel plate capacitor decreases with the removal of dielectric medium as for air or vacuum K = 1 and for dielectric K > 1.
If we disconnect the battery from capacitor, then the charge stored will remain the same due to conservation of charge.
The energy stored in an isolated charge capacitor U =q²/2C as q is constant, energy stored U ∝ 1/C .As C decreases with the removal of dielectric medium, therefore energy stored increases.
The potential difference across the plates of the capacitor is given by V =q/C
Since q is constant and C decreases which in turn increases V and therefore E increases as E = V/d.
Important point:

Question 21. Prove that, if an insulated, uncharged conductor is placed near a charged conductor and no other conductors are present, the uncharged body must intermediate in potential between that of the charged body and that of infinity.
Solution: The electric field E = dV/dr suggests that electric potential decreases along the direction of electric field.
Let us take any path from the eharged’conductor to the uncharged conductor along the direction of electric field. Therefore, the electric potential decrease along this path.
Now, another path from the uncharged conductor to infinity will again continually lower the potential further. This ensures that the uncharged body must be intermediate in potential between that of the charged body and that of infinity.

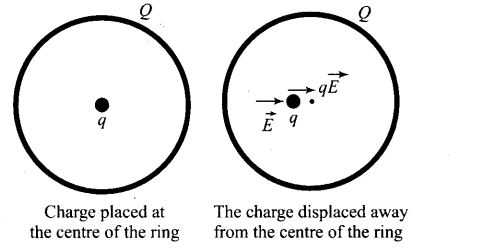
Question 22. Calculate potential energy of a point charge -q placed along the axis due to a charge +Q uniformly distributed along a ring of radius R. Sketch PE, as a function of axial distance z from the centre of the ring. Looking at graph, can you see what would happen if -q is displaced slightly from the centre of the ring (along the axis)?
Solution: The potential energy (U) of a point charge q placed at-potential V,U=qV In our case a negative charged particle is placed at the axis of a ring having charge Q. Let the ring has radius a,the electric potential at an axial distance z from the centre of the ring is

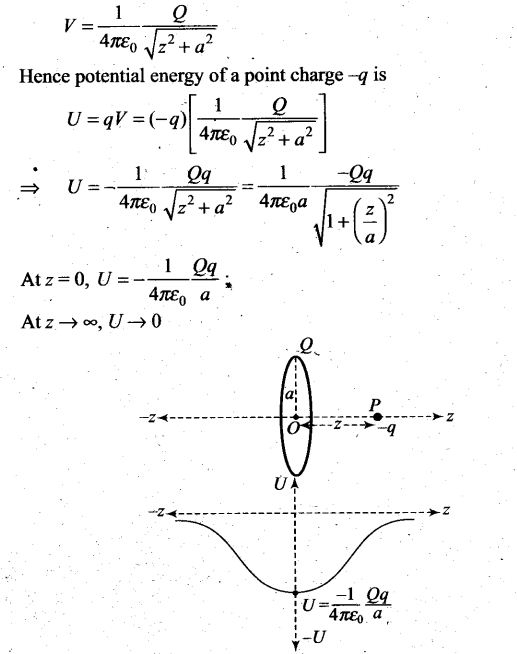
The variation of potential energy with z is shown in the figure.
The charge -q displaced would perform oscillations. Nothing can be concluded just by looking at the graph.

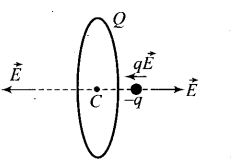
Question 23. Calculate the potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.
Solution:

Long Answer Type Questions

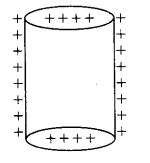
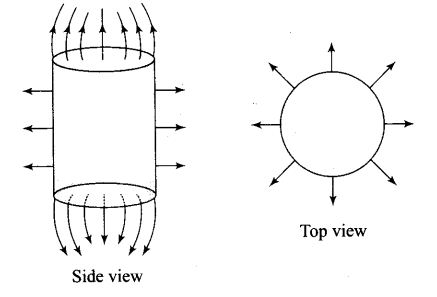
Question 24. Find the equation of the equipotentials for an infinite cylinder of radius r0 carrying charge of linear density A.
Solution: We know the integral relation between electric field gives potential difference between two points.
The electric field due to line charge need to be obtained in order to find the potential at distance r from the line chaige. For this we need to apply Gauss’ theorem.
Let the field lines must be radically outward. Draw a cylindrical Gaussian surface of radius r and length l.

>

Question 25. Two point charges of magnitude +q and -q are placed at (-d/2, 0, 0) and (d/2, 2, 0), respectively. Find the equation of the equipotential surface where the potential is zero.
Solution: Let the required plane lies at a distance x from the origin as shown in figure.

Question 26. A parallel plate capacitor is filled by a dielectric whose relative permittivity varies with the applied voltage (U) as ε= αU where α = 2V^-1. A similar capacitor with no dielectric is charged to U₀ = 78 V. It is then connected to the uncharged capacitor with the dielectric. Find the final voltage on the capacitors.
Solution: Both capacitors will be connected in parallel, hence the potential difference across both capacitors should be same. Assuming the required final voltage. be U. If C is the capacitance of the capacitor without the dielectric, then the charge on the capacitor is given by Q₁ = CU.
As the capacitor with the dielectric has a capacitance εC. Hence, the charge on the capacitor is given by

Question 27. A capacitor is made of two circular plates of radius R each, separated by a , distance d << R. The capacitor is connected to a constant voltage. A thin
conducting disc of radius r << R and thickness t << r is placed at the centre of the bottom plate. Find the minimum voltage required to lift the disc if the mass of the disc is m.
Solution: Initially the thin conducting’disc is placed at the centre of the bottom plate, the potential of the disc will be equal to potential of the disc. The disc will be lifted if weight is balanced by electrostatic force.
The electric field on the disc, when potential difference V is applied across it

Question 28. (a) In a quark model of elementary particles, a neutron is made of one up quarks [charge (2/3)e] and two down quarks [charges (-l/3)e]. Assume that they have a triangle configuration with side length of the order of 10^-15m. Calculate electrostatic potential energy of neutron and compare it with its mass 939 MeV.
(b) Repeat above exercise for a proton which is made of two up and one down quark.
Solution: This system is made up of three charges. The potential energy of the system is equal to the algebraic sum of PE of each pair. So,

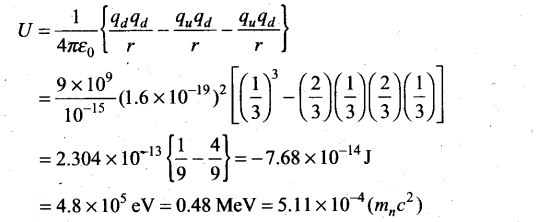
Question 29. Two metal spheres, one of radius R and the other of radius 2R, both have same surface charge density σ. They are brought in contact and separated. What will be the new surface charge densities on them?
Solution: The charges on metal spheres before contact, are

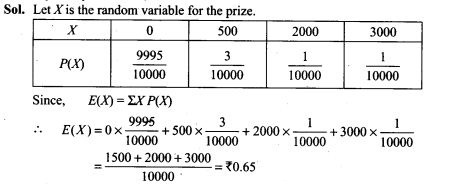
Question 30. In the circuit shown in figure, initially K₁ is closed and K₂ is open. What are the charges on each capacitors?
Then K₁ was opened and K₂ was closed (order is important), what will be the charge on each capacitor now? [C = 1 μF]

Solution: In the circuit, when initially K₁ is closed and K₂ is open, the capacitors C₁ and C₂ connected in series with battery acquire equal charge.

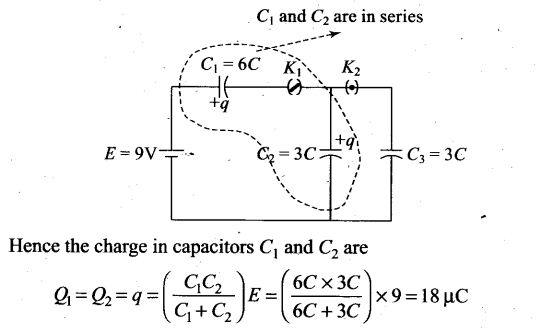
Hence the charge in capacitors C₁ and C₂ are
Henee Q₁ = Q₂ = 18 μC and Q₃ = 0
Now K₁ was opened and K₂ was closed, the battery and capacitor C, are disconnected from the circuit .The charge in capacitor C, will remain constant equal to Q₁ – Q₂ = 18 μC . The charged capacitor C₂ now connects in parallel with uncharged capacitor C₃, considering common potential of parallel combination as V.

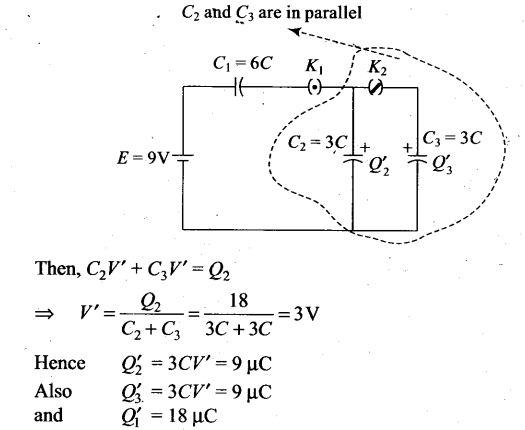
Question 31. Calculate potential on the axis of a disc of radius R due to a charge Q
uniformly distributed on its surface.
Solution:

Question 32. Two charges q₁ and q₂ are placed at (0, 0, d) and (0, 0, -d) respectively. Find
the locus of points where the potential is zero.
Solution:
Key concept: Following the principle of superposition of potentials as
described in last section, let us find the potential V due to a collection of
discrete point charges q₁, q₂, …,q_n, at a point P.

Question 33.

Solution:

March 20, 2018
Electric Charges and Fields NCERT Exemplar Problems Solutions Physics

NCERT Exemplar Problems Class 12 Physics Chapter 1 Electric Charges and Fields

Multiple Choice Questions

Single Correct Answer Type
Question 1. In figure two positive charges q₂ and q₃ fixed along the y-axis, exert a net electric force in the +x-direction on a charge q₁, fixed along the x-axis. If a positive charge Q is added at (x, 0), the force on q₁

(a) shall increase along the positive x-axis
(b) shall decrease along the positive x-axis
(c) shall point along the negative x-axis
(d) shall increase but the direction changes because of the intersection of Q with q₂ and q₃
Solution: (a)
Key concept: Total force acting on a given charge due to the number of charges is the vector sum of the individual forces acting on that charge due

We know that like charges repel and unlike charges attract. The net electrostatic force on the charge qx by the charges q₂ and q₃ is along the positive x-direction. Hence the nature of force between q₁,q₂ and q₁, q₃ should be attractive. It means qx should be negative. This can be represented by the figure given alongside:
Now a positive charge Q is placed at (x, 0), hence the nature of force between q₁ and Q (positive) will be attractive and the force on q₁ by the charge Q should be along positive x-axis direction. Now we can say that net force on the charge qx due to charges q₂, q₃ and Q should be along the same direction as given in the diagram alongside:
Now it is clear from the figure given above that the force on qx shall increase along the positive x-axis due to the presence of positive charge Q placed at (x, 0).

Question 2. A point positive charge is brought near an isolated conducting sphere (figure). The electric field is best given by

Solution: (a)
Key concept:
• Electric field lines come out of positive charge and go into the negative charge.
• Tangent to the field line at any point gives the direction of the field at that point.
• Field lines are always normal to the conducting surface.
• Field lines do not exist inside a conductor.
The explanation to this problem-can be done by keeping two things in mind.
(i) Concept of induction
(ii) The electric field lines interact with a conducting body normally.
Let us discuss the phenomenon of induction involved in this case. When a positive point charge is brought near an isolated conducting sphere without touching the sphere, then the free electrons in the sphere are attracted towards the positive charge. Thus, the left surface of sphere has an excess of negative charge and the right surface of sphere has an excess of positive charge. It should be noted that both kinds of charges are bound in the metal sphere and cannot escape. They, therefore, reside on the surface of the sphere.

An electric field lines start from a positive point charge and ends at negative charge induced on the left surface of sphere. Also, electric field line emerges from a positive charge, in case of single charge and ends at infinity.
Here, all these conditions are fulfilled in Fig. (i).

Question 3. The electric flux through the surface

(a) in Fig. (iv) is the largest
(b) in Fig. (iii) is the least
(c) in Fig. (ii) is same as Fig. (iii) but is smaller than Fig. (iv)
(d) is the same for all the figures
Solution: (d)
Key concept: According to Gauss’ law of electrostatics, the total electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity,

Thus, electric flux through a surface doesn’t depend on the shape, size or area of a surface but it depends on the amount of charge enclosed by the surface.
In given figures the charge enclosed are same that means the electric flux through all the surfaces should be the same. Hence option (d) is correct.

Question 4. Five charges q₁, q₂, q₃, q₄ and q₅ are fixed at their positions as shown in
figure, S is a Gaussian surface. The Gauss’ law is given by

Which of the following statements is correct?
(a) E on the LHS of the above equation will have a contribution from q₁,q₅ and q₁, q₅ and q₃ while q on the RHS will have a contribution from q₁ and q₄ only

(b) E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q₂ and q₄ only
(c) E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q_1, q₃ and q₅ only
(d) Both E on the LHS and q on the RHS will have contributions from q₂ and q₄ only
Solution: (b)
Key concept: According to Gauss’ law, the term q_enclosed on the right side of the equation Ф_s E . dS =q_enclosed/ ϵ₀includes the sum of all charges enclosed by the surface called (Gaussian surface).
In left side equation, the electric field is due to all the charges present both inside as well as outside the Gaussian surface.
Hence in given question, E on LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q₂ and q₄ only. Hence option (b) is correct.

Question 5. Figure shows electric field lines in which an electric dipole P is placed as shown. Which of the following statements is correct?

(a) The dipole will not experience any force
(b)The dipole will experience a force towards right
(c)The dipole will experience a force towards left
(d)The dipole will experience a force upwards
Solution: (c)
Key concept: If the lines of forces are equidistant and parallel straight lines, the field is uniform and if either lines of force are not equidistant, or straight line or both, the field will be non-uniform. The number of electric field lmes passing per unit area is proportional to the strength of electric field. For example, see the following figures:

Hence in given question, from given pattern of electric field lines it is clear that the strength of electric field decreases from left to right. As a result force on charges also decreases from left to right.
Here in given figure, the force on charge -q is greater than force on charge +q in turn dipole will experience a force towards left. Hence option (c) is correct.

Question 6. A point charge +q is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of the plane is
(a) directed perpendicular to the plane and away from the plane
(b) directed perpendicular to the plane but towards the plane
(c) directed radially away from the point charge
(d) directed radially towards the point charge
Solution: (a) If a point positive charge is placed near an isolated conducting plane, free electrons are attracted towards the positive charge. Result of this some negative charge develops on the surface of the plane towards the positive charge side and an equal positive charge develops on opposite side of the plane. The electric field lines are away from positive charge and perpendicular to the surface. Hence the field at a point P on the other side of the plane is directed perpendicular to the plane and away from the plane, hence option (a) is correct.

Question 7. A hemisphere is uniformly charged positively. The electric field at a point on a diameter away from the centre is directed .
(a) perpendicular to the diameter

(b) parallel to the diameter
(c) at an angle tilted towards the diameter
(d) at an angle tilted away from the diameter
Solution: (a) In case of a uniformly positive charged hemisphere, if a point situated at a point on a diameter away from the centre, the electric field should be perpendicular to the diameter. In this case the component of electric field intensity parallel to the diameter cancel out.

One or More than One Correct Answer Type

Question 8. If Ф_s E . dS = 0 over a surface, then
(a) the electric field inside the surface and on it is zero
(b) the electric field inside the surface is necessarily uniform
(c) the number of flux lines entering the surface must be equal to the number of flux lines leaving it
(d) all charges must necessarily be outside the surface
Solution: (c, d)
Key concept: We know electric flux is proportional to the number of electric field lines and the term Ф_s E . dS represents electric flux over the closed surface.
It means Ф_s E . dS represents the algebraic sum of number of flux lines entering the surface and number of flux lines leaving the surface.
If Ф_s E . dS = 0, this means the number of flux lines entering the surface must be equal to the number of flux lines leaving from it.
From Gauss’ law, we know Ф_s E . dS = q/ ϵ₀ , here q is the charge enclosed by , the closed surface. If Ф_s E . dS = 0 then q = 0, i.e., net charge enclosed by the surface must be zero.
Hence all other charges must necessarily be outside the surface. This is because of the fact that charges outside the surface do not contribute to the electric flux.

Question 9. The electric field at a point is
(a) always continuous
(b) continuous if there is no charge at that point
(c) discontinuous only if there is a negative charge at that point
(d) discontinuous if there is a charge at that point
Solution: (b, d) We cannot define electric field at the position of a charge, so we cannot say that electric field is always continuous. Hence option (a) is ruled out and option (d) is the correct choice. The electric field due to any charge will be continuous, if there is no other charge in the medium. It will be discontinuous if there is a charge at the point under consideration, hence option (b) is correct.

Question 10. If there were only one type of charge in the universe, then

Solution: (b, d) From Gauss’ law, we know Ф_s E . dS =q/ ϵ₀, here q is the charge
enclosed by the closed surface. If Ф_s E . dS= 0 then q = 0, i.e., net charge
enclosed by the surface must be zero.
If the charge is outside the surface, then charge enclosed by the surface is q = 0 and thus, (j) Ф_s E . dS = 0 . Hence options (b) and (d) are correct.

Question 11. Consider a region inside which there are various types of charges but the total charge is zero. At points outside the region,
(a) the electric field is necessarily zero
(b) the electric field is due to the dipole moment of the charge distribution only j
(c) the dominant electric field is ∝ 1/r³, for large r, where r is the distance from an origin in this regions r
(d) the work done to move a charged particle along a closed path, away from the region, will be zero
Solution: (c, d) From Gauss’ law, we know Ф_s E . dS =q_enclosed/ ϵ₀. in left side equation.
the electric field is due to all the charges present both inside as well as outside the Gaussian surface. Hence if q_enclosed= 0, it cannot be said that the electric field is necessarily zero. .
If there are various types of charges in a region and total charge is zero, the region may be supposed to contain a number of electric dipoles.
Therefore, at points outside the region (may be anywhere w.r.t. electric
dipoles), the dominant electric field ∝ 1/r³ for large r.
The electric field is conservative, work done to move a charged particle along a closed path, away from the region will be zero.

Question 12. Refer to the arrangement of charges in figure and a Gaussian surface of radius R with Q at the centre. Then,

Solution:

The charge 5 Q lies outside the surface, thus it makes no contribution to electric flux through the given surface. Hence options (a) and (c) are correct.

Question 13. A positive charge Q is uniformly distributed along a circular ring of radius R. A small test charge q is placed at the centre of the ring figure. Then,

(a) if q > 0 and is displaced away from the centre in the plane of the ring, it will be pushed back towards the centre
(b) if q < 0 and is displaced away from the centre in the plane of the ring, it will never return to the centre and will continue moving till it hits the ring
(c) if q < 0, it will perform SHM for small displacement along the axis
(d) q at the centre of the ring is in an unstable equilibrium within the plane of the ring for q > 0
Solution: (a, b, c, d) The positive charge Q is uniformly distributed along the circular ring then electric field at the centre of ring will be zero, hence no force is experienced by the charge if it is placed at the centre of the ring.
Now the charge is displaced away from the centre in the plane of the ring. There will be net electric field opposite to displacement will push back the charge towards the centre of the ring if the charge is positive. If charge is negative, it will experience net force in the direction of displacement and the charge will continue moving till it hits the ring. Also this negative charge is in an unstable equilibrium. Hence options (a), (b) and (d) are correct.

The direction of electric field on the axis of a positively charged ring is along the axis of the ring and away from the centre of ring. If a negative charge is shifted away from the centre along the axis of ring, charge will experience a net force towards the centre and return to the centre and will perform SHM for small displacement along the axis.

Very Short Answer Type Questions

Question 14. An arbitrary surface encloses a dipole. What is the electric flux through this surface?
Solution: Zero.

Question 15. A metallic spherical shell has an inner radius R₁ and outer radius R₂. A charge Q is placed at the centre of the spherical cavity. What will be the surface charge density on .
(i) the inner surface (ii) the outer surface?
Solution: A charge Q is placed at the centre of the spherical cavity. So, the charge induced at the inner surface of the sphere will be -Q and at outer surface of the sphere is +Q.

Question 16. The dimensions of an atom are of the order of an Angstrom. Thus, there must be large electric fields between the protons and electrons. Why then is the electrostatic field inside a conductor zero?
Solution: In any neutral atom, the number of electrons and protons are equal, and the protons and electrons are bound into an atom with distinct and independent existence. Electrostatic fields are caused by the presence of excess charges. But there can be no excess charge on the intersurface of an isolated conductor. So, the electrostatic fields inside a conductor is zero despite the fact that the dimensions of an atom are of the order of an Angstrom.

Question 17. If the total charge enclosed by a Surface is zero, does it imply that the electric field everywhere on the surface is zero? Conversely, if the electric field everywhere on a surface is zero, does it imply that net charge inside is zero?
Solution: According to Gauss’ law, the flux associated with any closed surface is given
by Ф_s E . dS =q_enclosed /ϵ₀. The term q_enclosed on the right side of the equation includes the sum of all charges enclosed by the surface called (Gaussian surface).
In left side equation,the electric field is due to all the charges present both inside as well as outside the Gaussian surface.
Thus, despite being total charge enclosed by a surface zero, it doesn’t imply that the electric field everywhere on the surface is zero, the field may be normal to the surface.
Also, conversely if the electric field everywhere on a surface is zero.

Question 18. Sketch the electric field lines for a uniformly charged hollow cylinder shown in figure.

Solution: The electric field lines starts from positive charges and move towards infinity and meet plane surface normally as shown in the figure below:

Important point: No electric field lines will be present inside the cylinder because of electrostatic shielding. Electrostatic shielding/screening is the phenomenon of protecting a certain region of space from external electric field. Sensitive instruments and appliances are affected seriously with strong external electrostatic fields. Their working suffers and they may start misbehaving under the effect of unwanted fields.

The electrostatic shielding can be achieved by protecting and enclosing the sensitive instruments inside a hollow conductor because inside hollow conductors, electric fields is zero.

Question 19. What will be the total flux through the faces of the cube as given in the figure with side of length a if a charge q is placed at

(a) A a comer of the cube
(b) B mid-point of an edge of the cube (c) C centre of a face of the cube
(d) D mid-point of B and C
Solution: (a)Use of symmetry consideration may be useful in problems of flux calculation. We can imagine the charged particle is placed at the centre of a cube of side 2a. We can observe that the charge is being shared equally by
8 cubes. Therefore, total flux through the faces of the given cube =q/8ϵ₀

(b) If the charge q is placed at B, middle point of an edge of the cube, it is being shared equally by 4 cubes. Therefore, total flux through the faces
of the given cube = q/4ϵ₀

(c) If the charge q is placed at C, the centre of a face of the cube, it is being shared equally by 2 cubes. Therefore, total flux through the faces of the
given cube =q/2ϵ₀

(d) Finally, if charge q is placed at D, the mid-point of B and C, it is being shared equally by 2 cubes. Therefore, total flux through the faces of the
given cube =q/2ϵ₀

Short Answer Type Questions

Question 20. A paisa coin is made up of Al-Mg alloy and weight 0.75 g. It has a square shape and its diagonal measures 17 mm. It is electrically neutral and contains equal amounts of positive and negative charges.
Solution:

Question 21. Consider a coin of Question 20. ft is electrically neutral and contains equal amounts of positive and negative charge of magnitude 34.8 kC. Suppose that these equal charges were concentrated in two point charges separated by
(i) 1 cm — (1/2 x diagonal of the one paisa coin)
(ii) 100 m (~ length of a long building)
(iii) 106 m (radius of the earth). Find the force on each such point charge in each of the three cases. What do you conclude from these results?
Solution: We know force between two point charges separated at a distance r,

Conclusion: Here we can observe that when positive and negative charges in ordinary neutral matter are separated as point charges, they exert very large force. It means, it is very difficult to disturb electrical neutrality of matter.

Question 22. Figure represents a crystal unit of cesium chloride, CsCl. The cesium atohis, represented by open circles are situated at the comers of a cube of side 0.40 nm, whereas a Cl atom is situated at
the centre of the Cube.

The Cs atoms are deficient in one electron while the Cl atom carries an excess electron.
(i) What is the net electric field on the Cl atom due to eight Cs atoms?
(ii) Suppose that the Cs atom at the comer A is missing. What is the net force now on the Cl atom due to seven remaining Cs atoms?
Solution:
(i) The cesium atoms, are situated at the comers of a cube and Cl atom is situated at the centre of the cube. From the given figure, we can analyse that the chlorine atom is at equal distance from all the eight comers of cube where cesium atoms are placed. Thus, due to symmetry the electric field due to all Cs atoms, on Cl atom will cancel out. Hence net electric field at the centre of cube is zero.
(ii) We define force on a charge particle due to external electric field as F = qE. If eight cesium atoms, are situated at the comers of a cube, the net force on Cl atom is situated at the centre of the cube will be zero as net electric field at the centre of cube is zero. We can write that the vector sum of electric field due to charge A and electric field due to other seven charges at the centre of cube should be zero or, E_A + E_{seven charges}= 0

Question 23. Two charges q and -3q are placed fixed on x-axis separated by a distance d. Where should a third charge 2q be placed such that it will not experience any force?
Solution: The force on any charge will be zero only if net electric field at the position of charge is zero. Let electric field is zero at a distance x from charge q.

Question 24. Figure shows the electric field lines around three point charges A, B and C.

(i) Which charges are positive?
(ii) Which charge has the largest magnitude? Why?
(iii) In which region or regions of the picture could the electric field be zero? Justify your answer.
(a) Near A (b) Near B
(c) Near C (d) Nowhere
Solution:
Key concept:

• The number of lines originating or terminating on a charge is proportional to the magnitude of charge. In the following figure electric lines of force are originating from A and terminating at B, hence Q_A is positive while Q_B is negative. Also number of electric lines at force linked with Q_A are more than those linked with Q_B, hence |Q_A| > |Q_B|.
• The electric lines of forces always starts from a positive charge and ends at a negative charge. In case of a single isolated charge, electric lines of force start from positive charge ends at infinity. There is no neutral point between unlike charges. Point between two
like charges where electrostatic force is zero is called neutral point. A neutral point may exist between two like charges. Also between two like charges the neutral point is closer to the charge with smaller magnitude.
(i) Here, in the figure, the electric lines of force starts from A and C.
Therefore, charges A and C must be positive.
(i) The number of electric lines of forces starting from charge C are maximum, so C must have the largest magnitude.
(iii) From the figure we see that a neutral point exists between charges A and C. Here, more number of electric lines of forces shows higher strength of charge C than A. Thus, electric field is zero near charge A hence neutral point lies near A.

Question 25. Five charges, q each are placed at the comers of a regular pentagon of side a.

(a) (i) What will be the electric field at O,
the centre of the pentagon?
(ii) What will be the electric field at O if the charge from one of the comers (say A) is removed?
(iii) What will be the electric field at O if the charge q at A is replaced by – q?
(b) How would your answer to (a) be affected if pentagon is replaced by n-sided regular polygon with charge q at each of its comers?
Solution: (a)
(i) The point O, the centre of the pentagon is equidistant from all the charges at the end point of pentagon. Thus, due to symmetry, the electric field due to all the charges are cancelled out. As a result electric field at O is zero.
(ii) We can write that the vector sum of electric field due to charge A and electric field due to other four charges at the centre of cube should be zero or,

(b) If pentagon is replaced by n-sided regular polygon with charge q at each of its comers. Here again charges are symmetrical about the centre. The net electric field at O would continue to be zero, it doesn’t depend on the number of sides or the number of charges.

Long Answer Type Questions

Question 26. In 1959 Lyttleton and Bondi suggested that the expansion of the universe could be explained if matter carried a net charge. Suppose that the universe is made up of hydrogen atoms with a number density N, which is maintained a constant. Let the charge on the proton be e_p = -(1 + y)e where e is the electronic charge.
(a) Find the critical value of y such that expansion may start.
(b) Show that the velocity of expansion is proportional to the distance from the centre.
Solution: (a) Let the Universe have a radius R. Assume that the hydrogen atoms are uniformly distributed. The expansion of the universe will start if the coulomb repulsion on a hydrogen atom, at R is larger than the gravitational attraction.

Question 27. Consider a sphere of radius R with charge density distributed as p(r) = kr for r <= R
= 0 for r > R.
(a) Find the electric field at all points r.
(b) Suppose the total charge on the sphere is 2e where e is the electron charge. Where can two protons be embedded such that the force on each of them is zero. Assume that the introduction of the proton does not alter the negative charge distribution?
Solution: (a) The expression of charge density distribution in the sphere suggests that the electric field is radial.

Question 28.

Two fixed, identical conducting plates (a and P), each of surface area .S’ are charged to -Q and q, respectively, where Q > q >0. A third identical plate (j), free to move is located on the other side of the plate with charge q at a distance d (figure). The third plate is released and collides with the plate p. Assume the collision is elastic and the time of collision is sufficient to redistribute charge amongst p and y
(a) Find the electric field acting on the plate y before collision.
(b) Find the charges on P and yafter the collision.
(c) Find the velocity of the plate yafter the collision and at a distance d from the plate /?.
Solution:

Question 29. There is another useful system of units, besides the SI/MKS. A system, called the CGS (Centimeter-Gram-Second) system. In this system, Coulomb’s law
is given by F = (Q q/r²)r .

Solution:

Question 30.

Solution:

Question 31. Total charge -Q is uniformly spread along the length of a ring of radius R. A small test charge +q of mass m is kept at the centre of the ring and is given a gentle push along the axis of the ring.
(a) Show that the particle executes a simple harmonic oscillation.
(b) Obtain its time period.
Solution:

March 20, 2018
NCERT Exemplar Problems Solutions Mathematics Class 12th
NCERT Exemplar Problems Solutions class 12 maths download, Get all mathematics class 12th ncert exemplar solution with explanation. Step by Step Solution. This series of NCERT Exemplar Solutions for Class XII contains detailed explanations/solutions to all questions given in the NCERT Exemplar Class XII books. Detailed solutions/explanations have been given for the problems in order to make the students thoroughly understand the concept(s) involved in. Labeled illustrations/figures, tables, equations, in-text formulae, etc., have been provided, wherever required, for effective understanding of the concept(s).

NCERT Exemplar Problems Class 12 Mathematics
March 20, 2018
Probability NCERT Exemplar Problems Solutions Class 12th

NCERT Exemplar Problems Class 12 Mathematics Chapter 13 Probability

Short Answer Type Questions
1. For a loaded die, the probabilities of outcomes are given as under:
P(1) = P(2) = 0.2, P(3) = P(5) = P(6) = 0.1 and P(4) = 0.3.
The die is thrown two times. Let A and B be the events, ‘same number each time’, and ‘a total score is 10 or more’, respectively. Determine whether or not/l and B are independent.

2. Refer to Exercise 1 above. If the die were fair, determine whether or not the events A and B are independent.

4. A bag contains 5 red marbles and 3 black marbles. Three marbles are drawn one by one without replacement. What is the probability that at least one of the three marbles drawn be black, if the first marble is red?

5. Two dice are thrown together and the total score is noted. The events E, F and G are ‘a total of 4’, ‘a total of 9 or more’, and ‘a total divisible by 5’, respectively. Calculate P(E), P(F) and P(G) and decide which pairs of events, if any, are independent.

6. Explain why the experiment of tossing a coin three times is said to have binomial distribution.
Sol. We know that, in a Bindmial distribution,
(i) There are 2 outcomes for each trial
(ii) There is a fixed number of trials
(iii) The probability of success must be the same for all the trials.
When coin is tossed, possible outcomes are Head and Tail.
Since coin is tossed three times, we have fixed number of trials.
Also probability of Head and Tail in each trial is 1/2.
Thus given experiment is said to have binomial distribution.

12. If X is the number of tails in three tosses of a coin, determine the standard deviation of X.

13. In a dice game, a player pays a stake of Rs 1 for each throw of a die. She receives Rs 5 if the die shows a 3, Rs 2 if the die shows a 1 or 6, and nothing otherwise. What is the player’s expected profit per throw over a long series of throws?

14. Three dice are thrown at the same time. Find the probability of getting three two’s, if it is known that the sum of the numbers on the dice was six.

15. Suppose 10,000 tickets are sold in a lottery each for Rs 1. First prize is of Rs 3000 and the second prize is of Rs 2000. There are three third prizes of Rs.500 each. If you buy one ticket, what is your expectation?

16. A bag contains 4 white and 5 black balls. Another bag contains 9 white and 7 black balls. A ball is transferred from the first bag to the second and then a ball is drawn at random from the second bag. Find the probability that the ball drawn is white.

17. Bag I contains 3 black and 2 white balls, Bag II contains 2 black and 4 white balls. A bag and a ball is selected at random. Determine the probability of selecting a black ball.

18. A box has 5 blue and 4 red balls. One ball is drawn at random and not replaced. Its colour is also not noted. Then another ball is drawn at random. What is the probability of second ball being blue?

19. Four cards are successively drawn without replacement from a deck of 52 playing cards. What is the probability that all the four cards are kings?

20. A die is thrown 5 times. Find the probability that an odd number will come up exactly three times.

21. Ten coins are tossed. What is the probability of getting at least 8 heads?

22. The probability of a man hitting a target is 0.25. He shoots 7 times. What is the probability of his hitting at least twice?

23. A lot of 100 watches is known to have 10 defective watches. If 8 watches are selected (one by one with replacement) at random, what is the probability that there will be at least one defective watch?

31. A factory produces bulbs. The probability that any one bulb is defective is 1/50 and they are packed in boxes of 10. From a single box, find the probability that
(i) none of the bulbs is defective
(ii) exactly two bulbs are defective
(iii) more than 8 bulbs work properly

32. Suppose you have two coins which appear identical in your pocket. You know that one is fair and one is 2-headed. If you take one out, toss it and get a head, what is the probability that it was a fair coin?

33. Suppose that 6% of the people with blood group O are left handed and 10% of those with other blood groups are left handed. 30% of the people have blood group O. If a left handed person is selected at . random, what is the probability that he/she will have blood group O?

35. Find the probability distribution of the maximum of the two scores obtained when a die is thrown twice . Determine also the mean of the distribution.

38. A and B throw a pair of dice alternately. A wins the game if he gets a total of 6 and B wins if she gets a total of 7. If A starts the game, find the probability of winning the game by A in third throw of the pair of dice.

40. An um contains m white and n black balls. A ball is drawn at random and is put back into the um along with k additional balls of the same colour as that of the ball drawn. A ball is again drawn at random. Show that the probability of drawing a white ball now does not depend on k.

Long Answer Type Questions

43. A shopkeeper sells three types of flower seeds A₁,A₂ and A₃. They are sold as a mixture where the proportions are 4:4:2 respectively. The germination rates of the three types of seeds are 45%, 60% and 35%. Calculate the probability
(i) of a randomly chosen seed to germinate
(ii) that it will not germinate given that the seed is of type A₃,
(iii) that it is of the type A₂ given that a randomly chosen seed does not germinate.

44. A letter is known to have come either from TATA NAGAR or from CALCUTTA. On the envelope, just two consecutive letter TA are visible. What is the probability that the letter came from TATA NAGAR.
Sol. Let Ex be the event that letter is from TATA NAGAR and E2 be the event that letter is from CALCUTTA.

45. There are two bags, one of which contains 3 black and 4 white balls while the other contains 4 black and 3 white balls. A die is thrown. If it shows up 1 or 3, a ball is taken from the 1st bag; but it shows up any other number, a ball is chosen from the second bag. Find the probability of choosing a black ball.

46. There are three urns containing 2 white and 3 black balls, 3 white and 2 black balls, and 4 white and 1 black balls, respectively. There is an equal probability of each urn being chosen. A ball is drawn at random from the chosen urn and it is found to be white. Find the probability that the ball drawn was from the second urn.

47. By examining the chest X ray, the probability that TB is detected when a person is actually suffering is 0.99. The probability of ah healthy person diagnosed to have TB is 0.001. In a certain city, 1 in 1000 people suffers from TB. A person is selected at random and is diagnosed to have TB. What is the probability that he actually has TB?

48. An item is manufactured by three machines A, B and C. Out of the total number of items manufactured during a specified period, 50% are manufactured on A, 30% on B and 20% on C. 2% of the items produced on A and 2% of items produced on B are defective, and 3% of these produced on C are defective. All the items are stored at one go down. One item is drawn at random and is found to be defective. What is the probability that it was manufactured on machine A?
Sol. Let E₁, E₂, E₃ be the event that item is manufactured on A,B and C respectively. Let E be the event that an item is defective.

=> 124n + 62 = 126n + 42
=> 2n = 20=>n=10
53. Two cards are drawn successively without replacement from a well shuffled deck of cards. Find the mean and standard variation of the random variable X where X is the number of aces.

54. A die is tossed twice. A ‘success’ is getting an even number on a toss. Find the variance of the number of successes.

55. There are 5 cards numbered 1 to 5, one number on one card. Two cards are drawn at random without replacement. Let X denote the sum of the numbers on two cards drawn. Find the mean and variance of X.

Objective Type Questions

70. If two events are independent, then
(a) they must be mutually exclusive
(b) the sum of their probabilities must be equal to 1
(c) (A) and (B) both are correct
(d) None of the above is correct
Sol. (d) If two events A and B are independent, then we know that

If A and B are independent, knowledge that A occurred does not change the probabilities that B may have occurred. Whereas if A and B are disjoint, knowledge that A occurred completely changes the probabilities that B may have occurred by collapsing it to 0.

77. Assume that in a family, each child is equally likely to be a boy or a girl. A family with three children is chosen at random. The probability that the eldest child is a girl given that the family has at least one girl is

True/False Type Questions

Fill in the Blanks Type Questions

March 20, 2018
Linear Programming NCERT Exemplar Problems Solutions Class 12th

NCERT Exemplar Problems Class 12 Mathematics Chapter 12 Linear Programming

Short Answer Type Questions

4. Minimize Z = 13x- 15y subject to the constraints: x+y≤ 7,2x-3y + 6 ≥ 0, x ≥ 0, y ≥ 0.
Sol. We have to Minimize Z = 13x – 15y subject to the constraints x + y ≤7, 2x – 3y + 6 ≥ 0, x ≥ 0, y ≥ 0. These inequalities are plotted as shown in the following figure.

8. Refer to Exercise 7 above. Find the maximum value of Z.
Sol. Z is maximum at (3,2) and its maximum value is 47.

9. The feasible region for a LPP is shown in the following figure. Evaluate Z = 4x+y at each of the comer points of this region. Find the minimum value of Z, if it exists.

Now, we see that 3 is the smallest value of Z the comer point (0, 3). Note that here we see that, the region is unbounded, therefore 3 may not be the minimum value of Z. To decide this issue, we graph the inequality 4x + y < 3 and check whether the resulting open half plane has no point in common with feasible region otherwise, Z has no minimum value.
From the shown graph above, it is clear that there is no point in common with feasible region and hence Z has minimum value 3 at (0, 3).

10. In the following figure, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of Z = x + 2y

11. A manufacturer of electronic circuits has a stock of 200 resistors, 120 transistors and 150 capacitors and is required to produce two types of circuits A and B. Type A requires 20 resistors, 10 transistors and 10 capacitors. Type B requires 10 resistors, 20 transistors and 30 capacitors. If the profit on type A circuit is Rs 50 and that on type B circuit is Rs 60, formulate this problem as a LPP so that the manufacturer can maximise his profit.
Sol. Let the manufacture produces x units of type A circuits and y units of type B circuits. Form the given information, we have following corresponding constraint table.

12. A firm has to transport 1200 packages using large vans which can carry 200 packages each and small vans which can take 80 packages each. The cost for engaging each large van is Rs 400 and each small van is Rs 200. Not more than Rs 3000 is to be spent on the job and the number of large vans can not exceed the number of small vans. Formulate this problem as a LPP given that the objective is to minimise cost.
Sol. Let the firm has x number of large vans and y number of small vans.
From the given information, we have following corresponding constraint table.

13. A company manufactures two types of screws A and B. All the screws have to pass through a threading machine and a slotting machine. A box of Type A screws requires 2 minutes on the threading machine and 3 minutes on the slotting machine. A box of type B screws requires 8 minutes of threading on the threading machine and 2 minutes on the slotting machine. In a week, each machine is available for 60 hours. On selling these screws, the company gets a profit of Rs 100 per box on type A screws and Rs 170 per box on type B screws. Formulate this problem as a LPP given that the objective is to maximise profit.
Sol. Let the company manufactures x boxes of type A screws and y boxes of type B screws.
From the given information, we have following corresponding constraint table.

14. A company manufactures two types of sweaters: type A and type B. It costs Rs 360 to make a type A sweater and Rs 120 to make a type B sweater. The company can make at most 300 sweaters and spend at most Rs 72000 a day. The number of sweaters of type B cannot exceed the number of sweaters of type A by more than 100. The company makes a profit of Rs 200 for each sweater of type A and ?120 for every sweater of type B. Formulate this problem as a LPP to maximise the profit to the company.
Sol. Let the company manufactures x number of type A sweaters and y number of type B.
The company spend at most Rs 72000 a day.
∴ 360x + 120y ≤ 72000
=> 3x+y≤ 600 …(i)
Also, company can make at most 300 sweaters.
∴ x+y≤ 300 …(ii)
Also, the number of sweaters of type B cannot exceed the number of sweaters of type A by more than 100 i.e., y-x≤ 100
The company makes a profit of Rs 200 for each sweater of type A and Rs 120 for every sweater of type B
So, the objective function for maximum profit is Z = 200x + 120y subject to constraints.
3x+y≤ 600
x+y ≤ 300
x-y ≥ -100
x ≥ 0, y ≥ 0

15. A,man rides his motorcycle at the speed of 50 km/hour. He has to spend Rs 2 per km on petrol. If he rides it at a faster speed of 80 km/hour, the petrol cost increases to Rs 3 per km. He has atmost Rs120 to spend on petrol and one hour’s time. He wishes to find the maximum distance that he can travel. Express this problem as a linear programming problem.
Sol. Let the man rides to his motorcycle to a distance x km at the speed of 50 km/h and to a distance y km at the speed of 80 km/h.
Therefore, cost on petrol is 2x + 3y.
Since, he has to spend Rs120 atmost on petrol.
∴ 2x + 3y ≤ 120 …(i)
Also, he has at most one hour’s time.

Long Answer Type Questions
16. Refer to Exercise 11. How many of circuits of Type A and of Type B, should be produced by the manufacturer so as to maximize his profit? Determine the maximum profit.

22. A manufacturer produces two Models of bikes’-Model X and Model Y. Model X takes a 6 man-hours to make per unit, while Model Y takes 10 man-hours per unit. There is a total of 450 man-hour available per week. Handling and Marketing costs are Rs 2000 and Rs 1000 per unit for Models X and Y respectively. The total funds available for these purposes are Rs 80,000 per week. Profits per unit for Models X and Y are Rs 1000 and Rs 500, respectively. How many bikes of each model should the manufacturer produce so as to yield a maximum profit? Find the maximum profit.

So, for maximum profit manufacture must produces 25 number of models X and 30 number of model Y bikes.

23. In order to supplement daily diet, a person wishes to take some X and some Y tablets. The contents of iron, calcium and vitamins in X and Y (in milligrams per tablet) are given as below:

The person needs at least 18 milligrams of iron, 21 milligrams of calcium and 16 milligram of vitamins. The price of each tablet of X and Y is Rs 2 and Rs 1 respectively. How many tablets of each should the person take in order to satisfy the above requirement at the minimum cost?

From the figure, we can see the feasible region is unbounded region, with comer points as A(%, 0), B(6,1), C(I, 6), and D(0, 9)

Thus, the minimum value of Z is ‘8’ occurring at B( 1, 6). Since the feasible region is unbounded, ‘8’ may not be the minimum value of Z. To decide this, we plot the inequality 2x+y < 8 and check whether the resulting open half has points common with feasible region or not If it has common point, then 8 will not be the minimum value of Z, otherwise 8 will be the minimum value of Z. Thus, from the graph it is clear that, it has no common point.
Therefore, Z= 2x+y-has 8 as minimum value subject to the given constrains. Hence, the person should take 1 unit of X tablet and 6 units of Y tablets to satisfy the given requirements and at the minimum cost of Rs 8.

24. A company makes 3 models of calculators: A, B and C at factory I and factory II. The company has orders for at least 6400 calculators of model A, 4000 calculator of model B and 4800 calculator of model C. At factory I, 50 calculators of model A, 50 of model B and 30 of model C are made every day; at factory II, 40 calculators of model A, 20 of model B and 40 of model C are made everyday. It costs Rs 12000 and Rs 15000 each day to operate factory I and II, respectively. Find the number of days each factory should operate to minimize the operating costs and still meet the demand.

Objective Type Questions
26. The comer points of the feasible region determined by the system of linear constraints are (0,0), (0,40), (20,40), (60,20), (60,0). The objective function is Z=4x + 3y.
Compare the quantity in Column A and Column B
Column A Column B
Maximum of Z 325
(a) The quantity in column A is greater
(b) The quantity in column B is greater
(c) The two quantities are equal
(d) The relationship can not be determined on the basis of the information supplied .
Sol. (b)

28. Refer to Exercise 27. Maximum of Z occurs at
(a) (5,0) (b) (6,5) (c) (6, 8) (d) (4, 10)
Sol. (a) Refer to solution 27, maximum of Z occurs at (5, 0)
29. Refer to Exercise 27. (Maximum value of Z + Minimum value of Z) is equal to
(a) 13 (b) 1 (c) -13
Sol. (d) Refer to solution 27,
maximum value of Z + minimum value of Z = 15-32 = -17

31. Refer to Exercise 30. Minimum value of F is
(a) 0 (b) -16 . (c) 12 (d) does not exist
Sol. (b) Referring to solution 30, minimum value of F is -16 at (0,4).

32. Comer points of the feasible region for an LPP are (0, 2), (3, 0), (6,0), (6, 8) and (0,5).
Let F = 4x + 6y be the objective function.
The Minimum value of F occurs at
(a) (0,2) only
(b) (3,0) only
(c) the mid point of the line segment joining the points (0,2) and (3,0) only
(d) any point on the line segment joining the points (0,2) and (3, 0).
Sol. (d)

33. Refer to Exercise 32, Maximum of F – Minimum of F=
(a) 60 (b) 48 (c) 42 (d) 18
Sol. (a) Referring to the solution 32, maximum,of F-minimum of F= 72- 12 = 60

34. Comer points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px + qy, where p,q>0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1,1) is
(a) p = 2q (b )P=q\2 (c)p = 3q (d) p = q
Sol. (b)

Fill in the Blanks Type Questions
35. In a LPP, the linear inequalities or restrictions on the variables are called————-.
Sol. In a LPP, the linear inequalities or restrictions on the variables are called linear constraints.

36. In a LPP, the objective function is always————.
Sol. In a LPP, objective function is always linear.

37. If the feasible region for a LPP is————, then the optimal value of the objective function Z= axH-fiy may or may not exist.
Sol. If the feasible region for a LPP is unbounded, then the optimal value of the objective function Z = ax + by may or may not exist.

38. In a LPP if the objective function Z=ax+ by has the same maximum value on two comer points of the feasible region, then every point on the line segment joining these two points give the same————value.
Sol. In a LPP, if the objective function Z = ax + by has the same maximum value on two comer points of the feasible region, then every point on the line segment joining these two points gives the same maximum value.

39. A feasible region of a system of linear inequalities is said to be————if it can be enclosed within a circle.
Sol. A feasible region of a system of linear inequalities is said to be bounded, if it can be enclosed within a circle.

40. A comer point of a feasible region is a point in the region which is the———— of two boundary lines.
Sol. A comer point of a feasible region is a point in the region which is the intersection of two boundary lines.

41. The feasible region for an LPP is always a————polygon.
Sol. The feasible region for an LPP is always a convex polygon.

True/False Type Questions
42. If the feasible region for a LPP is unbounded, maximum or minimum of the objective function Z = ax+ by may or may not exist.
Sol. True

43. Maximum value of the objective function Z = ax+ by in a LPP always occurs
at only one comer point of the feasible region. ,
Sol. False

44. In a LPP, the minimum value of the objective function Z = ax+ by is always 0 if origin is one of the comer point of the feasible region.
Sol. False

45. In a LPP, the maximum value of the objective function Z = ax+ by is always finite.
Sol. True

March 20, 2018
Three Dimensional Geometry NCERT Exemplar Problems Solutions Class 12th

NCERT Exemplar Problems Class 12 Mathematics Chapter 11 Three Dimensional Geometry

Short Answer Type Questions

5. Prove that the line through A(0, -1, -1) and B(4, 5, 1) intersects the line through C(3, 9,4) and D(- 4,4,4).
Sol. We know that, the equation of a line that passes through two points (x₁, y₁, z₁) and (x₂, y₂, z₂) is

7. Find the equation of a plane which bisects perpendicularly the line joining the points A(2, 3,4) and 5(4, 5, 8) at right angles.

8. Find the equation of a plane which is at a distance 3 √3 units from origin and the normal to which is equally inclined to coordinate axis.

9. If the line drawn from the point (-2, -1,-3) meets a plane at right angle at the point (1, -3, 3), find the equation of the plane.
Sol. Since, the line drawn from the point B(-2, -1,-3) meets a plane a plane at right angle at the point 4(1,-3, 3).
So, the plane passes through the point 4(1, -3, 3)

10. Find the equation of the plane through the points (2, 1, 0), (3, -2, -2) and (3, 1, 7).
Sol. We know that, the equation of a plane passing through three non-collinear points (x1. y1, z1), (x₂, y₂, z₂) and (x₃, y₃, z₃) is

14. O is the origin and A is (a, b, c). Find the direction cosines of the line OA and the equation of plane through A at right angle to OA.

Long Answer Type Questions

19. Find the equations of the line passing through the point (3,0,1) and parallel to the planes x + 2y = 0 and 3y-z = 0.

20. Find the equation of the plane through the points (2,1, -1) and (-1,3,4), and perpendicular to the plane x-2y + 4z = 10.

22. Find the equation of the plane which is perpendicular to the plane 5x + 3y + 6z + 8 = 0 and which contains the line of intersection of the planes x + 2y + 3z – 4 = 0 and 2x + y- z + 5 = 0.

27. Show that the straight lines whose direction cosines are given by 2l+2m -n=0 and mn + nl + lm = 0 are at right angles.

Objective Type Questions

30. If the directions cosines of a line are k, k, ‘k, then

33. The reflection of the point (α, β,γ) in the xy-plane is
(a) (α, β,0) (b) (0,0, γ) (c) (-α, -β, γ) (d) (α, β,-γ)
Sol. (d) In xy-plane, the reflection of the point (α, β,γ) is (α, β,-γ)
34. The area of the quadrilateral ABCD, where A(0,4,1), B(2, 3, -1), C(4, 5, 0) and D(2, 6,2) is equal to
(a) 9 sq. units (b) 18 sq. units (c) 27 sq. units (d) 81 sq. units

35. The locus represented by xy + yz = 0 is
(a) A pair of perpendicular lines (b) A pair of parallel lines
(c) A pair of parallel planes (d) A pair of perpendicular planes

Fill in the Blanks Type Questions

True/False Type Questions

March 20, 2018
Vector Algebra NCERT Exemplar Problems Solutions Class 12th

NCERT Exemplar Problems Class 12 Mathematics Chapter 10 Vector Algebra

Short Answer Type Questions

3. Find a unit vector in the direction of PQ, where P and Q have co-ordinates (5,0, 8) and (3, 3,2), respectively.

5. Using vectors, find the value of k such that the points (k, -10, 3), (1, -1, 3) and (3, 5, 3) are collinear.

13. Using vectors, find the area of the triangle ABC with vertices A(l, 2, 3), 5(2, -1, 4) and C(4,5,-l).

14. Using vectors, prove that the parallelogram on the same base and between the same parallels are equal in area.

Long Answer Type Questions

Objective Type Questions

Fill in the Blanks Type Questions

True/False Type Questions

42. Position vector of a point P is a vector whose initial point is origin.

March 20, 2018
Differential Equations NCERT Exemplar Problems Solutions Class 12th

NCERT Exemplar Problems Class 12 Mathematics Chapter 9 Differential Equations

Short Answer Type Questions

2. Find the differential equation of all non-vertical lines in a plane.

13. Form the differential equation having y = (sin^-1 x)²+ A cos^-1 x + B, where A and B are arbitrary constants, as its general solution.

14. Form the differential equation* of all circles which pass through origin and whose centres lie on y-axis.

19. Solve : (x + y)(dx -dy) = dx + dy
[Hint: Substitute x+y = z after separating dx and dy]

21. Solve the differential equation dy = cos x (2 – y cosec x) dx given that y=2 when x = π /2.

22. Form the differential equation by eliminating A and B in Ax² -By² = 1.

23. Solve the differential equation (1 +y²) tan^-1 x dx + 2y (1+x²)dy=0.

24. Find the differential equation of system of concentric circles with centre (1,2).

Long Answer Type Questions

31. Find the equation of a curve passing through origin if the slope of the tangent to the curve at any point (x, y) is equal to the square of the difference of the abscissa and ordinate of the point.

32. Find the equation of a curve passing through the point (1, 1). If the tangent drawn at any point P(x, y) on the curve meets the co-ordinate axes at A and B such that P is the mid-point of AB.

Objective Type Questions

60. Family y = Ax + A3 of curves will correspond to a differential equation of order ,
(a) 3 (b) 2 (c) 1 (d) not defined

62. The curve for which the slope of the tangent at any point is equal to the ratio of the abscissa to the ordinate of the point is
(a) an ellipse (b) parabola
(c) circle (d) rectangular hyperbola

Fill in the Blanks Type Questions

True/False Type Questions

March 20, 2018
Applications of Integrals NCERT Exemplar Problems Solutions Class 12th

NCERT Exemplar Problems Class 12 Mathematics Chapter 8 Applications of Integrals

Short Answer Type Questions

Long Answer Type Questions

Objective Type Questions

March 20, 2018
Integrals NCERT Exemplar Problems Solutions Class 12th

NCERT Exemplar Problems Class 12 Mathematics Chapter 7 Integrals

Short Answer Type Questions

Long Answer Type Questions

Objective Type Questions

Fill In the Blanks Type Questions

March 20, 2018