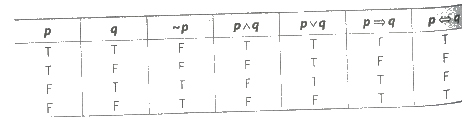
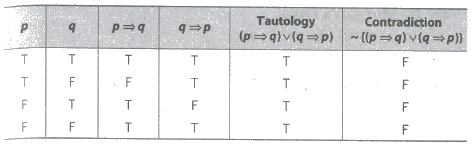
MULTIPLE CHOICE QUESTIONS (1 MARK)
Q.1. Indian Standard Time or I.S.T. is how many hours ahead or behind of G.M.T. or Universal Time?
(a) 5 hrs 30 min behind GM.T. (b) 15 hrs ahead of G.M.T.
(c) 5 hrs 30 min ahead of GM.T. (d) None of the above
Ans. (c)
Q.2. Which of the following has reduced India’s distance from Europe by 7000 km?
(a) Suez Canal (b) Panama Canal
(c) Indira Gandhi Canal (d) Buckingham Canal
Ans. (a)
Q.3. Which of the following influences the duration of the day and night, as one moves from south to north?
(a) Longitudinal extent (b) Latitudinal extent
(c) Standard Meridian (d) All the above
Ans. (b)
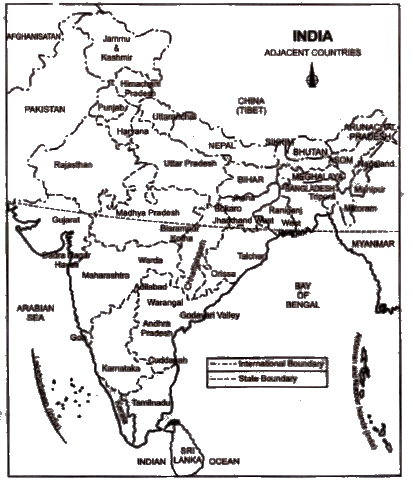
Q.4. The Standard Meridian of India, 82°30’E passes through which of the following places?
(a) Kanniyakumari in Tamil Nadu (b) Walong in Arunachal Pradesh
(c) Kachchh in Gujarat (d) Mirzapur in Uttar Pradesh
Ans. (d)
Q.5. The sun rises two hours earlier in Arunachal Pradesh as compared to Gujarat. What time will the watch show in Gujarat if it is 6 am in Arunachal Pradesh? [Important]Q.5. The sun rises two hours earlier in Arunachal Pradesh as compared to Gujarat. What time will the watch show in Gujarat if it is 6 am in Arunachal Pradesh? [Important]
(a) 4.16 am (b) 7.44 am (c) 6 am (d) 5.44 am
Ans. (c)
Q.6. If the local time at Dwarka (69°01’E) in Gujarat to the west of India is 6 am, what will be the local time at Dibrugarh (94°58’E approximately 95°), in Assam, in the east?
[Important]
(a) 4.16 am (b) 6 am (c) 7.44 am (d) 7.44 pm
Ans. (c)
Q.7. From Arunachal Pradesh to Gujarat there is a time lag of :
(a) 24 hours (b) 12 hours (c) 2 hours (d) 30 minutes
Ans. (c)
Q.8. Both the latitudinal and longitudinal extent of India’s mainland is about 30°. But on looking at the map of India which of the following alternatives do you observe about India’s size? [Important]
(a) East-west extent appears to be smaller than north-south extent
(b) East-west extent appears to be larger than north-south extent
(c) East-west and north-south extent appears equal
(d) North-south extent appears to be smaller than east-west extent Ans. (a)
Q.9. Approximately what is the latitudinal and longitudinal extent of the mainland of India?
[Important]
(a) 97° (b) 68° (c) 30° (d) 8°
Ans. (c)
Q.10. Which geographical feature bounds India’s mainland south of 22°N latitude?
(a) Young Fold Mountains (b) Sandy Desert
(c) Lava Plateaus (d) Seas and Ocean
Ans. (d)
Q.11. By which geographical feature is India bounded in the north-west, north and north-east?
(a) Seas (b) Lave Plateaus
(c) Young Fold Mountains (d) Sandy Desert
Ans. (c)
Q.12. What is India’s size with respect to other countries of the world?
(a) First (b) Third (c) Fourth (d) Seventh
Ans. (d)
Q.13. Which of the following figures shows the total area of India’s landmass?
(a) 2.4 million square km (b) 3.28 million square km
(c) 32.8 million square km (d) 3.28 million km
Ans. (b)
Q.14. Which of the following groups of islands belonging to the Indian territory lies in the Arabian Sea?
(a) Andaman and Nicobar Islands (b) Sri Lanka
(c) Lakshdweep (d) Maldives
Ans. (c)
Q.15. Which of the following groups of islands belonging to the Indian territory lies in the Bay of Bengal?Q.15. Which of the following groups of islands belonging to the Indian territory lies in the Bay of Bengal?
(a) Andaman and Nicobar Islands (b) Sri Lanka
(c) Lakshadweep (d) Maldives
Ans. (a)
Q.16. Which latitude passes through the southern-most point of India’s mainland?
(a) 8°4/N (b) 37°6/N (c) 8°4’S (d) 82°30’E
Ans. (a)
Q.17. Which of the following is the western-most longitude of India?
(a) 97°25’E (b) 68°7’E (c) 68°7’E (d) 82°32’E
Ans. (b)
Q.18. The eastern-most longitude of India is _
(a) 97°25’E (b) 68°7’E (c) 77°6’E (d) 82°32’E
Ans. (a)
Q.19. Which of the following parallels of latitude divides India into two almost equal parts?
(a) Equator (b) Tropic of Capricorn
(c) Tropic of Cancer (d) Prime Meridian
Ans. (c)
Q.20. Which of the following is the longitudinal extent of India?
(a) 8°4/N and 37°6/N (b) 68°7/N and 97°25’E
(c) 68°7’E and 97°25/W (d) 8°4’E and 37°6’E
Ans. (b)
Q.21. Which of the following places of India is located on the three seas? [Important]
(a) Port Blair (b) Kavaratti
(c) Kanniyakumari (d) Kochi
Ans. (c)
Q.22. India achieved multi-faceted socio-economic progress during which of the following periods?
(a) Since ancient times (b) During medieval period
(c) In the 21st century (d) During the last five decades
Ans. (d)
Q.23. Which of the following Union Territories is located along the west coast of India?
(a) Andaman and Nicobar Islands (b) Chandigarh
(c) Dadra and Nagar Haveli (d) Puducherry
Ans. (c)
Q.24. How many states and Union Territories are there in India?
(a) 28 states and 7 Union Territories including Delhi
(b) 23 States and 12 Union Territories
(c) 26 states and 9 Union Territories
(d) 30 States and 5 Union Territories
Ans. (a)
Q.25. Which of the following ports of India is closest to the Suez Canal route?Q.25. Which of the following ports of India is closest to the Suez Canal route?
(a) Kolkata (b) Chennai (c) Kochi (d) Mumbai
Ans. (d)
Q.26. Which of the following is the oldest route of contact between India and other countries of the world?
(a) Ocean routes (b) Maritime contact (c) Land routes (d) Air routes
Ans. (c)
Q.27. Due to which of the following reasons is the Indian Ocean named after India?
(a) India has a strategic location along the trans-Indian Ocean routes
(b) No other country has a long coastline on the Indian Ocean as India
(c) India is centrally located at the head of the Indian Ocean
(d) All the above Ans. (d)
Q.28. Which of the following longitudes is selected as the Standard Meridian for India?
(CBSE 2010)
(a) 68°7’E (b) 82°30’E (c) 97°25’E (d) 23°30/N
Ans. (b)
Q.29. In which of the following places, would you find the least difference in the duration between day time and night time?
(a) Kanniyakumari (b) Leh (b) Srinagar (d) Itanagar
Ans. (a)
Q.30. Tropic of Cancer passes through which of these states [2010 (T-1)]
(a) Orissa (b) Tripura (c) Bihar (d) Punjab
Ans. (b)
Q.31. Which one of the following is the southern-most Latitude of India? [2010 (T-1)]
(a) 8° 4′ North (b) 8° 4′ South (c) 6° 4′ South (d) 6° 4′ North
Ans. (c)
Q.32. The latitudinal extent of India lies between [2010 (T-1)]
(a) 7° 5′ N and 26° 5′ N (b) 8° 4′ N and 37° 6′ N
(c) 12° 5′ N and 27° 5′ N (d) 12° 5′ N and 37° 6′ N
Ans. (b)
Q.33. The Tropic of Cancer does not pass through [2010 (T-1)]
(a) Rajasthan (b) Tripura (c) Jharkhand (d) Bihar
Ans. (d)
Q.34. Which meridian is fixed as a Standard Meridian of India? [2010 (T-1)]
(a) 82/° E (b) 84/° E (c) 86° E (d) 81° E
Ans. (a)
Q.35. The easternmost longitude of India is : [2010 (T-1)]
(a) 97° 25′ E (b) 77° 6′ E (c) 68° 7′ E (d) 82° 32′ E
Ans. (a)
Q.36. What is the position of India in the world in respect of area? [2010 (T-1)]Q.36. What is the position of India in the world in respect of area? [2010 (T-1)]
(a) 8th position (b) 7th position (c) 6th position (d) 2nd position
Ans. (b)
Q.37. Which one of the following forms the southern-most tip of the Indian mainland?
[2010 (T-1)]
(a) Indira Point (b) Kanniyakumari (c) Palk Strait (d) Kavaratti
Ans. (b)
Q.38. Which line divides India into approximately two equal parts? [2010 (T-1)]
(a) Equator (b) Tropic of Cancer
(c) Tropic of Capricorn (d) None of these
Ans. (b)
Q.39. Which country among the India’s neighbours is the smallest? [2010 (T-1)]
(a) Nepal (b) Bhutan (c) Sri Lanka (d) Bangladesh
Ans. (b)
Q.40. How many states and Union Territories does India have? [2010 (T-1)]
(a) India has 26 States and 7 Union Territories
(b) India has 25 States and 7 Union Territories
(c) India has 28 States and 7 Union Territories
(d) India has 28 States and 6 Union Territories
Ans. (c)
Q.41. India’s total area accounts for what percentage of the geographical area of the world?
[2010 (T-1)]
(a) 2.9% (b) 3.2% (c) 2.4% (d) 4.2%
Ans. (c)
Q.42. Which one of the following routes are the oldest and provided India relationships with other countries? [2010 (T-1)]
(a) Land routes (b) Sea routes (c) Air routes (d) Rail routes
Ans. (a)
Q.43. India has land boundary of about [2010 (T-1)]
(a) 18,200 km (b) 7516.6 km (c) 15,200 km (d) 2458 km
Ans. (c)
Q.44. Which one of the following straits separates India from Sri Lanka? [2010 (T-1)]
(a) Sunda Strait (b) Johor Strait (c) Bering Strait (d) Palk Strait
Ans. (d)
Q.45. Which neighbouring country would you reach if you were to sail across the Palk Strait?
[2010 (T-1)]
(a) Myanmar (b) Maldives (c) Bangladesh (d) Sri Lanka
Ans. (d)
Q.46. The neighbouring countries that share their boundaries with India are : [2010 (T-1)]
(a) Pakistan and Afghanistan (b) Myanmar and Bangladesh
(c) China and Nepal (d) All the above
Ans. (d)
Q.47. Which one of the following Indian states does not share its boundary with Pakistan?Q.47. Which one of the following Indian states does not share its boundary with Pakistan?
[2010 (T-1)]
(a) Jammu and Kashmir (b) Rajasthan
(c) Gujarat (d) Haryana
Ans. (d)
Q.48. A narrow channel of sea separating two land-masses is called : [2010 (T-1)]
(a) Gulf (b) Strait (c) Isthmus (d) Bay
Ans. (b)
Q.49. The western-most Union Territory of India is [2010 (T-1)]
(a) Lakshwadeep (b) Daman and Diu (c) Puducherry (d) Dadar and Nagar Haveli Ans. (b)
Q.50. Which of the following states does not share any international boundary? [2010 (T-1)]
(a) Rajasthan (b) West Bengal (c) Uttarakhand (d) Madhya Pradesh
Ans. (d)
Q.51. The four states which are situated along the Himalayas are : [2010 (T-1)]
(a) Jammu and Kashmir, Himachal Pradesh, Uttarakhand, Arunachal Pradesh
(b) Gujarat, Maharashtra, Haryana, Rajasthan
(c) Gujarat, Chhattisgarh, Bihar, Jharkhand
(d) Bihar, West Bengal, Orissa, Uttar Pradesh Ans. (a)
Q.52. What is the length of Indian coastline? [2010 (T-1)]
(a) 8716 km (b) 7165 km (c) 9515 km (d) 7516 km
Ans. (d)
Q.53. Which of these countries do not share land borders with India? [2010 (T-1)]
(a) Russia (b) Bhutan (c) Myanmar (d) Pakistan
Ans. (a)
Q.54. Which one of the following water bodies separate Sri Lanka from India? [2010 (T-1)]
(a) Palk Strait and Gulf of Khambhat (b) Palk Strait and Gulf of Mannar
(c) Gulf of Mannar and 10° Channel (d) 10° Channel and Gulf of Khambhat
Ans. (b)